1．要使一个质量为3 kg的物体，在半径为2 m的圆周上以4 m/s的速度做匀速圆周运动，物体的向心加速度和所需向心力是多少？

【答案】

a＝8 m/s²，F＝24 N

 

2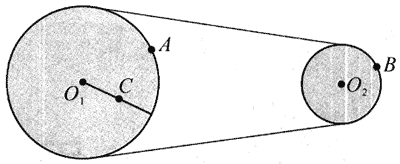．图中O₁、O₂两轮通过皮带传动，两轮半径之比r₁∶r₂＝2∶1，点A在O₁轮边缘上，点C在O₁轮半径中点，点B在O₂轮边缘上，请填写A、B、C三点的线速度之比、角速度之比和加速度之比。

（1）线速度之比：v_A∶v_B∶v_C＝__________。

（2）角速度之比：ω_A∶ω_B∶ω_C＝__________。

（3）加速度之比：a_A∶a_B∶a_C＝__________。

【答案】

（1）2∶2∶1

（2）1∶2∶1

（3）2∶4∶1

 

3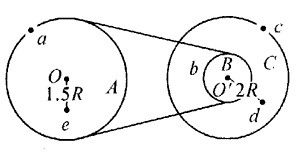．如图所示，一个大轮A通过皮带带动小轮B一起转动，小轮B与另一大轮C为同轴轮轴，假设皮带和A轮、B轮之间没有滑动，R_A＝R_C＝3R_B＝3R，a、b、c分别为A、B、C三个轮边缘上的点，C轮上的d点离转轴Oʹ的距离为R_d＝2R，A轮上的e点离转轴O的距离为R_e＝1.5R。求a、b、c、d、e五点的 ：

（1）线速度之比；

（2）角速度之比；

（3）向心加速度之比。

【答案】

（1）2∶2∶6∶4∶1

（2）1∶3∶3∶3∶1

（3）2∶6∶18∶12∶1

【解析】

在传动装置中，与皮带接触的各点具有相同的线速度，可知v_a＝v_b，而同轴轮上的各点具有相同的角速度可知ω_a＝ω_c，ω_b＝ω_c＝ω_d，利用这些特点，即可求解。

（1）由v_a∶v_e＝ω_A·3R∶ω_A·1.5R＝2∶1；

由v_b∶v_c∶v_d＝ω_BR∶ω_B·3R∶ω_B·2R＝1∶3∶2，因为v_a＝v_b，可知v_a∶v_b＝1∶1；

最后可得v_a∶v_b∶v_c∶v_d∶v_e＝2∶2∶6∶4∶1。

（2）由v_a＝v_b，得ω_a·3R＝ω_b·R，ω_a∶ω_b＝1∶3，因为ω_a＝ω_e以及ω_b＝ω_c＝ω_d，

可得

ω_a∶ω_b∶ω_c∶ω_d∶ω_e＝1∶3∶3∶3∶1。

（3）a_a∶a_b∶a_c∶a_d∶a_e＝ω_A²·3R∶ω_B²·R∶ω_B²·3R∶ω_B²·2R∶ω_A²·1.5R＝2∶6∶18∶12∶1。

 

4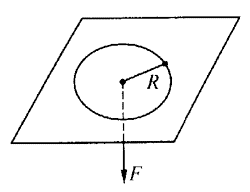．光滑水平板中央有一个无摩擦小孔，用一轻细绳一端拴一小球，另一端穿过小孔被力F拉着，使小球在板上做匀速圆周运动，轨道半径为R，如图所示。逐渐加大拉力，使球运动的半径逐渐减小，当拉力逐渐增大到8F，球运动的轨道半径逐渐减少到R/2，此过程中对小球运动的正确描述是（    ）

（A）线速度大小不变，角速度增大

（B）线速度、角速度都不变

（C）线速度、角速度都增大

（D）线速度增大，角速度大小不变

【答案】

C

【解析】

本题中绳的拉力就是小球的向心力，向心力增大，小球质量不变，所以向心加速度也增大，由向心加速度公式a＝ω²r＝\(\frac{{{v^2}}}{r}\)可知，当a增大，r减小时ω必然增大，而且a增大到8倍，r减小到1/2，v也应该增大。

 

5．物体做匀速圆周运动时，以下说法中正确的是（     ）

（A）必须受到恒力的作用               （B）物体所受合力必须等于零

（C）物体所受合力大小可能变化     （D）物体所受合力大小不变，方向不断改变

【答案】

D

 

6．一个做匀速圆周运动的质点，如果它的轨道半径不变，周期增大，则它的（    ）

（A）速度增大，加速度增大            （B）速度增大，加速度减小

（C）速度减小，加速度增大            （D）速度减小，加速度减小

【答案】

D

 

7．质量为6×10² kg的汽车，以10 m/s的速度驶过半径为80 m的圆环形车道，求汽车的向心加速度和所需的向心力。

【答案】

1.25 m/s²，750 N

 

8．甲、乙两质点都做匀速圆周运动，甲的质量是乙的质量的\(\frac{1}{3}\)，甲的圆周半径是乙的\(\frac{3}{4}\)，当甲转动60圈时，乙转动45圈，则甲、乙运动周期之比为________，甲、乙两质点的向心加速度之比为______，向心力之比为_________。

【答案】

3∶4，4∶3，4∶9

 

9．从式a＝ω²r看好像a跟r成正比，从式a＝\(\frac{{{v^2}}}{r}\)看好像a跟r成反比。如果有人问你：“向心加速度的大小跟半径成正比还是成反比”，应该怎样回答？

【答案】

条件不明确，不能下结论。当ω不变时，a与r成正比，当v不变时，a与r成反比

 

10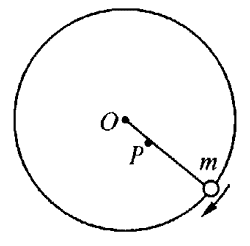．一个被细绳拉住的小球m，在光滑水平面上做匀速圆周运动，圆心为O。在运动过程中，细绳被固定在光滑平面上的一枚铁钉P挡住，如图所示。这时小球的线速度________，角速度______，加速度________，细绳的拉力_____（填变大、变小、不变）。

【答案】

不变，变大，变大，变大

 

11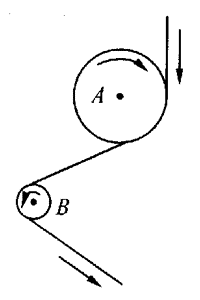．在某传动装置中有A、B两轮，它们以皮带相连，如图所示。若A、B两轮的半径之比为3∶1，则A、B两轮边缘质点的向心加速度的比多大？

【答案】

1∶3

 

12．线的一端系一个重物，手执线的另一端使重物在光滑水平桌面上做匀速圆周运动，当转速相同时，线长易断，还是线短易断？为什么？如果重物运动时系线被桌上的一个钉子挡住，随后重物以不变的速率在系线的牵引下绕钉子做圆周运动，系线碰钉子时钉子离重物越远线易断还是越近线易断？为什么？

【答案】

线长易断，因为F＝mω²r，当转速相同时，F与r成正比，线越长小球所需向心力越大，钉子离重物近，细线易断，因为速率不变时，由F＝m\(\frac{{{v^2}}}{r}\)，F与r成反比，距离越近，细线承受的向心力越大。

 

13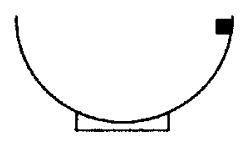．如图所示，有一个质量为m的木块，从内壁粗糙的半球形碗边下滑，在下滑过程中，如果由于摩擦作用，木块的速率恰能保持不变，下列说法中正确的是（    ）

（A）因木块的速率不变，说明它的加速度为零，合外力也为零

（B）木块下滑的过程中，所受到的合外力越来越大

（C）木块下滑的过程中，摩擦力的数值不变

（D）木块下滑的过程中，加速度数值恒定，方向不断改变，始终沿着半径指向圆心

【答案】

D

 

14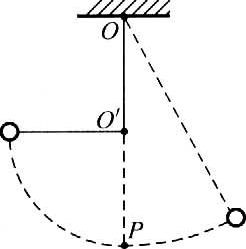．质量为 m 的小球用长为l的线悬挂在 O 点，在 O 点正下方 \(\frac{l}{2}\) 处有一光滑的钉子 d，把小球拉到与 d 在同一水平面的位置，摆线被钉子拦住，如图所示，再将小球从静止释放。当球第一次通过最低点P时（    ）

（A）小球速率突然减小

（B）小球角速度突然减小

（C）小球的向心加速度突然减小

（D）摆线上的张力突然减小

【答案】

BCD

 

15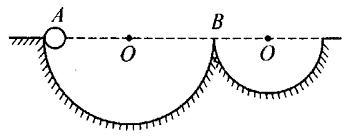．如图所示，两个半径不同而内壁光滑的半圆轨道固定在地面，一个小球先后从与球心在同一高度的A、B两点由静止开始自由下滑，通过两轨道最低点时（    ）

（A）小球对两轨道的压力相同

（B）小球对两轨道的压力不同

（C）小球的向心加速度不相等

（D）小球的向心加速度相等

【答案】

AD

 

16．一小球做半径为r的匀速圆周运动，线速度大小为v，若该小球速度矢量变化的大小也是v，所需的最短时间是____。

【答案】

πr/3v

 

17．如图所示，在光滑的水平面上钉两个钉子A和B，相距20 cm，用一根1 m长的细绳，一端系一质量为0.4 kg的小球，另一端固定在钉子A上，开始时小球与A、B两钉在同一直线上，如图所示，然后使小球以2 m/s的速率在水平面上做匀速圆周运动，如果绳所能承受的拉力为4 N，问从小球开始运动到绳被拉断经历了多长时间？

【答案】

1.2π s

 

18．一根长为L的均匀细杆可以绕通过其一端的水平轴O在竖直平面内转动，杆最初处于水平位置，杆上离轴O距离为a处放有一可视为质点的小物体，杆与其上小物体最初均处于静止状态，如图所示，若此杆突然以匀角速度ω顺时针绕O轴转动，问当ω取什么值时，小物体与杆可能相碰 ？

【答案】

ω＜\(\frac{{\sqrt {\frac{g}{2}} \arccos \frac{a}{L}}}{{\sqrt[4]{{{L^2} - {a^2}}}}}\)，ω＞\(\frac{{\sqrt {\frac{g}{2}} (\arccos \frac{a}{L} + 2\pi )}}{{\sqrt[4]{{{L^2} - {a^2}}}}}\)

 

19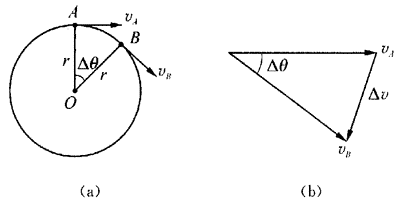．除了根据牛顿第二定律，由向心力公式推出向心加速度公式外，我们还可以直接用运动学知识推出向心加速度公式，请阅读以下推导过程，并说出其中体现了什么重要的思想。

如图（a）所示，质点沿半径为r的圆周做匀速圆周运动，在某时刻处于A点，速度是v_A，经过很短的时间Δt后，运动到B点，速度是v_B。在图（b）中，按照矢量相加的运算法则，质点从A点运动到B点时速度的变化量为Δv，A、B两点的速度和速度的变化量构成一个矢量三角形，质点在Δt时间内的平均加速度a＝\(\frac{{\Delta v}}{{\Delta t}}\)，平均加速度的方向就是矢量Δv的方向。当Δt趋近于零时，B点无限靠近A点，平均加速度的极限就是质点在A点的瞬时加速度。在图（b）中，v_A和v_B的大小相等，当Δt趋近于零时，v_A和v_B的夹角也趋近于零，这时Δv的方向就垂直于v_A，即沿着半径指向圆心，因此，质点做匀速圆周运动时，它在任一点的瞬时加速度都是沿着半径指向圆心的，我们就把匀速圆周运动的加速度叫做向心加速度，向心加速度反映了速度方向的变化快慢。那么向心加速度的大小是多少呢？推导过程如下，由加速度的定义可知，a＝\(\frac{{\Delta v}}{{\Delta t}}\)，当Δt趋近于零时，图（b）中的Δθ角也趋近于零，此时Δθ角所对的弧长和弦长Δv的差异可以忽略，即Δv＝vΔθ。因此，a＝\(\frac{{\Delta v}}{{\Delta t}}\)＝\(\frac{{v\Delta \theta }}{{\Delta t}}\)＝vω＝\(\frac{{{v^2}}}{r}\)。运用线速度与角速度的关系，还可得出a＝ω²r，这就是我们前面用实验和牛顿定律得出的向心加速度公式。

【答案】

体现极限思想。

 

20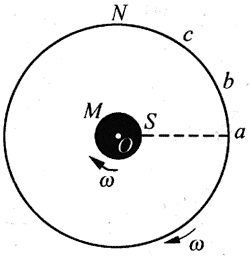．图中M，N是两个共轴圆筒的横截面，外筒半径为R，小筒半径比R小很多，可以忽略不计，筒的两端是封闭的，两筒之间抽成真空，两筒以相同的角速度ω绕其中心轴线O（图中垂直于纸面）做匀速转动。设从M筒内部可以通过窄缝S（与筒的轴线平行）不断地向外射出两种不同速率v₁和v₂的微粒，从S处射出时的初速度的方向都是沿筒的半径方向，微粒到达N后就附着在N筒上，如果R、v₁和v₂都不变，而ω取某合适的值，则以下结论正确的是（    ）

（A）有可能使微粒落在N筒上的位置都在口处一条与S缝平行的窄条上

（B）有可能使微粒落在N筒上的位置都在某一处（如b处）一条与S缝平行的窄条上

（C）有可能使微粒落在N简上的位置分别在某两处（如b处和c处）与S缝平行的窄条上

（D）只要时间足够长，N筒上将到处落有微粒

【答案】

ABC

【解析】

当v₁，v₂、ω都不变时，粒子从M筒到达N筒和筒转一周所用的时间都是确定的，设它们分别用t₁、t₂和T表示，粒子落在什么地方取决于这三个时间的关系。如果T恰好是t₁和t₂的公约数，那么两种不同速度大小的粒子都落在同一点以处；如果和的余数相等且不为零，两种不同速度大小的粒子将落在a处之外的某一b处；如果和的余数不相等，则两种不同速度大小的粒子落在两处，由于落点离以处的弧长分别为Rωt₁＝和Rωt₂＝都有确定的值，因此在圆筒内壁上不可能到处是粒子。

 

21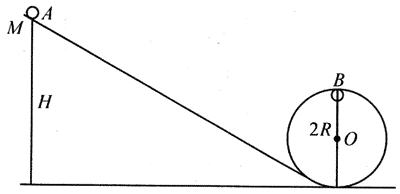．设图中圆周轨道半径R，一切摩擦不计，为保证过山车能沿圆轨道安全经过最高点B，过山车在B点的速度至少是多少？为使过山车在B点达到该速度，A点的高度应是多少 ？

【答案】

v＝\(\sqrt {Rg} \)，\(\frac{5}{2}\)R

 

22．一辆重心很低的汽车在水平面上沿半径R＝90m的弯道行驶，如果车轮与地面间最大静摩擦力等于汽车的重力，求汽车通过弯道的最大速度应多少？（g取10 m/s²）

【答案】

30 m/s

 

23．如图为验证向心力和质量、半径之间关系的一种实验仪器，球A和B可以在光滑杆OOʹ上无摩擦地滑动，两球之间用一根线连接，m_A等于km_B。两球离转轴的距离分别r_A和r_B。当仪器以转速n匀速转动时，两球最终相对光滑杆静止，求证此时r_A＝\(\frac{{{r_{\rm{B}}}}}{k}\)。

【答案】

两球绕转轴旋转时，向心力由线的拉力提供。

两球所受拉力大小相等方向相反，而且每个拉力都可用向心力公式计算。

向心力公式可得

F_A＝ω²r_Am_A＝4π²n²r_Am_A，

F_B＝ω²r_Bm_B＝4π²n²r_Bm_B，

因为一根绳两端的拉力相等，即F_A＝F_B。

证得\(\frac{{{r_{\rm{A}}}}}{{{r_{\rm{B}}}}}\)＝\(\frac{{{r_{\rm{A}}}}}{{{r_{\rm{B}}}}}\)＝\(\frac{1}{k}\)，r_A＝\(\frac{{{r_{\rm{B}}}}}{k}\)。

 

24．旋转餐厅转动一周的时间约为一小时，餐桌离转轴的距离约为20 m，请通过估算，说明就餐的顾客为什么感觉不到向心力的作用。

【答案】

估算后可知顾客受到的向心力很小，所以感觉不到。

 

25．在道路湿滑的情况下，无论行路还是驾车，都要降低速度转弯，这是什么原因？

【答案】

道路湿滑，地面摩擦所能提供的向心力很小，必须降低转弯速度，才能保证安全。

 

26．一辆质量m＝2.0×10³ kg的汽车在水平公路上行驶，经过半径r＝50 m的弯路时，如果车速v＝72 km/h，这辆汽车会不会发生侧滑？已知轮胎与路面间的最大静摩擦力F_fmax＝1.4×10⁴ N。

【答案】

所需向心力为1.6×10⁴ N，超过最大静摩擦力，汽车一定侧滑。

 

27．运用圆周运动的知识可以测定子弹的速度。图中纸质圆筒绕中心轴O以角速度ω顺时针旋转，子弹以一定速度沿与轴线平行的方向，从圆筒的一个底面的A点射入，从另一个底面的B点射出，射入点与射出点所在半径的夹角为θ，若圆筒的长度为l，求子弹的速度v。

【答案】

v＝\(\frac{{k\omega }}{{2\pi (n + 1) - \theta }}\)或\(\frac{{k\omega }}{{2\pi n + \theta }}\)，式中n为正整数。

 

28．如图中所示，为什么赛车场和铁轨的弯道处，路基都要设计成倾斜的？

【答案】

赛车速度很高，火车质量很大，转弯时都需要很大的向心力，仅仅依靠地面摩擦力作为向心力，往往还不够。把路基设计成倾斜，可以利用斜面支持力的水平分力补充向心力，以保障安全。

 

29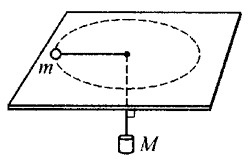．图中所示的光滑水平面中央有一圆孔，一根细线穿过圆孔，它的两端分别跟质量为m的小球和质量为M的钩码相连，如果小球在水平面上做半径为r的匀速圆周运动，钩码位置保持不变，小球做匀速圆周运动的向心力是多少？线速度是多少？在运动过程中，如果小球的线速度减小了，将会发生什么现象？

【答案】

F_向＝Mg；v＝\(\sqrt {\frac{{Mgr}}{m}} \)；

在运动过程中，如果小球线速度减小，Mg将大于小球所需要的向心力，小球运动半径减小，钩码将竖直向下运动，最后小球到达圆心。？？？？？？？（我认为实际情况非常复杂，没这么简单）

 

30．质量为6×10³ kg的汽车，以10 m/s的速度驶过半径为80 m的圆环形水平车道，则地面与轮胎间摩擦因数至少为多大，才能提供足够的向心力，保证行车安全？

【答案】

0.125

 

31．飞机进行特技飞行表演时，在竖直平面内做圆周运动，若圆周半径r＝200 m，飞行员的质量m＝75 kg，飞机经过最高点P时飞行员对座位的压力恰好为零。求此时飞机的速度大小。

【答案】

v≈45 m/s

 

32．在质量为M的小桶中盛上质量为m的水，小桶拴在长为l的绳子一端，绳的另一端用手握住，使小桶在竖直平面内做圆周运动，为使水不从小桶内流出，小桶转到最高点时的线速度至少应该多大？

【答案】

v＝\(\sqrt {gl} \)

 

33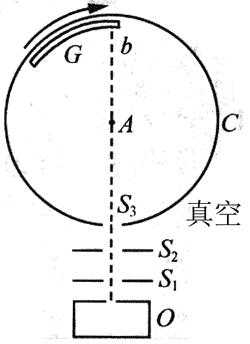．如图为蔡特曼（Zartman）用了测定分子速度大小的装置。O是一个小炉，金属银在其中熔化并蒸发，银原子由小孔逸出，穿过狭缝S₁、S₂成分子射线进入抽空区域，圆筒C可绕水平轴A以角速度ω＝100 rad/s转动。若C不转，分子束穿狭缝S₂进入圆筒，投射到弧形玻璃板G上的b₁点，并粘附在该处。当C以角速度ω转动时，将发现有分子粘附在G板上的b₂处，量得b₁和b₂间的弧长s＝1 cm，已知圆筒半径为R＝10 cm，且Ab₁＝Ab₂＝r＝9 cm。试求这些分子的速度大小。

【答案】

81 m/s

 

34．图中过山车由a点从静止出发依次通过b、c、d点，请根据该图提出有关的物理问题，看谁提的问题又多又好，看谁能回答提出的问题。

【答案】

略

 

35．阅读以下短文，并用自己的语言回答“履带式两栖装甲车是如何在水上行走的”，如你认为还没有完全讲清楚，请查找有关资料进一步说明。

履带式两栖装甲车是如何在水上行走的？

坦克装甲车号称陆军之王，图中是中国新型反恐两栖装甲战车首次下水试航。它们在攻击能力、机动能力和防护能力的结合上具有其他任何军事装备都无法比拟的独特优势，无论多么复杂的地形，都挡不住它们滚滚向前的步伐。我国和世界上许多国家都拥有以坦克装甲车为主要装备的机械化部队。其中的履带式两栖装甲车及其各种变型车，不仅能爬坡越沟，而且能涉水渡河；不仅具有良好的越野性能，而且兼备一定的浮渡能力。人们一定会问：这种由钢铁堆成的庞然大物，是如何在水上行走的呢？

船在水上行走，小船靠橹槁，靠双桨，大船靠由发动机带动的螺旋桨。那么履带式两栖装甲车靠什么呢？履带式两栖装甲车主要靠由发动机带动的履带划水。履带就好比是装甲车在陆地上行走的双脚，在水上行走的双桨。大家知道，履带在水中的某一阶段做圆周运动（其余阶段做直线运动），但就如同电风扇在空中旋转一样，一般只会在原地转动，是不能前进的，两栖装甲车的研制人员，在履带的上方以及前后两端，给它装上位置和尺寸恰当的挡泥板和挡水罩，其在水上的功能就是减小履带划水时水对上半部分履带的反作用力，使车辆得以前进（或后退）。

靠履带划水，行驶的速度是很慢的，一般一小时走7km左右。为了提高速度，研制人员除在不超重的前提下增大发动机马力之外，还想了许多辅助的办法，比如，在车体尾部加装喷水推进器或螺旋桨推进器，在甲板上安装防浪板。特别是改进车体的形状，由挡水型改为滑水型（流线型），在流体动力的作用下，随着速度的增加，车体的入水部分将逐渐被托出水面，以减少水的阻力。现在世界上先进的两栖装甲突击车，其航速已达每小时30 km以上。

【答案】

略

 

36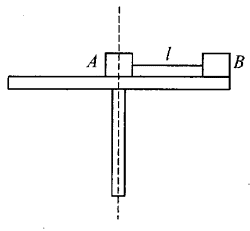．图中转台可绕其中心竖直轴转动，转台中心放一个质量为m的物体A，转台上离中心距离为l处再放一个质量同为m的物体B，两物体与水平台面的最大静摩擦力等于各自重力的k倍，现用一根不可伸长的轻质绳将它们连接在一起，当转台匀速转动时，要使物体与转台间不发生相对滑动，试分析两物体的受力情况，并回答转台的角速度是否有最大值。

【答案】

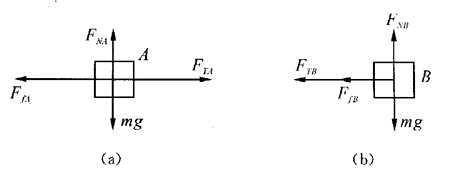
首先确定B物体为研究对象，当转台转动时，B物体随转台做匀速圆周运动，开始仅靠指向圆心的静摩擦力即可维持圆周运动，当角速度增大时，还需要绳的拉力，在竖直方向上，B物体受到的重力mg和转台对B物体的支持力F_NB相平衡，其受力示意图如图（b）所示，而A物体受力示意图如图（a）所示，A作为位于轴心的质点，不做圆周运动，沿半径方向的静摩擦力和绳的拉力平衡，说明绳的拉力也有最大值，就是A物体受到的最大静摩擦力。于是，使B物体做匀速圆周运动的向心力由B物体受到的静摩擦力和绳对B物体的拉力提供，如果转速越大，所需静摩擦力也越大，直至达到最大静摩擦力。也就是说转台的角速度有最大值，超过最大值，两物体都要被甩出平台。

 

37．在人们常见到的以下现象中，属于离心现象的是（    ）

（A）舞蹈演员在表演旋转动作时，裙子会张开

（B）在雨中若把伞柄转动一下，伞面上的雨水将会很快地沿伞面运动，到达边缘后雨水将沿切线方向飞出

（C）满载黄砂或石子的卡车，在急转弯时，部分黄砂或石子会被甩出

（D）守门员把足球踢出后，球在空中沿着弧线运动

【答案】

ABC

 

38．一圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动。在圆盘上放置一木块，当圆盘匀速转动时，木块随圆盘一起运动，那么此时（    ）

（A）木块受到圆盘对它的摩擦力，摩擦力方向背离圆盘中心

（B）木块受到圆盘对它的摩擦力，摩擦力方向指向圆盘中心

（C）因为摩擦力总是阻碍物体运动，所以木块所受圆盘对它的摩擦力的方向与木块的运动方向相反

（D）因为圆盘与木块是相对静止的，所以圆盘与木块之间无摩擦力

【答案】

B

 

39．物体放置在旋转的水平圆台上，当圆台的转速增大时，该物体仍与圆台保持相对静止，则（    ）

（A）物体所受的静摩擦力增大               （B）物体对圆台的弹力增大

（C）圆台对物体的最大静摩擦力增大     （D）物体所受的合力增大

【答案】

AD

 

40．有一种大型游戏器械，它是一个圆筒形的大容器，游客进入容器后靠筒壁坐着，如图所示。当圆筒开始转动，转速逐渐增大时，游客会感到自己被紧紧地压在筒壁上不能动弹。当转速增大到一定程度时，突然地板与坐椅一起向下坍落，游客们大吃一惊，但他们都惊奇地发现自己是安全的。请回答：这时人们做圆周运动所需的向心力是由什么力提供的？人们自身所受重力又是被什么力所平衡？

【答案】

做圆周运动所需的力是圆筒壁对游客的压力，沿半径方向指向圆筒轴线。游客自身重力是被圆筒对游客的摩擦力平衡，该摩擦力的方向竖直向上，只要圆筒转速足够高，圆筒对游客提供的向心力即正压力就足够大，摩擦力也足以平衡游客的重力。

 

41．水平转台上放有两个物体A和B，它们随转台一起匀速转动无相对滑动，如果它们质量之比m_A∶m_B＝2∶1，离转轴距离之比r_A∶r_B＝3∶2，则它们所受静摩擦力之比F_fA：F_fB＝______，线速度之比v_A：v_B＝____。

【答案】

3∶1，3∶2

 

42．在水平转盘上放两块相同木块A和B，木块A离转轴较远，木块B离转轴较近，当转盘越转越快时，木块B不容易滑动，木块A容易飞出，造成这种现象的原因是（    ）

（A）因为木块A受的向心力比较大，向心力帮助它飞出

（B）因为ω_A＞ω_B，所以木块A容易打滑而飞出

（C）因为最大静摩擦力相同，而木块A所需向心力比木块B所需向心力大，所以木块A容易打滑而飞出

（D）由于木块A、B所受静摩擦力不同，木块A所受静摩擦力大，应当不容易飞出，故本题所述现象不可能发生

【答案】

 C

 

43．在旋转的圆筒内壁上紧贴一个物体，物体随圆筒一起运动，当圆筒的转速增大后，该物体仍处在原来位置，则（    ）

（A）物体受到的静摩擦力增大               （B）物体对圆筒的弹力增大

（C）圆筒对物体的最大静摩擦力增大     （D）物体受到的合力增大

【答案】

BD

 

44．如图所示是用来研究圆周运动的仪器，球A、B可以在光滑杆上无摩擦地滑动，两球之间用一细轻线连接，若m_A＝2m_B，当仪器以角速度ω匀速转动，并达到稳定时，则（    ）

（A）两球向心力大小相等

（B）r_A＝\(\frac{1}{2}\)r_B

（C）两球的向心加速度大小相等

（D）当ω增大时，B球向外运动

【答案】

AB

 

45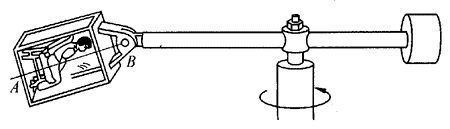．飞机俯冲拉起时，飞行员处于超重状态，即飞行员对座位的压力大于他所受的重力，这种现象也叫过荷，这时会造成飞行员大脑贫血，四肢沉重，过荷过大时，飞行员还会暂时失明，甚至晕厥。飞行员可以通过加强训练来提高自己的抗荷能力，图中所示是训练飞行员用的一种离心试验器。当试验器转动时，被训练人员根据测试要求，在试验舱内可取坐、卧等不同姿势，以测试离心作用对飞行员产生的影响，离心试验器转动时，被测验者做匀速圆周运动。现观察到图中的直线AB（即垂直于座位的直线）与水平杆成30°角。被测验者对座位的压力比他所受重力大还是小？为什么？

【答案】

题中座位的压力就是坐垫对飞行员的压力，其方向与水平方向成30°，由矢量图可知F＝\(\frac{G}{{\sin 30^\circ }}\)＝2G

 

46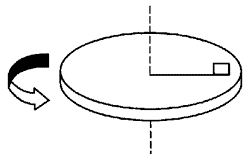．如图所示，质量为0.1 kg的木块放在半径为0.5 m的水平转盘上，已知木块与转盘间的最大静摩擦力为0.4 N，当转盘以60 r/min的转速匀速转动时，要使木块随盘一起转动而无相对滑动，木块距轴的最大水平距离为多少？木块的向心加速度多大？

【答案】

0.1 m/s，4 m/s²

 

47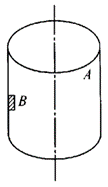．半径为R的圆筒A绕其竖直的中心轴匀速转动，其内壁上有一个质量为m的物体B（如图所示），B一边随圆筒A转动，一边以竖直向下的加速度a下滑，如A、B间摩擦系数为μ，则圆筒A的转动角速度是多少？

【答案】

ω＝\(\sqrt {\frac{{g - a}}{{\mu R}}} \)

【解析】

在竖直方向，有mg－μF_N＝ma；在半径方向，有F_N＝mω²R，得ω＝\(\sqrt {\frac{{g - a}}{{\mu R}}} \)

 

48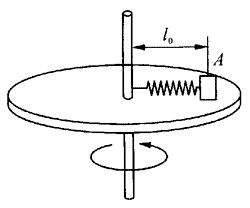．在水平放置的可旋转的圆台上面放一根劲度系数为k，原长为l₀，质量可忽略不计的轻弹簧。弹簧的一端固定在轴上，另一端连接一个质量为m的物体A，如图所示。如果物体能够随圆盘一起以角速度ω转动，并且可以沿径向自由滑动，求弹簧的伸长。

【答案】

x＝\(\frac{{m{\omega ^2}{l_0}}}{{k - m{\omega ^2}}}\)

 

49．有一水平圆盘绕其中心轴转动，转速为\(\frac{{60}}{\pi }\)r/min。现把质量为1 kg物体置于盘上，物体和盘的最大静摩擦力为2.4 N，为保持物体和盘相对静止，则：

（1）物体离转轴的最大距离L是多少？

（2）这时摩擦力的方向指向何处？

（3）若物体离转轴0.2 m，物体所受合力为多大？

【答案】

（1）0.6 m

（2）指向圆盘中心

（3）0.8 N

 

50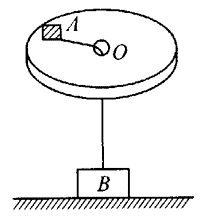．在光滑水平台面上开着一小孔O，一根轻绳穿过小孔，一端拴一质量为0.1 kg的物体A，另一端连接质量为1kg的物体B，如图所示，已知O与A物间的距离为25 cm，开始时B物体放在水平地面上，那么，

（1）当A物体以角速度ω＝4 rad/s旋转时，B物体对地面的压力多大？

（2）要使B物体离开地面，则A物体转动的角速度至少为多大？

【答案】

（1）9.4 N

（2）19.8 rad/s