1．铁道上的列车车厢经常需要分类编组，图（a）所示的就是常用的“驼峰”编组站，它是一种为列车提供分解车体进行编排组合各种车厢的设施。它因从侧面看酷似骆驼的背部而得名。图（b）、（c）是它的俯视图和侧视图，列车大约以1.2 m/s的速度倒着将车厢推至峰顶，然后脱开车钩，让车厢滑入应进入的车道，实行编组。为了防止进入编组道的车速过大，滑行途中还装有减速器。

如果车厢未经减速器，也不计阻力，它滑到底部速度是8 m/s，那么驼峰的高度为多大？

【答案】

h＝3.1 m

 

2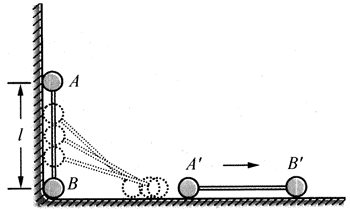．如图所示，质量为m的A球与质量为2m的B球由轻杆相连，两球心间距离为l，放置在成直角的光滑槽内。开始时轻杆成竖直状态，两球均处于静止状态。放开后，A球沿竖直槽壁向下滑动，B球沿水平槽壁向右滑动，最终两球一起在水平槽中滑动，求两球最终速度。

【答案】

v＝\(\sqrt {\frac{2}{3}gl} \)

 

3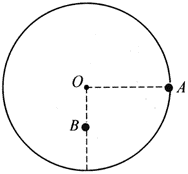．如图所示，半径为r，质量不计的圆盘盘面与地面相垂直，圆心处有一个垂直盘面的光滑水平固定轴O，在盘的最右边缘处固定一个质量为m的小球A，在O点的正下方离O点\(\frac{r}{2}\)处固定一个质量也为m的小球B，放开盘让其自由转动，问：

（1）A球转到最低点时线速度为多大？

（2）在转动过程中半径OA向左偏离竖直方向的最大角度是多少？

【答案】

（1）v_A＝\(\sqrt {\frac{4}{5}gr} \)

（2）θ＝37°

 

4．如图所示，一个质量为m的足球被以v₀速度由地面踢起。当它到达离地面高为h的B点时，如取B点为零重力势能参考平面，下列说法中正确的是（    ）

（A）在B点处重力势能为mgh

（B）在B点处的机械能为\(\frac{1}{2}\)mv₀²－mgh

（C）在B点处的机械能为\(\frac{1}{2}\)mv₀²＋mgh

（D）在B点处的动能为\(\frac{1}{2}\)mv₀²－mgh

【答案】

BD

 

6．下列两种情况，系统的机械能是否守恒？为什么？

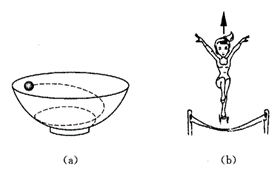
（A）一颗弹丸在光滑的碗内做复杂的曲线运动[图（a）]；

（B）运动员在蹦床上越跳越高[图（b）]。

【答案】

（A）守恒，只有重为做功

（B）不守恒，人在做功机械能增大

 

9．在下列各种情况下，判断机械能是否守恒。（守恒用“√”，不守恒用“×”表示）

（1）如图（a），小车表面粗糙、载着重物从光滑斜面上自由下滑过程中重物的机械能______。

（2）弹簧一湍固定，另一端系住小车，如图（b）所示，内表面粗糙的小车中载有一个重物，水平地面光滑，当小车左右振动时，若物体在车中滑动，这个系统的机械能______；若物体与车始终相对静止，这个系统机械能____。

（3）如图（c）所示天平，两盘中都载有重物，正在轻轻摆动（阻力不计）。这个系统的机械能________，每个重物的机械能________。

【答案】

（1）√（2）×，√（3）√，×

 

11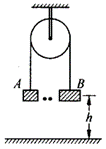．如图所示，质量为m的A物体与质量为2m的B物体，通过跨过定滑轮的细绳联系在一起。开始时它们在同一高度h处，放手后开始运动，当B抵达地面时的速度为多大？

【答案】

\(\sqrt {\frac{{2gh}}{3}} \)

 

12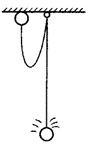．如图所示，长为1.8 m的轻绳，上端悬挂在离地面3.6 m高的天花板上，下端系一个质量为2 kg的小球。现将球拉到天花板，放手后球自由下落，在轻绳绷紧时，绳断球落地，从放手到球落地整个时间为1.2 s。 若小球与绳作用时间及绳的伸长均可忽略不计，则小球克服绳的拉力所损失的机械能为多大？

【答案】

取g＝10 m/s²，下降到断裂处时间为0.6 s，断后下落同样高也是0.6 s，所以断后速度为零，则ΔE_k＝\(\frac{1}{2}\)mv_t²＝36 J

 

14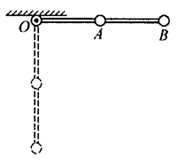．一根长为L的轻质直杆，可绕光滑转轴O自由转动，在其中点和另一端分别固定质量都为m的小球A、B，将杆由水平位置从静止释放，当杆到达竖直位置时，则B球的线速度的大小为多少？

【答案】

\(\sqrt {\frac{{12gh}}{5}} \)

 

15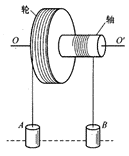．如图所示，一个轻质轮轴，轮的半径为R，轴的半径为r（R＝3r）。在轮周绕有轻绳，绳端悬挂一质量为M的重物A。在轴上也绕有轻绳，绳端悬挂一质量为m的重物B（M＝2m）。开始时AB在同一高度。自静止起放手后，A下降B上升。求A下降h高度时速度的大小。（摩擦及其他阻力不计）

【答案】

v_A＝\(\sqrt {\frac{{30gh}}{{19}}} \)

 

16．下列生活中常见的事例，可以近似应用机械能守恒定律的是（    ）

（A）游乐场中摩天轮的转动

（B）高山滑雪者在空中飞跃

（C）打桩机重锤从提升到释放下落的全过程

（D）汽车关闭油门从桥上快速下行

【答案】

BD?

 

18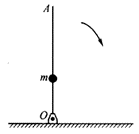．如图所示，通过铰链固定在地面转动轴O上的一根轻质直竿长为L，在离竿O点一定距离处固定一个重物m，放手后让竿倒下。设竿到达水平位置时竿端A的速度为v，则m离O的高度为______。

【答案】

2gL²/v²

 

18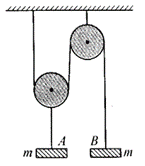．一个由动滑轮和定滑轮组成的滑轮组（如图），在它们的下方分别悬挂质量均为m的重物（滑轮的质量不计，一切阻力不计）。开始时两物体处于静止状态，释放后发生运动，当A的位移为h时，问两物体的速度各为多大？

【答案】

v_A＝\(\sqrt {\frac{{2gh}}{5}} \)，v_B＝2\(\sqrt {\frac{{2gh}}{5}} \)

 

19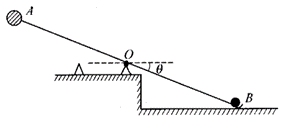．如图是一种抛物器，轻质杠杆左端A是一个质量为M的重球，OA长为l，杠杆的右端是一个被抛的物体B，质量为m，OB也为l。此时杠杆与水平面的夹角为θ。释放后杠杆逆时针转动，物体最后被竖直向上抛出，若M＝10 kg，m＝0.5 kg，l＝1 m，θ＝30°，求物体上升离抛出点的最大高度。

【答案】

H＝0.45 m

 

20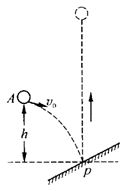．如图所示，将一个质量为m的弹性球，以某一速度投向斜面，恰好能竖直向上弹起。若投出点离碰击点p的竖直高度为h，今要使弹起的高度为3h，则抛球速度至少应多大？（碰击损失不计）

【答案】

2\(\sqrt {gh} \)

 

21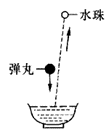．试说明图中一颗小弹丸从离水面不高处落入水中为什么溅起来的几个小水珠可以跳得很高？（不计能量损失）

【答案】

不计能量损失MgH应与mgh相当，因M≫m，所以h≫H，故跳得很高

 

23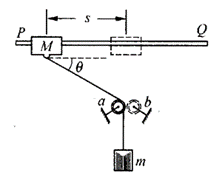．质量为M的滑块套在光滑的水平长杆PQ上，它的下面所系的细线跨过定滑轮以与质量为m的重物相连。M与滑轮间水平距离为s，开始时处于静止状态，绳与水平面夹角为θ，放手后在m的带动下M向右运动，当M运动至滑轮正上方时，m与M的速度各为多大？如果与滑轮a相对称还有滑轮b，这时你将看到什么现象？

【答案】

m下降高度h＝\(\frac{s}{{\cos \theta }}\)－stanθ，m至最低点时速度为零，则mgh＝\(\frac{1}{2}\)Mv²，v＝\(\sqrt {\frac{{2m(1 - \sin \theta )gs}}{{2M\cos \theta }}} \)，如果存在滑轮b，则M做往复运动，m上下运动

 

26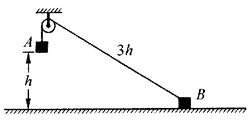．如图所示，一个定滑轮离地面适当高度，跨过它的细绳的一端连接一个质量为m的重物A（它挂在轮边，离地面高度为h），绳的另一端系住一个质量为2m的物体B。B物体可以沿光滑水平面运动，此时绳的长度为3h。放手后A下落时牵动B，求A落地时的速度。

 

【答案】

v_A＝\(\sqrt {\frac{{6gh}}{{11}}} \)

 

27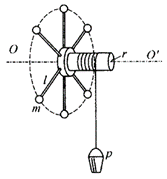．如图所示，在半径为r的轴上悬挂一个质量为M的水桶p，轴上分布着6根手柄，柄端有6个质量为m的金属球。球离轴心的距离为l。轮轴、绳及手柄的质量以及摩擦均不计，放手后在桶的重力作用下整个装置发生转动，求转动n周后水桶的速度。

【答案】

v＝\(\sqrt {\frac{{4Mg\pi nr}}{{M + \frac{{6m{l^2}}}{{{r^2}}}}}} \)

 

28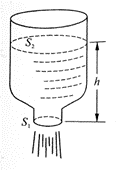．如图所示，一个盛水容器两端开口，小口的横截面积为S₁，大口的横截面积为S₂，内盛的水在不断地流出，此时的高度差为h，求此时流出小口水流的速度。（提示：上部和下部流量Q＝Sv是相等的）

【答案】

v₁＝\(\sqrt {\frac{{2ghS_2^2}}{{S_2^2 - S_1^2}}} \)