1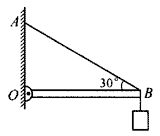．如图所示，长度为l＝1 m的杆OB可绕通过O点垂直于纸面的轴转动，绳AB的拉力为20 N，杆OB刚好水平，AB与OB的夹角为30°。求拉力的力矩。

【答案】

10N·m

 

2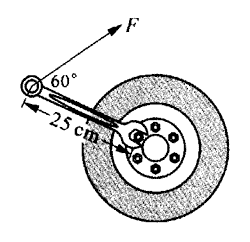．用一把柄的长度为25 cm的扳手拧紧一只汽车轮胎上的螺帽，如图所示。如果你在扳手的一端沿与扳手柄成60°角的方向上用200 N的力拉扳手，则所施的力矩是多少？

【答案】

43.3 N·m

 

3．图中各物体都受到几个力的作用，并且可以分别绕通过O点且垂直于纸面的轴转动，画出图中各个力以O点为转动轴的力臂；哪些力矩是引起顺时针方向转动的力矩？哪些是引起逆时针方向转动的力矩？哪些力对O点的力矩为零？

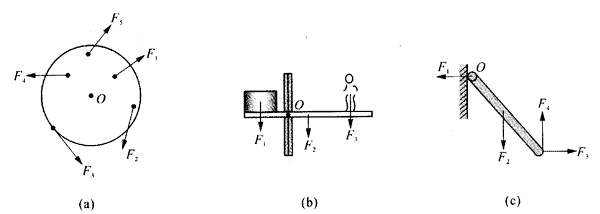
【答案】

（a）F₁的力矩为零，F₃、F₄的力矩引起物体沿逆时针方向转动，F₂、F₅的力矩引起物体沿顺时针方向转动。

（b）F₁的力矩引起物体沿逆时针方向转动，F₂、F₃的力矩引起物体沿顺时针方向转动。

（c）F₁的力矩为零，F₃、F₄的力矩引起物体沿逆时针方向转动，F₂的力矩引起物体沿顺时针方向转动。

 

4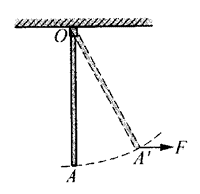．OA是一根长为l，质量为m的均匀铁棒，可绕O点的轴自由转动，问：当恒定外力F将它拉到如图所示位置的过程中，该棒所受的重力是否改变？重力对O点的力臂和力矩是否改变？怎样改变？F对O点的力臂和力矩是否改变？怎样改变？

【答案】

重力不变，重力对O点的力臂（\(\frac{l}{2}\)sinθ和力矩（\(\frac{l}{2}\)mgsinθ）随θ的增加而增加；F对O点的力臂（lcosθ）和力矩（lmgcosθ）随θ的增加而减小。

此题不合适，最好改成匀速转动，更符合本章的知识点。

 

5．如图所示，直杆OA可绕通过O点，且垂直于纸面的轴转动，杆的A端分别受到F₁、F₂、F₃、F₄的作用。已知力的作用线都在纸面内，且这四个力的矢量末端均落在一条与OA平行的虚线上，设它们对O轴的力矩分别为M₁、M₂、M₃、M₄，则这四个力矩大小的关系是（    ）

（A）M₁＞M₂＞M₃＞M₄

（B）M₁＝M₂＝M₃＝M₄

（C）M₁＜M₂＜M₃＜M₄

（D）以上说法都不对

【答案】

B

 

6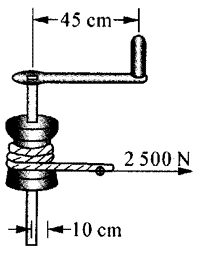．在如图所示的绞盘的把手上，应至少施以多大的力，才能使紧绕在滚筒上的绳子产生2500 N的拉力？滚筒和把手的尺寸如图中所示。

【答案】

555.6 N

 

7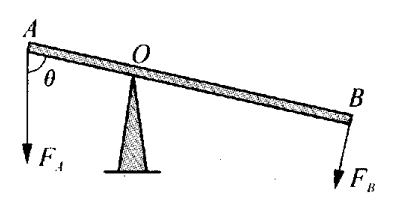．如图所示，杠杆AB可绕通过O点，且垂直于纸面的轴转动。它受到两个力作用，力F_A的大小为80 N，其作用线与AO的夹角为θ＝60°；F_B的大小为30 N，方向与OB垂直。AO＝0.8 m，OB＝2.2 m。求F_A和F_B对于转轴O的力矩。

【答案】

55.4 N·m；66 N·m

 

8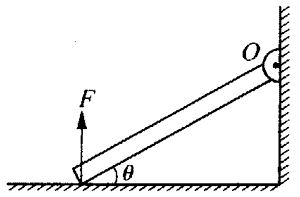．一根长为L、重为G的均匀杆，一端搁在光滑水平地面上，另一端为转轴，如图所示。杆与水平地面的夹角为θ，则杆所受重力对转轴的力矩为_______。如果地面对杆的支持力为F，则支持力F对转轴的力矩为__________。

【答案】

\[\frac{L}{2}\]Gcosθ；LFcosθ

 

9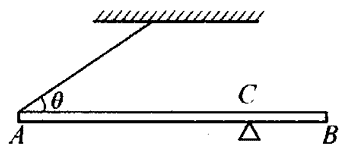．如图所示，AB是一根质量为m、长度为L的均匀金属杆，静止在水平位置，其A端用细绳悬挂，细绳与水平面的夹角为θ；转轴在C点，BC长L/4，问：这根金属杆的AC段和CB段的重力对C点的力矩分别是多少？如果细绳的拉力为T，那么该拉力对C点的力矩又是多少？

【答案】

\(\frac{9}{32}\)mgL；\(\frac{1}{32}\)mgL；\(\frac{3}{4}\)TLsinθ

 

10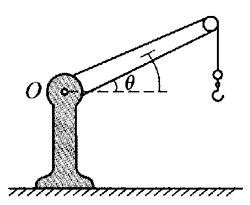．如图所示，小型臂式起重设备的吊杆质量为150 kg，其重心与转轴O的距离是吊杆长度的。当吊杆与水平方向的夹角为θ＝30°时，最大安全负载为3000 N。如果这一最大负载是由O处的转轴所能承受的最大力矩所确定的，那么当θ＝45°和60°时，这台起重机的最大安全负载分别是多少？

【答案】

3807 N；5626 N

 

11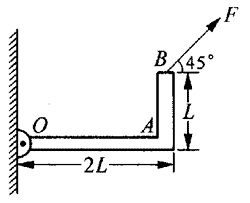．如图所示，重为G的L型匀质杆的一端O通过铰链与墙体连接，一个力F作用在B端，当F与水平面成α＝45°角时，杆的OA边恰好静止在水平方向。已知OA长为2L，AB长为L。试分别用先求力臂的方法和力的分解方法计算力对转轴O的力矩M。

【答案】

\(\frac{{\sqrt 2 }}{2}\)FL

 

12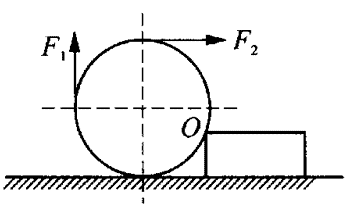．将一个横卧的油桶推上高为h的台阶。油桶的半径为R（R＞h），竖直向上的推力F₁作用在桶的最左边的一点，同时F₂作用在桶的最高点，如图所示。则推力F₁和F₂对转动轴O的力矩各是多少？

【答案】

F₁（R＋\(\sqrt {2Rh - {h^2}} \)）；F₂（2R－h）

 

13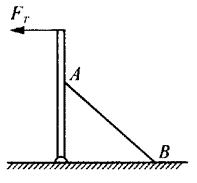．如图所示，一根长4 m的木杆，假定下端用铰链固定在地面上，杆的顶端有根水平电线向左拉，拉力F_T恒为500 N。杆的右边用一根长度为4 m的钢绳将杆垂直固定在地面上。

（1）如果钢绳上端A离地面的高度为3.5 m，此时钢绳受到的拉力是多少？

（2）为了使钢绳受到的拉力最小，其上端A离地面的高度应是多少？此时钢绳受到的拉力又是多少？

【答案】

（1）1180.3 N；

（2）钢绳应固定在杆上离地面高度为2.83 m处，此时钢绳受到的拉力最小，为1000 N。

 

14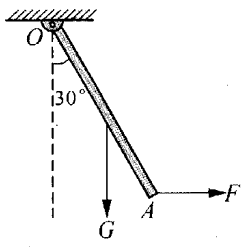．如图所示，一根均匀直杆OA可绕过O点且垂直于纸面的轴转动。为了测量杆的质量，用一个F＝12 N的水平力在A端将它拉到与竖直方向成30°角的位置并处于静止状态，杆的质量是多少？

【答案】

4.24 kg

 

15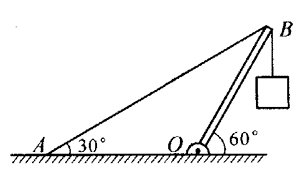．一架简单的起重机结构示意图如图所示。设均匀杆OB长为L，重为G₁，B端所挂物件的重力为G₂。杆可绕过O点且垂直于纸面的轴自由转动。杆的B端用轻质钢绳紧拉，系于地面上的A点。杆与地面成60°角，钢绳与地面成30°角。此时钢绳AB的拉力对O点的力臂为_______；悬挂物体轻质钢绳的拉力对O点的力矩为____，钢绳AB的拉力为_______。

【答案】

\(\frac{L}{2}\)；\(\frac{L}{2}\)G₂；\(\frac{{{G_1}}}{2}\)＋G₂

 

16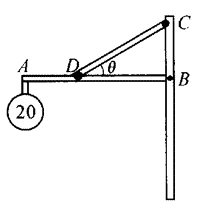．道路上有时使用的交通指示牌及其支架如图所示。若指示牌的质量为5 kg，它悬挂在长度为3 m的水平杆AB的一端，杆CD的长度为2 m，θ＝30°，这些杆的质量都不计，求CD杆中的拉力。

【答案】

169.7 N

 

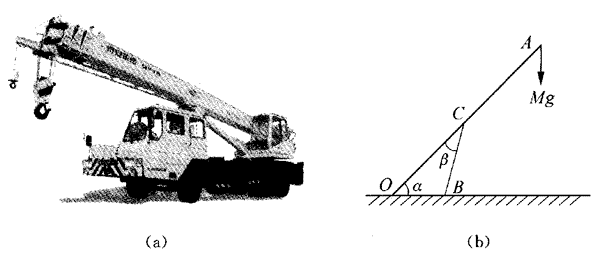
17．从图（a）起重吊车工作时的情景可抽象出一个如图（b）所示的关于力矩平衡的物理问题。质量为m＝500 kg，长度OA＝6 m的均质吊杆OA可绕通过O点且垂直于纸面的轴转动，吊杆与地面的夹角为α＝45°。A处吊挂物件的质量为M＝2000 kg。撑杆BC此时与吊杆间的夹角为β＝30°，OC＝2.5 m。求撑杆的支撑力F_T。

【答案】

6.48×10⁴ N（好像答案有误7.64×10⁴N）

 

18．如图所示，已知O为杆的中点，G＝200 N，杆的质量忽略不计。分别沿DA（水平向左）、DB（与杆垂直）、DC（竖直向上）三个不同方向用力拉住杆，使其静止，问：此时的拉力各是多少？哪一种情况最省力？为什么？

【答案】

173.2 N；86.6 N；100 N

 

19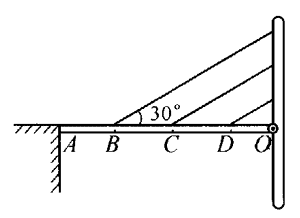．单臂斜拉桥示意图如图所示。均匀桥板重为G，可绕通过O点且垂直于纸面的轴转动，三根平行钢索与桥面成30°角，间距AB＝BC＝CD＝DO。如果每根钢索所受拉力大小相等，求拉力的大小。

【答案】

\(\frac{2}{3}\)G

 

20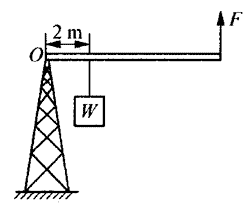．如图所示，均质杆每米重30 N，现有一重量为W＝300 N的物件挂在离转轴O的距离为2 m处，问：选用多长的杆才能使需要在另一端施加的平衡力F最小？此最小值为多少？

【答案】

2\(\sqrt {10} \) m；60\(\sqrt {10} \) N

 

21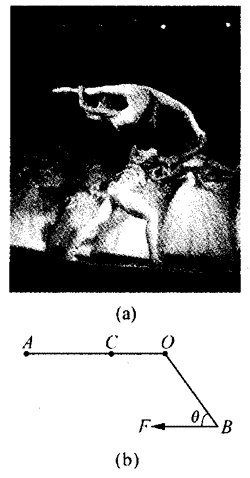．图（a）是杂技芭蕾天鹅舞中的一个动作，为了估算扮演王子的男演员右手需用拉力的大小，如图（b）所示，可将被托举的白天鹅女演员简单地抽象为一个可绕通过O点且垂直于纸面的轴转动的物体AOB，其中OB与水平方向之间的夹角为θ＝45°。设AO段的质量为m₁＝36 kg，其重心C与O点的距离为CO＝0.4 m；女演员的腿部长OB＝0.7 m，质量为m₂＝8 kg，且均匀分布，试计算水平拉力F的大小。

【答案】

229.7 N

 

22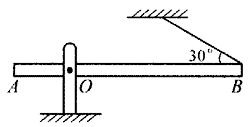．如图所示，均匀木板AB长12 m，重200 N。在距A端3 m处有一固定转动轴O。B端用绳拴住，绳与AB的夹角为30°，板AB呈水平位置。已知绳能承受的最大拉力为200 N。试确定重600 N的人在该板上行走的安全范围。

【答案】

离A端2～3.5 m

 

23．如图所示，力矩盘的重心在转轴O处，半径OA恰水平，OB⊥OA。在A、B处各挂一个相同的砝码，则力矩盘转过的角度为____时平衡。若A处挂两个相同的砝码，B处挂一个相同的砝码，则力矩盘转过的角度为____时平衡。

【答案】

45°；63.4°

 

24．一根木料长3 m，提起它的右端要用600 N的力；提起它的左端要用800 N的力。问：这根木料有多重？这根木料的重心在何处？

【答案】

重1400 N，重心离左端的距离为1.29 m

 

25．如图（a）所示，长度为L、重为G的均匀横杆，A端通过铰链固定在墙面上，另一端用钢丝绳拉成水平状态，钢绳与横杆的夹角为θ。从开始时刻起，一个质量为m，可视为质点的物体沿杆以速度v从A端匀速滑向B端。问：在小物体滑动过程中钢丝绳的拉力F_T随时间有怎样的变化关系？在图（b）上作出F_T-t图。

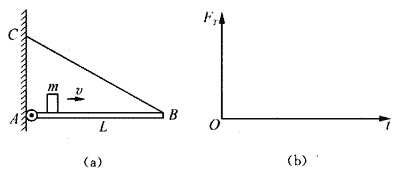
【答案】

F_T＝a＋bt，其中a＝\(\frac{G}{{2\sin \theta }}\)；b＝\(\frac{{mgv}}{{L\sin \theta }}\)

 

26．STS——关于人体某些部位的力矩平衡问题 

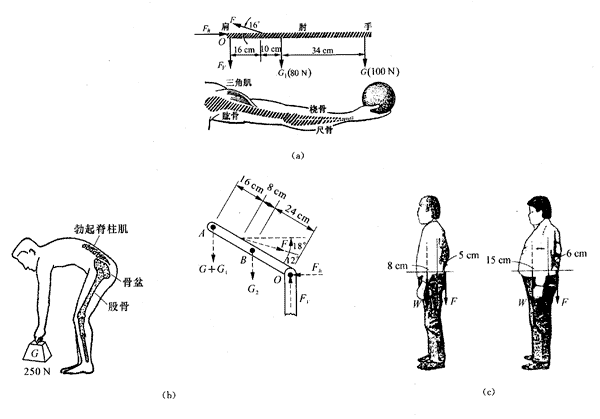
（1）如图（a）所示。手臂水平伸直，手中握有一个重100 N的重物，此时手臂主要由三角肌支承，根据图中所示尺寸计算三角肌中的总张力F。（受力图中，G₁代表手臂自身重量，它作用于手臂的重心处；F_h，F_V代表肩部的作用力）

（2）图（b）中画出了一个人正在弯腰提取G＝250 N重物的情景，在受力图上，A点处附加的G₁＝20N代表手和臂部分所受的重力；B点处的G₂＝200 N代表身体躯干部分所受的重力，它作用于躯干的重心处，试根据这一简化模型示意图，计算提起重物时勃起脊柱肌中的张力F。（受力图中F_h，F_V表示骨盆对脊柱底部的作用力。这个问题使人联想起为什么医生建议应保持脊柱竖直，尽量用腿部肌肉的力量提起重物）

（3）图（c）中画出了一位体重640 N、体态匀称的人体及一位体重 、过度肥胖的人体示意图，图中还给出了人体臀部以上部分的受力情况。W是臀部以上部分所受的重力，假定它等于总体重的，其作用点在人体这部分的重心处。该重心对于这两种类型的人体来说，分别在第五脊椎前大约8 cm和15 cm处。为了使身体不因臀部以上所受重力W的作用而弯曲，人体的背部肌肉需产生拉力F，该拉力的作用点大约分别在第五脊椎后的5 cm和6 cm处。试计算拉力F。

【答案】

（1）1.8×10³ N

（2）2.31×10³ N

（3）682.7 N（对于体格均匀的人），1500 N（对于过度肥胖的人）

 

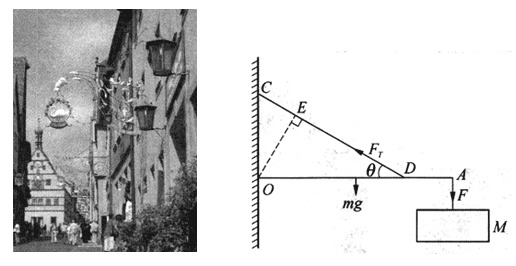
27．如图所示，商店的招牌可以做得非常漂亮。

现在来考察一个物理问题，如图所示，一块质量M为6 kg的招牌悬挂在一根质量m为1 kg、长度L为2 m的均质横杆OA上的A端处，横杆可绕通过O点且垂直于纸面的固定轴自由转动。一根细铜丝CD拉住这根横杆，使它保持在水平位置，OD的长度l为1.5 m，细钢丝与横杆的夹角θ为30°。求钢丝对横杆的拉力F_T。

【答案】

170 N

 

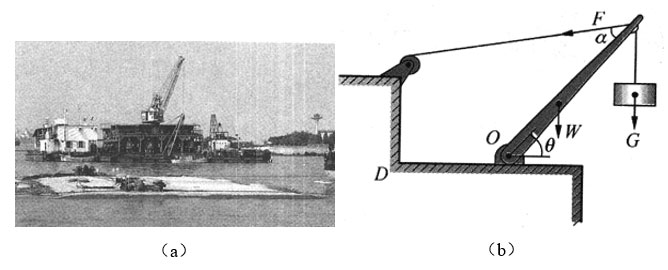
28．图（a）是上海市外环线沉管隧道施工时的现场，图（b）是一台河边码头用的起重机示意图。设起重机吊杆长l＝7.5 m，重W＝2.5 kN，其重心离底端O点距离l₀＝3m处。通过拉索可改变吊杆仰角θ。设θ＝45°，拉索的额定拉力F＝20 kN。问：当拉索与吊杆的夹角α＝30°时，这台起重机能吊起货物的最大重力G是多少？

【答案】

1.3×10⁴N

 

29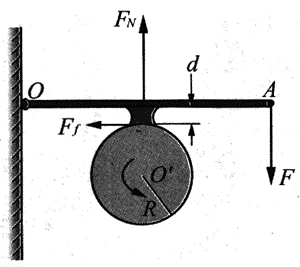．汽车的发动机能产生多大转动力矩，是一辆汽车的重要性能指标之一。

为了测量发动机在特定转速下所产生的力矩，可采用如图所示的“测力（矩）计”装置。长度为L的横杆OA可绕通过O点且垂直干纸面的轴自由转动。在A点施一竖直向下的力F，使横杆中点处的摩擦块紧紧压住安装在发动机上的正在转动的飞轮边缘，调节力F的大小，使飞轮达到某一确定的转速。此时保持横杆水平，设横杆长L＝1.2 m；摩擦块厚d＝6 cm；飞轮的半径R＝20 cm；F＝625 N；飞轮对摩擦块的压力F_N＝1290 N，忽略横杆的质量。求发动机在此转速时所产生的力矩。

【答案】

M＝80 N·m