1．篮球运动员通常伸出双手迎接传来的篮球。接球时，两手随球迅速收缩至胸前。这样做可以（    ）

A．减小球对手的冲量                  B．减小球对手的冲击力

C．减小球的动量变化量              D．减小球的动能变化量

【答案】

B

【解析】

先伸出两臂迎接，手接触到球后，两臂随球收缩至胸前，可以增加球与手接触的时间，取球的初速度方向为正方向，根据动量定理 − Ft = 0 − mv，得 F = \(\frac{{mv}}{t}\)；当时间增大时，作用力就减小，而冲量和动量、动能的变化量都不变，所以 B 正确。

 

2．一个质量是 0.05 kg 的网球，以 20 m/s 的水平速度飞向球拍，被球拍打击后，反向水平飞回，飞回的速度大小也是 20 m/s。设网球被打击前的动量为 p，被打击后的动量为 pʹ，取打击后飞回的方向为正方向，关于网球动量变化的下列计算式，正确的是（    ）

A．pʹ − p = 1 kg·m/s −（− 1 kg·m/s） = 2 kg·m/s

B．p − pʹ = − 1 kg·m/s − 1 kg·m/s = − 2 kg·m/s

C．pʹ − p = − 1 kg·m/s − 1 kg·m/s = − 2 kg·m/s

D．p − pʹ = 1 kg·m/s − 1 kg·m/s = 0

【答案】

A

【解析】

网球飞回的方向为正方向，则网球的初速度 v₀ = －20 m/s，反弹后速度：v_t = 20 m/s；网球的动量变化 Δp = pʹ − p = mv_t − mv₀ = [0.05×20 − 0.05×（− 20）] kg·m/s = 2 kg·m/s，故 A 正确。

 

3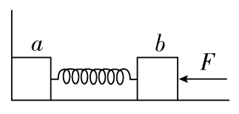．木块 a 和 b 用一根轻弹簧连起来，放在光滑水平面上，a 紧靠在墙壁上。在 b 上施加向左的水平力使弹簧压缩，如图所示。当撤去外力后，下列说法中正确的是（    ）

A．a 未离开墙壁前，a 和 b 系统的动量守恒

B．a 未离开墙壁前，a 和 b 系统的动量不守恒

C．a 离开墙后，a 和 b 系统的动量守恒

D．a 离开墙后，a 和 b 系统的动量不守恒

【答案】

BC

【解析】

a 未离开墙壁前，受到墙的作用力，系统所受外力不为零，所以 a 和 b 系统的动量不守恒；a 离开墙后，a 和 b 系统水平方向不受外力，系统动量守恒。

 

4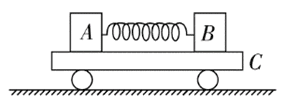．如图所示，A、B 两物体质量之比 m_A∶m_B = 3∶2，原来静止在平板小车 C 上，A、B 间有一根被压缩的弹簧，水平地面光滑。当弹簧突然释放后，则（     ）

A．若 A、B 与平板车上表面间的动摩擦因数相同，A、B 组成的系统动量守恒

B．若 A、B 与平板车上表面间的动摩擦因数相同，A、B、C 组成的系统动量守恒

C．若 A、B 所受的摩擦力大小相等，A、B 组成的系统动量守恒

D．若 A、B 所受的摩擦力大小相等，A、B、C 组成的系统动量守恒

【答案】

BCD

【解析】

如果 A、B 与平板车上的动摩擦因数相同，弹簧释放后 A、B 分别相对小车向左、向右滑动，它们所受摩擦力 F_A 向右，F_B 向左。由于 m_A∶m_B = 3∶2，所以 F_A∶F_B = 3∶2，则 A、B 所组成的系统所受合外力不为零，故其动量不守恒。对 A、B、C 组成的系统，A、B 与 C 间的摩擦力为内力，该系统所受合外力为零，故该系统的动量守恒。若 A、B 所受的摩擦力大小相等，则 A、B 组成的系统合外力为零，故动量守恒，B、C、D 正确。

 

5．甲、乙两名滑冰运动员沿同一直线相向运动，速度大小分别为 3 m/s 和 1 m/s，迎面碰撞后（正碰）甲、乙两人反向运动，速度大小均为 2 m/s，则甲、乙两人质量之比为（    ）

A．2∶3         B．2∶5          C．3∶5          D．5∶3

【答案】

C

【解析】

两人碰撞过程系统动量守恒，以甲的初速度方向为正方向，由动量守恒定律得

m_甲v_甲 + m_乙v_乙 = m_甲v_甲ʹ+ m_乙v_乙ʹ，

即 m_甲×3 + m_乙×（− 1） = m_甲×（− 2） + m_乙×2，

解得 m_甲∶m_乙 = 3∶5，故选项 C 正确。

 

6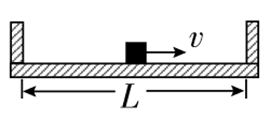．质量为 M、内壁间距为 L 的箱子静止于光滑的水平面上，箱子中间有一质量为 m 的小物块，小物块与箱子底板间的动摩擦因数为 μ。初始时小物块停在箱子正中间，如图所示。现给小物块一水平向右的初速度 v，小物块与箱壁碰撞 N 次后恰又回到箱子正中间，并与箱子保持相对静止。设碰撞都是弹性的，则整个过程中，系统损失的动能为（    ）

A．\(\frac{1}{2}\)mv²               B．\(\frac{{mM}}{{2(m + M)}}\)v²             C．\(\frac{1}{2}\)NμmgL         D．NμmgL

【答案】

BD

【解析】

由于水平面光滑，一方面，箱子和物块组成的系统动量守恒，二者经多次碰撞后，保持相对静止，易判断二者具有向右的共同速度 v′，根据动量守恒定律有 mv = （M + m）v′，系统损失的动能为 ΔE₁ = \(\frac{1}{2}\)mv² − \(\frac{1}{2}\)（M + m）v′²，可知 B 正确；另一方面，系统损失的动能可由 Q = ΔE_k 且 Q = μmg·s_相对 求得，由于小物块从中间向右出发，最终又回到箱子正中间，其间共发生 N 次碰撞，则 s_相对 = NL，则 D 选项也正确。

 

7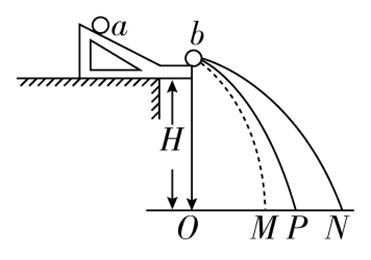．在用如图所示的装置做“探究碰撞中的不变量”实验时，入射球 a 的质量为 m₁，被碰球 b 的质量为 m₂，小球的半径为 r，各小球的落地点如图所示，下列关于这个实验的说法中正确的是（    ）

A．入射球与被碰球最好采用大小相同、质量相同的小球

B．让入射球与被碰球连续 10 次相碰，每次都要使入射小球从斜槽上不同的位置滚下

C．要验证的表达式是 m₁·ON = m₁·OM + m₂·OP

D．要验证的表达式是 m₁·OP = m₁·OM + m₂·ON

【答案】

D

【解析】

入射球与被碰球应采用体积等大的球，但入射球的质量应大于被碰球的质量，故 A 错；为保证入射小球每次都以等大的速度碰撞被撞小球，每次都要使入射小球从斜槽上相同位置滚下，B 错；图中 OP 为入射小球 a 没与 b 球碰撞时落地的射程，OM 为 a 球与 b 球碰后 a 球落地的射程，ON 为 b 球被撞后落地的射程，故要验证的表达式是：m₁·OP = m₁·OM + m₂·ON，C 错误，D 正确。

 

8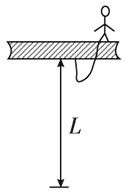．如图所示，一高空作业的工人重为 600 N，系一条长为 L = 5 m 的安全带，若工人不慎跌落时安全带的缓冲时间 t = 1 s，则安全带受的冲力是多少？（g 取 10 m/s²）

【答案】

1200 N，方向竖直向下

 

9．如图所示，把重物 G 压在纸带上，用一水平力 F 缓慢拉动纸带，重物跟着纸带一起运动；若迅速拉动纸带，纸带将会从重物下抽出。对这种现象的解释正确的是（    ）

A．在缓慢拉动纸带时，纸带对重物的摩擦力大

B．在迅速拉动纸带时，纸带对重物的摩擦力小

C．在缓慢拉动纸带时，纸带对重物的冲量大

D．在迅速拉动纸带时，纸带对重物的冲量小

【答案】

CD

【解析】

由重物的动量定理得 fΔt = Δp，不管是缓慢拉动纸带还是迅速拉动纸带，f 都是滑动摩擦力，是恒定不变的力，缓慢拉动时，作用时间长，纸带对重物的冲量大，重物动量的变化量大，运动状态变化明显，重物跟着纸带一起运动。迅速拉动时，作用时间短，纸带对重物的冲量小，重物动量的变化量小，运动状态几乎不变，纸带从重物下抽出，所以 A、B 选项都不正确，而 C、D 选项是正确的。

 

10．为估算池中睡莲叶面承受雨滴撞击产生的平均压强，小明在雨天将一圆柱形水杯置于露台，测得 1 小时内杯中水位上升了 45 mm。查询得知，当时雨滴竖直下落的速度约为 12 m/s，据此估算该压强约为（设雨滴撞击睡莲后无反弹，不计雨滴重力，雨水的密度为 1 × 10³ kg/m³）（     ）

A.0.15 Pa                 B．0.54 Pa              C．1.5 Pa                D．5.4 Pa

【答案】

A

【解析】

1 小时内雨的总质量 m = ρSh，对水列动量定理，向上为正方向，Ft = 0 − （− mv），再由压强公式 p = \(\frac{F}{S}\)，得 p = \(\frac{{\rho hv}}{t}\)，代入数据得 p = 0.15 Pa。A 选项正确。

 

11．如图所示，质量为 m = 245 g 的物块（可视为质点）放在质量为 M = 0.5 kg 的木板左端，足够长的木板静止在光滑水平面上，物块与木板间的动摩擦因数为 μ = 0.4。质量为 m₀ = 5 g 的子弹以速度 v₀ = 300 m/s 沿水平方向射入物块并留在其中（时间极短），g 取 10 m/s²。子弹射入后，求：

（1）物块相对木板滑行的时间；

（2）物块相对木板滑行的位移。

【答案】

（1）1 s

（2）3 m

【解析】

（1）子弹打入木块过程，由动量守恒定律得

m₀v₀ = （m₀ + m）v₁

木块在木板上滑动过程，由动量守恒定律得

（m₀ + m）v₁ = （m₀ + m + M）v₂

对子弹木块整体，由动量定理得

－ μ（m₀ + m）gt = （m₀ + m）（v₂－v₁）

联立解得物体相对小车的滑行时间 t = \(\frac{{{v_2} - {v_1}}}{{ - \mu g}}\) = 1 s

（2）由能量守恒定律得

μ（m₀ + m）gd = \(\frac{1}{2}\)（m₀ + m）v₁² − \(\frac{1}{2}\)（m₀ + m + M）v₂²

联立解得 d = 3 m

 

12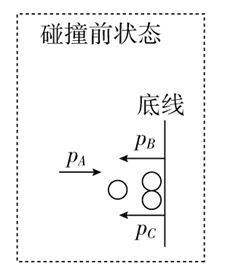．如图所示，在橄榄球比赛中，一个 85 kg 的前锋队员以 5 m/s 的速度跑动，想穿越防守队员到底线触地得分。就在他刚要到底线时，迎面撞上了对方两名均为 65 kg 的队员，一个速度为 2 m/s，另一个速度为 4 m/s，然后他们就扭在了一起，则（    ）

A．他们碰撞后的共同速率是 0.2 m/s

B．碰撞后他们动量的方向仍向前

C．这名前锋能得分

D．这名前锋不能得分

【答案】

BC

【解析】

取前锋队员跑动的速度方向为正方向，根据动量守恒定律可得：Mv_A + mv_B + mv_C = （M + m + m）v，其中 v_A = 5 m/s，v_B = − 2 m/s，v_C = − 4 m/s，代入数据得：v ≈ 0.16 m/s。所以碰撞后的速度仍向前，故这名前锋能得分，B、C两项正确。

 

13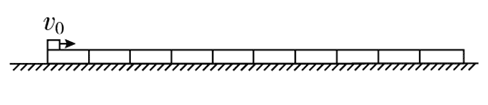．如图所示，光滑水平地面上依次放置着质量 m = 0.08 kg 的 10 块完全相同的长直木板。一质量 M = 1.0 kg、大小可忽略的小铜块以初速度 v₀ = 6.0 m/s 从长木板左侧滑上木板，当铜块滑离第一块木板时，速度大小为 v₁ = 4.0 m/s。铜块最终停在第二块木板上。（取 g = 10 m/s²，结果保留两位有效数字）求 ：

（1）第一块木板的最终速度的大小；

（2）铜块的最终速度的大小。

【答案】

（1）2.5 m/s

（2）3.4 m/s

【解析】

（1）铜块和 10 个木板组成的系统水平方向不受外力，所以系统动量守恒，设铜块刚滑到第二块木板时，第一块木板的速度为 v₂，由动量守恒得，

Mv₀ = Mv₁ + 10mv₂

得 v₂ = 2.5 m/s。

（2）由题可知铜块最终停在第二块木板上，设铜块的最终速度为 v₃，由动量守恒得：Mv₁ + 9mv₂ = （M + 9m）v₃

得 v₃ = 3.4 m/s。

 

14．两个小球 A、B 在光滑水平面上沿同一直线运动，其动量大小分别为 5 kg·m/s 和 7 kg·m/s，发生碰撞后小球 B 的动量大小变为10 kg·m/s，由此可知：两小球的质量之比可能为（    ）

A．\(\frac{{{m_{\rm{A}}}}}{{{m_{\rm{B}}}}}\) = 1              B．\(\frac{{{m_{\rm{A}}}}}{{{m_{\rm{B}}}}}\) = \(\frac{1}{2}\)             C．\(\frac{{{m_{\rm{A}}}}}{{{m_{\rm{B}}}}}\) = \(\frac{1}{5}\)            D．\(\frac{{{m_{\rm{A}}}}}{{{m_{\rm{B}}}}}\) = \(\frac{1}{10}\)

【答案】

C

 

15．在光滑水平面上，动能 E_k0，动量的大小为 p₀ 的小钢球 1 与静止小钢球 2 发生碰撞，碰撞前后球 1 的运动方向相反，将碰撞后球 1 的动能和动量大小分别记为 E_k1、p₁，球 2 的动能和动量的大小分别记为 E_k2、p₂，则必有（    ）

A．E_k1 < E_k0                   B．p₁ < p₀                       C．E_k2 > E_k0                 D．p₂ > p₀

【答案】

ABD

【解析】

两个小钢球在相碰过程中同时遵守能量守恒和动量守恒，由于外界没有能量输入，而碰撞中可能产生热量，所以碰撞后的总动能不会超过碰撞前的总动能，即 E_k1 + E_k2 ≤ E_k0，A 选项正确，C 选项错误。另外，A 选项也可写成 \(\frac{{p_1^2}}{{2m}}\) < \(\frac{{p_0^2}}{{2m}}\)，因此 B 选项正确。根据动量守恒，设球 1 原来的运动方向为正方向，有p₂ − p₁ = p₀，所以 D 选项正确。

 

16．光滑水平轨道上有三个木块 A、B、C，质量分别为 m_A = 3m、m_B = m_C = m，开始时 B、C 均静止，A 以初速度 v₀ 向右运动，A 与 B 碰撞后分开，B 又与 C 发生碰撞并粘在一起，此后 A 与 B 间的距离保持不变。求 B 与 C 碰撞前 B 的速度大小。

【答案】

\(\frac{6}{5}\)v₀

【解析】

设 A 与 B 碰撞后，A 的速度为 v_A，B 与 C 碰撞前 B 的速度为 v_B，B 与 C 碰撞后粘在一起的速度为 v，由动量守恒定律得

对 A、B 木块：m_Av₀ = m_Av_A + m_Bv_B①

对 B、C 木块：m_Bv_B = （m_B + m_C）v②

由 A 与 B 间的距离保持不变可知

v_A = v③

联立①②③式，代入数据得

v_B = \(\frac{6}{5}\) v₀。

 

17．载人气球静止于高 h 的空中，气球的质量为 M，人的质量为 m，若人沿绳梯滑至地面，则绳梯至少为多长？

【答案】

\(\frac{{M + m}}{M}\) h

【解析】

气球和人原来静止在空中，说明系统所受合外力为零，故系统在人下滑过程中动量守恒，人着地时绳梯至少应接触地面，设绳梯长为 L，人沿绳梯滑至地面，人的位移为 x_人，球的位移为 x_球，它们的位移状态图如图所示，

由平均动量守恒有：0 = Mx_球 − mx_人，

又有x_球 + x_人 = L，x_人 = h，故L = \(\frac{{M + m}}{M}\) h。