0．如图所示，质量为 m 的导体棒 ab 垂直圆弧形金属导轨 MN、PQ 放置，导轨下端接有电源，导体棒与导轨接触良好，不计一切摩擦。现欲使导体棒静止在导轨上，则下列方法可行的是（    ）

（A）施加一个沿 ab 方向的匀强磁场

（B）施加一个沿 ba 方向的匀强磁场

（C）施加一个竖直向下的匀强磁场

（D）施加一个竖直向上的匀强磁场

【答案】

C

【解析】

施加一个沿 ab 方向的匀强磁场或 ba 方向的匀强磁场，导体棒都不受安培力，不可能静止在导轨上，则 A、B 错；由 b 看向 a 时，施加一个竖直向下的匀强磁场，由左手定则可知导体棒所受安培力方向水平向右，可能静止在导轨上，则 C 对；由 b 看向 a 时，施加一个竖直向上的匀强磁场，由左手定则可知，导体棒所受安培力方向水平向左，不可能静止在导轨上，则 D 错。

 

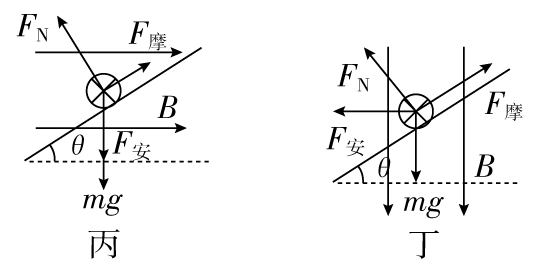
0．质量为 m 的金属细杆置于倾角为 θ 的导轨上，导轨的宽度为 d，杆与导轨间的动摩擦因数为 μ，有电流通过杆，杆恰好静止于导轨上，在如图所示的 A、B、C、D 四个图中，杆与导轨间的摩擦力一定不为零的是（    ）

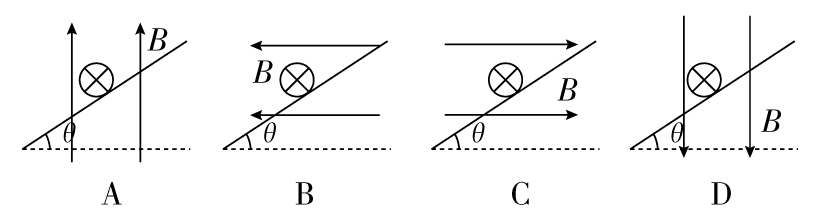
【答案】

CD

【解析】

 

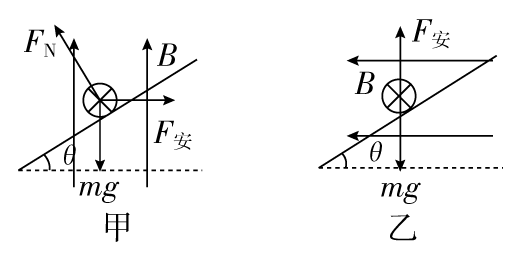
1．1．磁场中某点磁感应强度的大小，跟放在该点的试探电流元的情况无关。（    ）

2．磁场中某点磁感应强度的方向，跟放在该点的试探电流元所受磁场力的方向一致。（    ）

3．磁感线是客观存在的，磁感线上各点的切线方向表示该点的磁场方向。（    ）

4．通电导线放入磁场中，若不受安培力，说明该处磁感应强度为零。（    ）

5．垂直放置在磁场中的线圈面积减小时，穿过线圈的磁通量可能增大。（    ）

6．安培力可以做正功，也可以做负功。（    ）

【答案】

1．√     2．×     3．×     4．×     5．√     6．√

 

2．关于磁感应强度，下列说法中正确的是（     ）

（A）由 B = \(\frac{F}{{IL}}\) 可知，B 与 F 成正比，与 IL 成反比

（B）通电导线放在磁场中的某点，那点就有磁感应强度，如果将通电导线拿走，那点的磁感应强度就为零

（C）通电导线不受安培力的地方一定不存在磁场，即 B = 0

（D）磁场中某一点的磁感应强度由磁场本身决定，其大小和方向是唯一确定的，与通电导线无关

【答案】

D

【解析】

磁场中某点磁感应强度是由磁场本身决定的，与是否放入通电导线无关，与通电导线在磁场中是否受力无关，D 正确。

 

3．磁场中某区域的磁感线如图所示，则（    ）

（A）a、b 两处的磁感应强度的大小不等，B_a > B_b

（B）a、b 两处的磁感应强度的大小不等，B_a < B_b

（C）同一通电导线放在 a 处受力一定比放在 b 处受力大

（D）同一通电导线放在 a 处受力一定比放在 b 处受力小

【答案】

B

【解析】

磁感线的疏密程度表示磁感应强度的大小，由图可知，b 处的磁感线比 a 处的密，所以 B_a < B_b；导线放在磁场中的受力与导线放置的方向有很大关系，而不是仅仅取决于 B 与 I 的大小。故正确答案为 B。

 

4．如图所示，三根长直通电导线中电流大小相同，通电电流方向为：b 导线和 d 导线中电流向纸内，c 导线中电流向纸外，a 点为 b、d 两点连线的中点，ac 垂直于 bd，且ab = ad = ac。则a点的磁场方向为（    ）

（A）垂直纸面指向纸外            （B）垂直纸面指向纸内

（C）沿纸面由 a 指向 b          （D）沿纸面由 a 指向 d

【答案】

C

【解析】

b、d 两导线电流在 a 处的磁感应强度大小相等、方向相反，互相抵消，故 a 处磁场方向决定于直线电流 c。由安培定则可知，a 处磁场方向为 a → b。故正确答案为 C。

 

5．在如图所示的四幅图中，正确标明通电导线所受安培力F方向的是（    ）

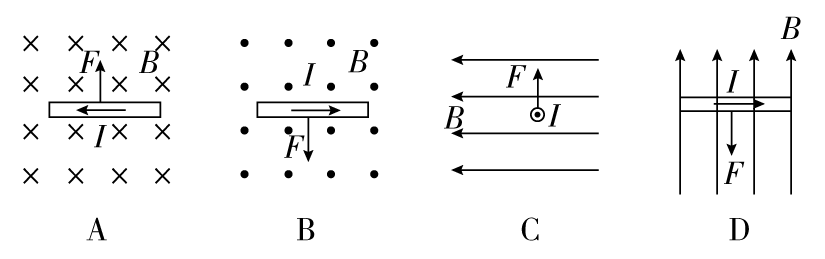
【答案】

B

【解析】

依据左手定则知 B 正确。

 

6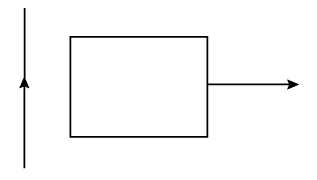．如图所示，通电直导线右边有一个矩形线框，线框平面与直导线共面，若使线框逐渐远离（平动）通电导线，则穿过线框的磁通量将（    ）

（A）逐渐增大            （B）逐渐减小

（C）保持不变            （D）不能确定

【答案】

B

【解析】

离导线越远，电流产生的磁场越弱，穿过线圈的磁感线条数越少，磁通量逐渐减小，故只有 B 正确。

 

6．如图所示，一矩形线圈 abcd 放置在匀强磁场中，并绕过 ab、cd 中点的轴 OO′ 以角速度 ω 逆时针匀速转动（沿着 OO′ 轴观察）。若以线圈平面与磁场夹角 θ = 0° 时（如图）为计时起点，并规定当电流自 a 流向 b 时电流方向为正。则下列四幅图中正确的是（    ）

 

【答案】

D

【解析】

矩形线圈在匀强磁场中绕垂直于磁场方向的轴转动时，由于 t = 0 时，线圈的转动方向如题图，由楞次定律判断可得，线圈中电流方向为 a→d→c→b→a，与规定的电流正方向相反，电流为负值。又因为此时产生的感应电流最大，故只有选项 D 正确。

 

7．倾角为 α 的导电轨道间接有电源，轨道上放有一根静止的金属杆 ab。现垂直轨道平面向上加一匀强磁场，如图所示，磁感应强度 B 由零逐渐增大的过程中，ab 杆受到的静摩擦力（    ）

（A）逐渐增大                   （B）逐渐减小

（C）先增大后减小            （D）先减小后增大

【答案】

D

【解析】

开始时，摩擦力沿轨道向上，在磁感应强度 B 逐渐增大的初始阶段，金属杆 ab 的受力如图所示。由力的平衡知：

F_f + BIL = mgsinα，故 B 增大时，F_f 减小。

当 BIL = mgsinα 时，F_f = 0。

当 B 继续增大时，F_f 方向沿斜面向下，故 BIL = mgsinα + F_f，故 B 增大时，F_f 增大，选项 D 正确。

 

8．已知长直通电导线在周围某点产生磁场的磁感应强度大小与电流成正比、与该点到导线的距离成反比。4 根电流相同的长直通电导线 a、b、c、d 平行放置，它们的横截面的连线构成一个正方形，O 为正方形中心，a、b、c 中电流方向垂直纸面向里，d 中电流方向垂直纸面向外，则 a、b、c、d 长直通电导线在 O 点产生的合磁场的磁感应强度 B（     ）

（A）大小为零

（B）大小不为零，方向由 O 指向 d

（C）大小不为零，方向由 O 指向 c

（D）大小不为零，方向由 O 指向 a

【答案】

D

【解析】

由安培定则可知，a、c 中电流方向相同，两导线在 O 处产生磁场的磁感应强度大小相等、方向相反，合矢量为零；b、d 两导线中电流方向相反，由安培定则可知，两导线在 O 处产生的磁场的磁感应强度方向均由 O 指向 a，故 D 选项正确。

 

9．如图所示，M、N 和 P 是以 MN 为直径的半圆弧上的三点，O 为半圆弧的圆心，∠MOP = 60°，在M、N 处各有一条长直导线垂直穿过纸面，导线中通有大小相等的恒定电流，方向如图所示，这时 O 点的磁感应强度大小为 B₁，若将 N 处长直导线移至 P 处，则 O 点的磁感应强度大小为 B₂，那么 B₂ 与 B₁ 之比为（     ）

（A）1∶1            （B）1∶2            （C）\(\sqrt 3 \)∶1      （D）\(\sqrt 3 \)∶2

【答案】

B

【解析】

如图所示，当通有电流的长直导线在 M、N 两处时，根据安培定则可知，二者在圆心 O 处产生的磁感应强度的大小都为 \(\frac{{{B_1}}}{2}\)；当 N 处长直导线移至 P 处，两导线在圆心 O 处产生的磁感应强度的大小也为 \(\frac{{{B_1}}}{2}\)，作平行四边形，由几何关系得 B₂ = \(\frac{{{B_1}}}{2}\)，那么 \(\frac{{{B_2}}}{B_1}\)  = \(\frac{{{1}}}{2}\)，故选项 B 正确。

 

10．已知通电长直导线周围某点的磁感应强度 B = k \(\frac{I}{r}\)，即磁感应强度 B 与导线中的电流 I 成正比、与该点到导线的距离r成反比。如图所示，两根平行长直导线相距为 R，通以大小、方向均相同的电流。规定磁场方向垂直纸面向里为正，在 0～R 区间内磁感应强度 B 随 r 变化的图线可能是（    ）

【答案】

C

【解析】

由安培定则可知在两根平行长直导线上的电流在其间产生的磁场方向相反，再由 B = k \(\frac{I}{r}\) 可得在其连线的中点上两电流产生的磁感应强度是等大反向的，即合场强为零，则 A、B 均错。在靠近左导线处，左电流产生的磁场要强于右电流产生的磁场，则合场强的方向是垂直纸面向里的，即为正；同理，在靠近右导线处，合场强的方向是垂直纸面向外的，即为负，所以 C 对、D 错。

 

11．将长为 l 的导线弯成 \(\frac{1}{6}\)  圆弧，固定于垂直纸面向外、大小为 B 的匀强磁场中，两端点 A、C 连线竖直，如图所示。若给导线通以由 A 到 C、大小为 I 的恒定电流，则导线所受安培力的大小和方向是（     ）

（A）IlB，水平向左           （B）IlB，水平向右

（C）\(\frac{{3IlB}}{\pi }\)，水平向左         （D）\(\frac{{3IlB}}{\pi }\)，水平向右

【答案】

C

 

12．如图所示，一个边长为 l、三边电阻相同的正三角形金属框放置在磁感应强度为 B 的匀强磁场中。若通以图示方向的电流（从 A 点流入，从 C 点流出），电流为I，则金属框受到的磁场力为（    ）

（A）0                 （B）IlB

（C）\(\frac{4}{3}\)IlB           （D）2IlB

【答案】

B

 

15．如图所示，用两根轻细金属丝将质量为 m、长为 l 的金属棒 ab 的两端悬挂在c、d 两处，置于竖直向上的匀强磁场内。当棒中通以从 a 到 b 的电流 I 后，两悬线偏离竖直方向 θ 角处于平衡状态，则磁感应强度 B 为多大？为了使棒平衡在该位置上，所需匀强磁场的磁感应强度 B 最小为多少，方向如何？

【答案】

\(\frac{{mg}}{{Il}}\)tanθ，\(\frac{{mg}}{{Il}}\)sinθ，方向平行于悬线向上

【解析】

首先要对研究对象进行受力分析，画出受力分析图（如侧视图、俯视图），然后根据平衡条件列方程并分析极值。

 

画出从右侧逆着电流方向的侧视图，如图甲所示。金属棒在重力 mg、悬线拉力 T、安培力 F 三个力作用下处于平衡状态，由平衡条件得 F = mgtanθ

又 F = BIl，解得 B = \(\frac{{mg}}{{Il}}\)tanθ

要求所加匀强磁场的磁感应强度最小，应使棒在该位置平衡时所受的安培力最小。由于棒的重力恒定，悬线拉力的方向不变，由如图乙所示的力三角形可知，安培力的最小值为 F_min = mgsinθ

即 B_minIl = mgsinθ

解得 B_min = \(\frac{{mg}}{{Il}}\)sinθ

由左手定则可知，所加磁场的方向应平行于悬线向上。