1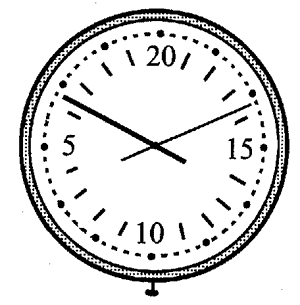．如图所示是篮球比赛专用计时器，请你根据图中提供的信息，计算计时器正常工作时指针转动的角速度。

【答案】

分针的角速度ω≈5.2×10^-3 rad/s

秒针的角速度ω≈0.105 rad/s

 

2．关于匀速圆周运动，下列不正确的说法是（     ）。

（A）匀速圆周运动是速度不变的运动

（B）匀速圆周运动是速度不断变化的运动

（C）做匀速圆周运动的物体所受合外力一定不为零

（D）匀速圆周运动也是曲线运动

【答案】

A

 

3．举出三个与圆周运动有关的体育运动项目。

【答案】

自由体操、链球、单双杠等

 

4．飞机在空中与水平面平行的平面上做匀速圆周运动，圆周半径为4000 m。如果飞机的线速度是80 m/s，则飞机绕一圈要多少时间？飞机的角速度是多大？

【答案】

t＝314 s，ω＝0.02 rad/s

 

5．估算上海锦江乐园“摩天轮”在正常运行时，轿箱内游客的角速度和和线速度。（位于上海市锦江乐园的摩天轮，它的高度为108 m，直径98 m，每次可乘坐378人，坐在轿厢内的游客转一圈需25 min。）

【答案】

ω＝4.19×10^-3 rad/s，v＝0.2 m/s

 

6．钟表的时针、分针和秒针的针尖都可认为在做匀速圆周运动，它们的角速度之比是______，图中秒针针尖到转轴的距离是15 cm，它转一周经过的路程是______m，它的线速度大小是_______m/s。

【答案】

1∶12∶720，0.942，0.0157

 

7．直径为40 m的旋转餐厅缓慢转动一周需100 min，则离窗边2 m的顾客的线速度大小为________m/s，坐在窗边的顾客的线速度大小为_______m/s，他们的角速度之比为________。

【答案】

1.9×10^-2，2.1×10^-2，1∶1

 

8．我国发射的第一颗人造地球卫星“东方红一号”绕地球近似做匀速圆周运动一周所需时间为114 min，离地面平均高度是1412 km。计算卫星环绕地球运行时线速度的大小和角速度的大小。（地球半径为6400 km ）

【答案】

7.19×10³ km/s，9.2×10^-4 rad/s

 

9．请你利用表格，对线速度和角速度的定义、定义式、单位等作出比较。

【答案】

	定义	定义式	单位
线速度	质点经过的圆弧长度s与所用时间t之比	v＝\(\frac{s}{t}\)	m/s
角速度	质点所在半径转过的角度φ与所用时间t之比	ω＝\(\frac{\varphi }{t}\)	rad/s
比较	都描述圆周运动的快慢，线速度从质点移动的快慢来描述，角速度从质点所在半径转动的快慢来描述	线速度定义式包含长度，角速度定义式包含弧度	m是长度单位，rad是弧度单位

 

10．对于一个匀速转动的物体，下面说法中正确的是（     ）。

（A）物体上任何一点的线速度不变

（B）物体上不同点的线速度的大小都不同

（C）物体上任何一点的角速度大小都不变

（D）物体上不同的点角速度的大小都不同

【答案】

C

 

11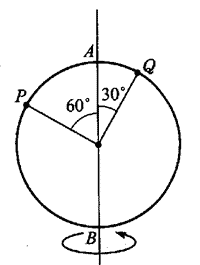．如图所示，一个圆环以直径AB为轴做匀速转动，则环上P、Q两点的角速度大小之比ω_P∶ω_Q＝__________。

【答案】

1∶1

 

12．地球可以看作一个球体，则在上海地面的物体随地球自转的角速度为_________rad/s。

【答案】

7.3×10^-5

 

13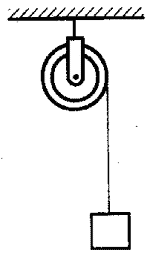．一个半径为4 cm的定滑轮，绕有多圈细绳，细绳的一端固定在定滑轮上，另一端与重物相连，如图所示。设重物以2 m/s²的加速度由静止匀加速下落，当重物下落距离为1 m时，求滑轮边上一点转动的线速度和滑轮转过的周数。

【答案】

2 m/s，3.98 圈

 

14．单缸发动机的飞轮每分转2400 转，求：

（1）飞轮转动的周期与角速度。

（2）若飞轮上某点离轴线的距离r为0.2 m，则该点的线速度是多少？

【答案】

（1）T＝0.025 s

ω≈251 rad/s

（2）v＝50.2 m/s

 

15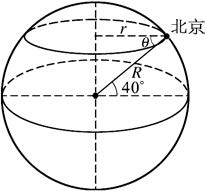．地球可看成是半径为6400 km的球体，北京的地理纬度大约是北纬40°，则在北京地面上的物体随地球自转的线速度是多少？角速度是多少？（已知cos40°＝0.766 ）

【答案】

ω≈7.2×10^-5 rad/s

v≈353 m/s

 

16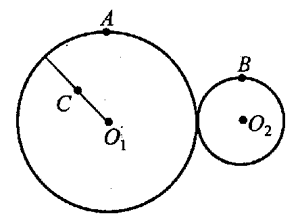．如图所示，O₁、O₂两轮依靠摩擦传动而不打滑，O₁轮的半径是O₂轮的2倍。A、B分别为大、小轮边缘上的点，C为大轮上一条半径的中点。试分别讨论A、B、C三点的角速度、线速度的关系。

【答案】

v_A＝v_B＝2v_C

ω_B＝2ω_A＝2ω_C

 

17．关于两个做匀速圆周运动的质点，正确的说法是（    ）

（A）角速度大的线速度一定大

（B）角速度相等，线速度一定也相等

（C）半径大的线速度一定大

（D）周期相等，角速度一定相等

【答案】

D

 

18．在半径为15 m的圆形杂技场进行马术表演时，马沿着场地边缘奔跑，把马的运动看成是匀速圆周运动，马的线速度是8 m/s，求马的运动周期、转速和角速度。

【答案】

T＝11.78 s，n＝5.1 r/min，ω＝0.53 rad/s

 

19．砂轮机在磨削金属时，砂轮和金属的碎屑因摩擦产生的高温形成火星，你注意到火星沿什么方向飞行？如果砂轮的半径是10 cm，转速是1080 r/min，火星刚飞出时的速度是多少？砂轮上半径为5 cm处质点的角速度是多少？

【答案】

沿砂轮切线方向飞出，v＝11.3 m/s，ω＝113 rad/s

 

20．在一个匀速转动物体上，轴线外的各点都在做______运动，描述各点运动快慢的物理量中相同的是_____________，可能不同的是____________，只有____相同的各点，描述运动快慢的物理量大小才相同。

【答案】

圆周运动，角速度、周期、转速，线速度，半径

 

21．若全自动洗衣机脱水时桶的转速为1200 r/min，桶的半径为20 cm，则桶壁任一点的角速度为_____rad/s，线速度为_____m/s。

【答案】

125.6，25.12

 

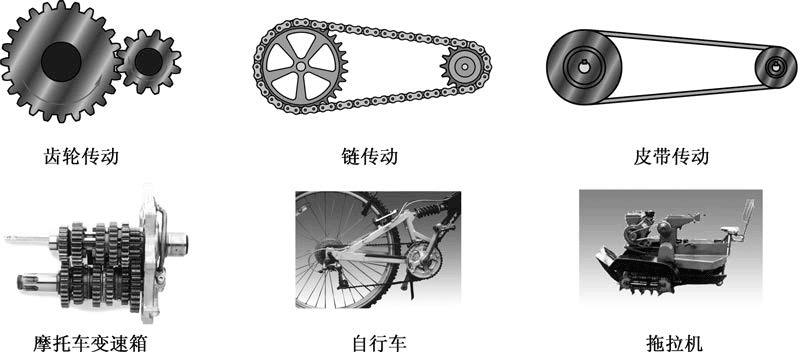
22．传动机构就是传递运动、动力和能量的机构，机械传动的主要方式有齿轮传动、链传动、皮带传动，前两种传动依靠齿与齿、齿与链的啮合推力，后一种则依赖于摩擦力。如图表示传动的原理和应用，请观察图片，举出三种传动方式的其他实例。

【答案】

齿轮传动如手摇钻；链传动如摩托车；皮带传动如缝纫机

 

23．如图所示为一皮带传动装置，右轮的半径为r，a是它边缘上的一点。左轮是一个轮轴，轮半径为4r，轴半径为2r，b点在轴上，到轴心的距离为r，c点和d点分别在轴和轮的边缘。若在传动过程中皮带不打滑，则正确结论是（    ）。

（A）a点与b点的线速度大小相等

（B）a点与b点的角速度大小相等

（C）a点与c点的线速度大小相等

（D）a点与d点的角速度大小相等

【答案】

C

 

24．三个在地球表面静止的物体A、B、C分别放在北京、上海和广州，则它们角速度ω_A、ω_B、ω_C三者的大小关系是______，线速度v_A、v_B、v_C三者的大小关系是______，周期T_A、T_B、T_C三者的大小关系是________。

 

【答案】

ω_A＝ω_B＝ω_C，v_A＜v_B＜v_C，T_A＝T_B＝T_C

 

25．如图所示，有一个偏心轮绕O点匀角速转动，O点不在圆心，试找出偏心轮上：

（1）位于轮缘线速度最大的点。

（2）位于轮缘线速度最小的点。

（3）线速度大小相同的点。

（4）角速度相同的点。

【答案】

（1）线速度最大的点在过O点的直径离O点的远端

（2）线速度最小的点在过O点的直径离O点的近端

（3）没有线速度大小相同的点？？

（4）除O点外各点角速度都相同

 

26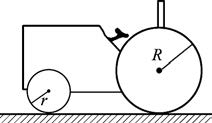．如图所示，拖拉机前面导轮的半径r只有后面主动轮半径R的一半，则前后两轮边缘上点的线速度之比为______，角速度之比为_______。

【答案】

1∶1，2∶1

 

27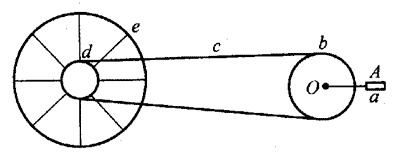．如图所示为自行车传动部分示意图，a为踏脚，OA为曲轴，b为齿轮（牙盘），d为齿轮（飞），c为链条，e为后轮（主动轮）。已知OA＝25 cm，r_b＝10 cm，r_d＝4 cm，r_e＝36 cm。如果传动过程中无打滑现象，当踏脚以每分30转的速度匀速转动时，自行车行进的速度为______m/s。

【答案】

2.83

 

28．机械手表中的分针与秒针可视为匀速转动。请你仔细观察一下，分针与秒针从第一次重合至第二次重合，中间经历的时间最接近（    ）。

（A）59 s                           （B）60 s

（C）61 s                           （D）与分针位置有关的一个变量

【答案】

C

 

29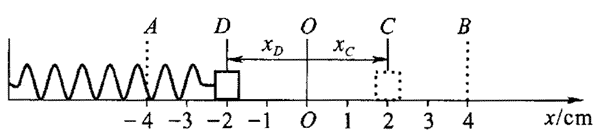．对图所示的弹簧振子的振动过程，回答以下问题：

（1）当振子接连先后两次经过同一位置C点时的位移、回复力以及加速度是否相同？

（2）当振子接连先后经过与平衡位置O对称的C、D两点时上述物理量是否相同？

（3）当振子由平衡位置向最大位移处运动时，以上各物理量如何变化？

【答案】

（1）经过同一位置时，振子的位移、回复力、加速度等矢量相同；速度大小相等、方向相反。

（2）振子先后经过对称点C、D时，位移、回复力、加速度等矢量的大小相等、方向相反；速度矢量相同。

（3）振子由平衡位置向最大位移处运动时，振子的位移、回复力、加速度将增大，速度减小，所以做的是变加速运动。

 

30．将一水平放置的弹簧振子从平衡位置 O 向右拉开 4 cm 后放手，让它做振动。已知从放手到回到平衡位置的时间为 0.1 s，求：

（1）弹簧振子的振幅、周期、频率。

（2）2 s 内完成全振动的次数。

（3）振子从开始运动经 2.5 s 末的位移大小。此时正要向哪个方向做怎样的运动？

（4）振子经 5 s 通过的路程。

（5）若将弹簧振子从平衡位置向右拉开 6 cm 后释放，运动过程中的振幅、周期、频率变为多大？

【答案】

（1）振幅大小为4 cm；周期为0.4 s；频率为2.5 Hz。

（2）5次全振动。

（3）位移大小为零，正向左做加速度增大的减速运动。

（4）通过的路程为2 m。

（5）振幅为6 cm，而周期与频率均不变。

 

31．下列运动中可以看作机械振动的是（    ）。

（A）声带发声                   （B）音叉被移动

（C）火车沿斜坡行驶        （D）秋风中树叶落下

【答案】

A

 

32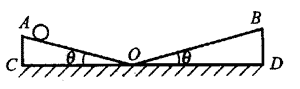．如图所示，小球的质量为m，在重力和斜面弹力的作用下沿着两个倾角为θ的对称、光滑的斜面OA和OB做往复运动。判断小球是否做机械振动，并说明理由。

【答案】

在做机械振动，因为小球受回复力作用不断在O点左右沿斜面上下运动，运动的最大高度不变，保证往复运动持续不断

 

33．下列物理量中：

（1）描述物体振动快慢的是（    ）。

（2）描述物体振动强弱的是（    ）。

（A）频率            （B）回复力        （C）振幅            （D）速度

【答案】

A，C

 

34．一个做机械振动的物体，由平衡位置向最大位移处运动时，下列说法正确的是（     ）。

（A）物体的位移逐渐变大        （B）物体的速度逐渐变大

（C）物体的回复力逐渐变小     （D）物体的周期逐渐变小

【答案】

A

 

35．一般人耳能听到的声音振动频率下限约为20 Hz，上限约为20000 Hz。问相应的周期是多少？

【答案】

0.05 s，5×10^-5 s

 

36．振动的物体在1.2 s时间内完成了30次全振动，求它的振动周期和频率。

【答案】

0.04 s，25 Hz

 

37．假设蚊子翅膀振动的频率为400 Hz，翅尖振幅为0.5 mm。问1 s内蚊子翅尖由于振动所经过的路程是多少？

【答案】

0.8 m

 

38．设弹簧振子的振幅为0.1 m，周期为4 s，弹簧原长为0.5 m，而且开始时小球位于最左的位置，初速为零。经过3.5个周期的瞬时，小球位于何处？此时小球相对于平衡位置的位移是多少？相对于出发点的位移又是多少？弹簧总长度是多少？在这3.5个周期内，小球经过的路程是多少？

【答案】

经3.5个周期，振子位于最右的位置；相对平衡位置的位移为0.1 m；相对出发点的位移为0.2m，方向向右；弹簧总长度0.6 m；3.5个周期中，振子经过的路程为1.4 m

 

39．判断下列说法的正误：

（1）在变力作用下的运动一定是机械振动。（    ）

（2）做机械振动的物体，其加速度的方向与位移的方向在每一时刻都相反。（    ）

（3）做机械振动的物体，速度增大时，加速度减小。（     ）

（4）振动物体两次经过平衡位置的过程叫一次全振动。（     ）

【答案】

（1）×（2）√（3）√（4）×

 

40．一弹簧振子做机械振动，若从平衡位置O开始计时，经过0.3 s时，振子第一次经过P点，又经过了0.2 s，振子第二次经过P点，则该弹簧振子的振动周期为（     ）。

（A）0.4 s            （B）0.8 s            （C）1.6 s            （D）1.4 s

【答案】

C

 

41．一弹簧振子做机械振动，若从平衡位置O开始计时，经过0.3 s时，振子第一次经过P点，又经过了0.2 s，振子第二次经过P点，则从振子第二次经过P点算起，该振子第三次经过P点所需的时间为（    ）

（A）4 s        （B）8 s        （C）3\(\frac{1}{3}\) s           （D）1.4 s

【答案】

D

 

42．将一水平放置的弹簧振子从平衡位置向右拉开1 cm后释放，振子做振动。若第一次到平衡位置的时间为0.1 s，则该振子的振幅为_____cm，周期为____s，频率为_____Hz，振子在1s内的路程为_______cm，在0.7 s末振子的位移大小为_____cm，正要向_____（选填“左”或“右”）做______（选填“加速”或“减速”）运动。

【答案】

1，0.4，2.5，10，0，右，减速

 

43．某弹簧振子做振动，先后以相同速度通过相距10 cm的A、B两点，历时0.2 s，再从B点回到A点的最短时间为0.4 s，则：

（1）平衡位置在何处？

（2）振子的运动周期及频率是多少？

【答案】

（1）AB的中点

（2）T＝0.8 s，f＝1.25 Hz

 

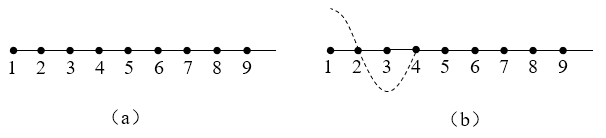
44．如图（a）所示的长绳中编号为1，2，…，8，9的一系列质点（相邻点的间距为a），相继振动起来，某时刻形成如图（b）中虚线所示的波形，即1号质点处于波峰位置时，3号质点恰好处于波谷位置，4号质点刚开始振动。又过一段时间，当1号质点第二次通过平衡位置时，波传到哪里？试画出这一时刻绳波的波形。

【答案】

如图（a）所示的长绳中编号为1，2，…，8，9的一系列质点（相邻点的间距为a），相继振动起来，某时刻形成如图（b）中虚线所示的波形，即1号质点处于波峰位置时，3号质点恰好处于波谷位置，4号质点刚开始振动。又过一段时间，当1号质点第二次通过平衡位置时，波传到哪里？试画出这一时刻绳波的波形。

【解析】

可先分析1号质点处于波峰位置，3号质点处于波谷，4号质点则开始振动时的波形，见图（b）中虚线A。可看出形成此段波所需时间为\(\frac{3}{4}\)T，波向前传了3a距离。当1号质点向下运动到最低点，又向上运动第二次通过平衡位置时，刚好又经过\(\frac{3}{4}\)T，由于波是匀速向前传的，相当于刚才已形成的波形A又向前移动了3a距离，振动正好传到7号质点，其他的质点的位置可根据振动规律确定，把它们连接起来，得到曲线B即为题中所求波形。

 

45．一阵风吹过麦地，形成一片麦浪滚滚的景象。滚滚的麦浪是波吗？为什么？大型团体操中，人群按照口令，轮流起立蹲下形成的“人浪”是波吗？为什么？

【答案】

滚滚麦浪不是机械波，因为麦杆之间几乎没有相互联系，也难以传递振动，麦浪滚动的地方都是风吹过的地方，滚滚麦浪是风引起的。同理，人群按口令轮流起立、蹲下形成的“人浪”也不是波，人起立、蹲下是每个人自己控制的结果，不可能靠“振源”的一个人拉动成百上千的人。

 

46．判断下列说法的正误：

（1）有机械振动一定会产生机械波。（    ）

（2）有机械波一定有机械振动。（    ）

（3）只要有介质，就一定有机械波。（  ）

（4）在一个周期内，介质中的质点向前移动的距离总相等。（    ）

【答案】

（1）×（2）√（3）×（4）×

 

47．将一只闹钟放在抽成真空的玻璃罩内，闹钟的铃还能振动吗？罩外听得到声音吗？由此请你解释为何登月宇航员在月球表面只能用手势或借助无线通信来交流，而不能像在地球上那样用语言进行交流。

【答案】

能振动；听不到；月球表面没有空气，不能传递声波

 

48．一列机械波由波源传到A点然后再传到B点，则以下说法中正确的是（    ）。

（A）波由A传到B就是质点由A运动到B

（B）A质点和B质点振动频率相同

（C）A质点和B质点在任一时刻的速度相同

（D）B质点开始振动的时刻比A质点早

【答案】

B

 

49．查阅成语词典中的“随波逐流”条目，看看其中的解释是否符合物理学中相关的正确概念？

【答案】

成语词典版本很多，注释不一，但多数符合物理概念

 

50．在公园湖边的水面上往往会有漂浮的树叶等杂物，当你用细杆轻拍水面或用其他方法在水面产生一列波后，观察树叶等漂浮物是否会随波向前运动，并解释为什么？

【答案】

不会向前运动，因为波不传播质点，只传播运动和能量

 

51．把金属链条一端的小环挂在一个铁架台上，用手握住链条下端，B是阻挡物，如图所示。在手不能碰到阻挡物B的情况下，你能够使小环从铁架上脱落下来吗？请试试，如果你成功了，请说说你是怎样使小环运动的] ？

【答案】

能，用手抖动的方法在链条上产生波，使小环左右摆动

 

52．把足够长的细绳水平放置并使一端固定，在另一端产生一个开始时从平衡位置向上运动的振动。分别画出经过\(\frac{3}{2}\)T时和2T时细绳上的波形。

【答案】

 

53．一列横波沿一条长绳传播，当波源突然停止振动时（    ）。

（A）所有质点都立即停止运动

（B）已经振动的质点继续振动，尚未振动的质点不会振动

（C）离波源近的质点先停止振动，然后才是远的质点停止振动

（D）离波源远的质点先停止振动，然后才是近的质点停止振动

【答案】

C

 

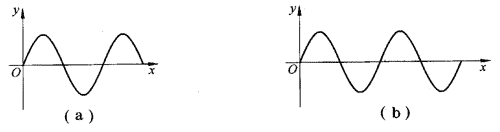
54．如图所示，呈水平状态的弹性绳，右端在竖直方向上做周期为0.4 s的振动，设t＝0时右端开始向上振动［图（a）］，则在t＝0.5s时刻绳上的波形可能是图（b）中的（    ）。

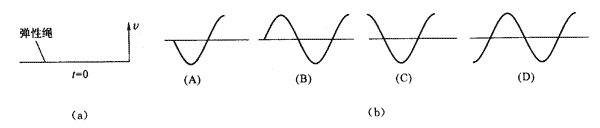
【答案】

B

 

55．如图所示，在原来静止的介质中有一列机械波沿直线传播，在此直线上A、B两点相距1.5 m，质点B完成两次全振动后质点A开始振动。求：

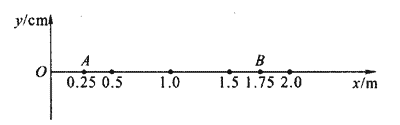
（1）波的传播方向。

（2）在图中画出，当质点A经平衡位置向下振动时。质点A、B之间的波形。（波的振幅为10 cm）

【答案】

如图所示，在原来静止的介质中有一列机械波沿直线传播，在此直线上A、B两点相距1.5 m，质点B完成两次全振动后质点A开始振动。求：

（1）波的传播方向。

（2）在图中画出，当质点A经平衡位置向下振动时。质点A、B之间的波形。（波的振幅为10 cm）

 

56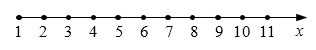．如图所示，一系列质点沿x轴排列，其间用弹性细绳连接，相邻质点间的距离都是0.2 m。t＝0时，第一个质点开始向上振动，经0.1 s，第1个质点第一次达到向上最大位移处，此时波恰好传到第3个质点。求 ：

（1）这列波的波长、波速、周期。

（2）若已知振幅为0.3 m，则求t＝0.3 s时，质点4的速度、加速度的方向；质点5、质点7的位移各为多少？

（3）画出t＝0.5 s时波的图像。

【答案】

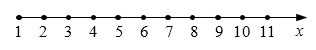如图所示，一系列质点沿x轴排列，其间用弹性细绳连接，相邻质点间的距离都是0.2 m。t＝0时，第一个质点开始向上振动，经0.1 s，第1个质点第一次达到向上最大位移处，此时波恰好传到第3个质点。求 ：

（1）这列波的波长、波速、周期。

（2）若已知振幅为0.3 m，则求t＝0.3 s时，质点4的速度、加速度的方向；质点5、质点7的位移各为多少？

（3）画出t＝0.5 s时波的图像。

 

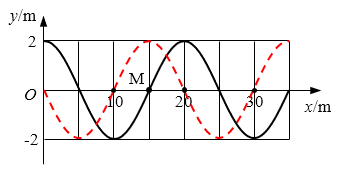
57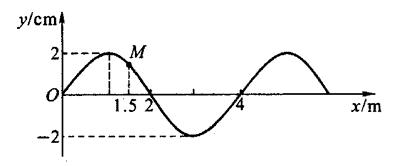．已知，t＝0时刻一列横波的图像如图所示，并已知平衡位置距原点1.5 m处的质点M正向下运动。求：

（1）波的传播方向。

（2）如波速为10 m/s，质点M第一次回到平衡位置的时间。

【答案】

（1）向左传播。

（2）0.05 s。

 

58．空气中一列声波的频率是200 Hz，它的周期是多少？如果这列声波在水中传播，它的周期是多少？如果在水中这列声波的相邻波峰或相邻波谷间的距离是7.4 m，则这列声波在水中的传播速度是多少？

【答案】

0.005 s，0.005 s，1480 m/s

 

59．图中为一列横波的图像，从图上读出波的振幅和波长。如果波速为2.0 m/s，波的频率和周期分别是多少？

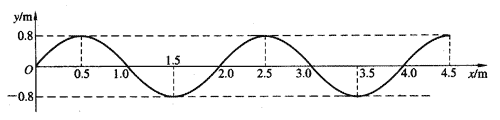
【答案】

A＝0.8 m，λ＝2 m，f＝1 Hz，T＝1 s

 

60．有一音叉的频率为440 Hz，声音在空气中传播的速度为340 m/s，音叉振动时在空气中产生的声波波长为_____m。这列声波传入声速为1500 m/s的水中后，它的频率为____Hz，波长为______m。

【答案】

0.77，440，3.4

 

61．声波在水中的传播速度是1500 m/s，水下声呐发射的频率是30000 Hz，发射后经12 s得到回声。问目标离声呐多远？水中声波的波长为多少？

【答案】

l＝9000m，A＝0.05m

 

62．摩托车发动机低速运转时，从排气管排出的废气形成空气振动的频率为40 Hz。设空气中的声速为340 m/s，则形成的声波波长为______m。若发动机转速增大，形成的声波波长将_____（选填“变大”“变小”或“不变”）。

【答案】

8.5，变小

 

63．在波的传播方向上有相距2.5 m的A、B两个质点，当A处于波峰位置时，B刚好处于波谷位置，则这列波的波长可能值为（    ）。

（A）1 m             （B）2 m             （C）2.5 m    （D）4.5 m

【答案】

A

 

64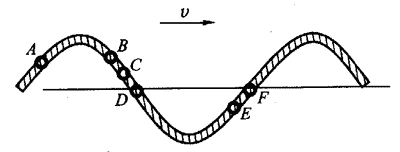．一列横波沿绳子向右传播，某时刻绳子形成如图所示的凹、凸状波形。此时对绳上A、B、C、D、E、F六个质点正确的判断是（    ）。

（A）它们的振幅不相同

（B）质点D和F的速度相同

（C）质点A和C的速度方向相同

（D）从此时算起，质点B比C先回到平衡位置

【答案】

D

 

65．第一次测定声音在水中的传播速度是1827年在日内瓦湖上用以下的方法进行的：在一只船上，实验员向水里放下一个钟，在敲击钟的同时，使船上的火药发光；在相距14 km的另一只船上，另一实验员在水里放下一个听音器，他测量从看到火药闪光到听到钟声所经过的时间为10 s。求声音在水中的传播速度。

【答案】

1400 m/s

 

66．A、B是一条水平的绳上相距为l的两点，一列横波沿绳传播，其波长为\(\frac{2}{3}\)l，当A点经过平衡位置向上运动时，B点则（    ）。

（A）经过平衡位置向上运动                   （B）经过平衡位置向下运动

（C）处于平衡位置上方位移最大处        （D）处于平衡位置下方位移最大处

【答案】

B

 

67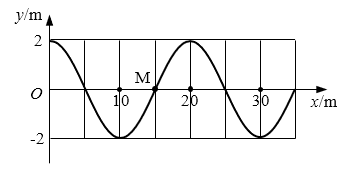．一列波在x轴上传播，波速为50 m/s，已知t＝0时刻的波形图像如图所示，图中M处的质点此时正经过平衡位置沿y轴的正方向运动。将t＝0.5 s时的波形图像用虚线画在图上（至少画出一个波长）。

【答案】

如图所示

 

68．停泊在海边的甲、乙两艘渔船，在海浪冲击下每分做100次的全振动，两船相距12 m（两船连线跟波的传播方向一致）。当甲、乙两船同时都处于海浪的波峰时，在两船之间还有一个波峰。求 ：

（1）渔船振动的周期。

（2）海浪的波长。

（3）海浪传播的速度大小。

【答案】

（1）0.6 s

（2）6 m

（3）10 m/s

 

69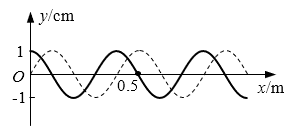．一列横波在某时刻的波形如图中实线所示，经过0.02 s后的波形如图中虚线所示，则该波的波速v不可能的是（     ）。

（A）40 m/s         （B）55 m/s

（C）35 m/s         （D）15 m/s

【答案】

A

 

70．关于周期运动，正确的判断是（    ）。

（A）匀速直线运动是周期运动        （B）匀加速直线运动是周期运动

（C）直线运动不可能是周期运动     （D）不断重复全部运动过程的运动是周期运动

【答案】

D

 

71．图中是便携式放音机的基本机械结构示意图。在放音乐时，应保持磁带盘边缘线速度不变还是保持磁带盘角速度不变？请搜索有关资料，探究正确答案 。

【答案】

为使放音乐时不失真，应保持线速度不变。实际上磁带的运动是靠匀速转动的主轴转动的。

 

72．上海和北京处在地球不同的纬度上，结合地理知识，试比较这两地的建筑物随地球自转时角速度、线速度的大小关系。

【答案】

地球上所有相对地面静止物体的角速度都相同。由于北京纬度比上海高，建筑物随地球自转的圆周半径小，所以北京建筑物随地球自转的线速度比上海小

 

73．某型号自行车的前齿轮即“牙盘”有48齿，后齿轮即“飞”有20齿，齿的大小相同，“牙盘”与“飞”用链条相连。当自行车行驶时“牙盘”与“飞”边缘上齿的线速度和角速度之比各是多少？

【答案】

线速度之比为1∶1，角速度之比为5∶12

 

74．有一个指针式的而且走时准确的钟，开始时刻时针、分针、秒针均重合在12点处。估算此后12h内，分针和秒针重合的次数、分针和时针重合的次数、秒针和时针重合的次数。

【答案】

分针和时针的重合次数为708次，分针和时针的重复次数为11次，秒针和时针的重合次数为719次

 

75．观察一辆变速自行车的变速器，说出它能变几挡速度，以及能变这几挡速度的大致原理。

【答案】

提示：变速原理是改变链条传动中大小齿轮的组合方式，主动轮与被动轮的直径比越大，获得的车速越大

 

76．物体产生振动的条件是（   ）。

（A）有方向不变、大小不变的力作用在物体上

（B）有方向不变、大小变化的力作用在物体上

（C）有方向变化、大小不变的力作用在物体上

（D）有始终指向平衡位置的力作用在物体上

【答案】

D

 

77．弹簧振子从平衡位置向最右位置的运动是（    ）。

（A）加速度不断增大的减速运动            （B）加速度不断减小的加速运动

（C）加速度不变的加速运动                   （D）加速度不断减小的减速运动

【答案】

A

 

78．某弹簧振子完成10次全振动需要5 s的时间，在此5 s的时间内通过的路程是100 cm，求此弹簧振子的振幅、周期和频率。

【答案】

A＝2.5 cm，T＝0.5 s，f＝2 Hz

 

79．第一次测定铸铁里的声速是在巴黎用下述方法进行的：在铸铁管的一端敲一下钟，在管的另一端听到两次响声，第一次是由铸铁传来的，第二次是由空气传来的，管长931 m，两次响声相隔2.5 s。如果当时空气中的声速是340 m/s，求铸铁中的声速。

【答案】

3908 m/s

 

80．如果观察者在看到闪电以后经过7 s听到雷声，试确定观察者离开闪电处的距离。

【答案】

2380 m

 

81．蝙蝠能发射超声波，但它的发射是间歇性的。若它每秒共发射50次，每次发出100个频率为1×10⁵ Hz的超声波波形，它在2 s内累计有多少时间在发射超声波？

【答案】

0.1 s

 

82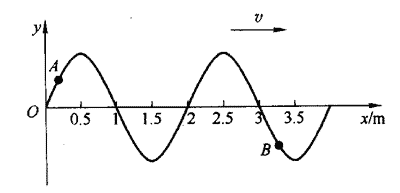．图中表示某一时刻的波形图，已知波速为0.5 m/s，波沿着x轴的正方向传播，

（1）在图示时刻，质点A和B向什么方向运动 ？

（2）分别画出经过1 s后和经过4 s后的波形曲线。

【答案】

（1）A竖直向下，B竖直向上

（2）略