1．一杯水含有大量的水分子，若杯中水的温度升高，则（      ）

（A）水分子的平均动能增大            （B）只有个别水分子动能增大

（C）所有水分子的动能都增大        （D）每个水分子的动能改变量均相同

【答案】

A

 

2．在一密闭的钢瓶内有一定质量的气体，能反映钢瓶内气体等容变化过程的是图（     ）

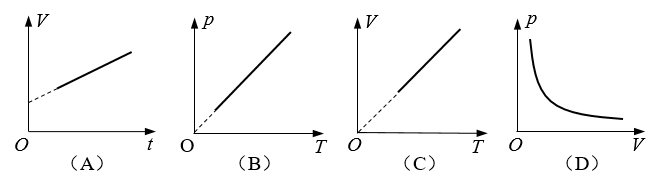
【答案】

B

 

3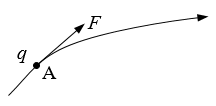．如图，一电荷量为q的正点电荷位于电场中A点，受到的电场力为F，则A点的电场强度大小E＝\(\frac{F}{q}\)，方向与F相同。若把该点电荷换为电荷量为2q的负点电荷，则A点的电场强度（     ）

（A）大小仍为E，方向与原来相反         （B）大小仍为E，方向与原来相同

（C）大小变为E/2，方向与原来相反      （D）大小变为E/2，方向与原来相同

【答案】

B

 

4．设地球半径为R，一卫星在地面上受到地球的万有引力为F，则该卫星在半径为3R的轨道上绕地球运行时，受到地球的万有引力为（     ）

（A）F/9              （B）F/4              （C）F/3              （D）F/2

【答案】

A

 

5．右图为一门电路的两个输入端A、B与输出端Z的电压信号图，由此可推断该门电路是（     ）

（A）“与”门             （B）“或”门

（C）“非”门              （D）“与非”门

 

【答案】

B

 

6．卢瑟福利用α粒子轰击金箔的实验研究原子结构，得到的实验结果有（     ）

（A）所有α粒子几乎无偏转地穿过金箔

（B）大多数α粒子发生较大角度的偏转

（C）向各个方向运动的α粒子数目基本相等

（D）极少数α粒子产生超过90°的大角度偏转

【答案】

D

 

7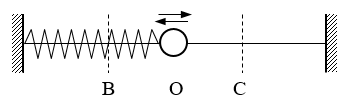．如图，O点为弹簧振子的平衡位置，小球在B、C间做无摩擦的往复运动。在小球运动到O的过程中，小球的（     ）

（A）速度不断增大，加速度不断增大

（B）速度不断减小，加速度不断增大

（C）速度不断增大，加速度不断减小

（D）速度不断减小，加速度不断减小

【答案】

C

 

8．地球绕太阳和月球绕地球的运动均可看作匀速圆周运动。地球绕太阳每秒运动29.79km，一年转一圈；月球绕地球每秒运动1.02km，28天转一圈。设地球的线速度为v₁，角速度为ω₁；月球的线速度为v₂，角速度为ω₂，则（      ）

（A）v₁＞v₂，ω₁＞ω₂                （B）v₁＜v₂，ω₁＞ω₂

（C）v₁＞v₂，ω₁＜ω₂                （D）v₁＜v₂，ω₁＜ω₂

【答案】

C

 

9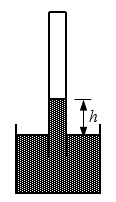．如图，开口向下的玻璃管插入水银槽中，管内封闭了一段气体，气体压强为p，管内外水银面高度差为h。若大气压强增大，则（     ）

（A）p增大，h增大          （B）p减小，h增大

（C）p增大，h减小          （D）p减小，h减小

 

【答案】

 A

 

10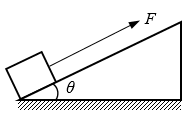．如图，斜面的倾角为θ，用平行于斜面的恒力F拉质量为m的物体，使它沿斜面上升的高度为h。在此过程中，该恒力对物体所做的功是（      ）

（A）Fh （B）mgh      （C）Fhsinθ  （D）Fh/sinθ

 

【答案】

D

 

11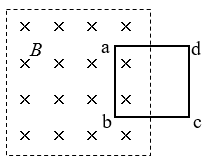．如图，正方形线圈abcd的一半处于匀强磁场中，线圈平面与磁场方向垂直。在线圈以ab为轴旋转90°的过程中，穿过线圈的磁通量大小（    ）

（A）一直减小                   （B）先增大后减小

（C）先减小后增大            （D）先不变后减小

【答案】

D

 

12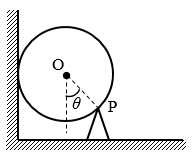．如图，一个质量为m的均匀光滑小球处于静止状态，三角劈与小球的接触点为P，小球重心为O，PO连线与竖直方向的夹角为θ。则三角劈对小球的弹力（    ）

（A）方向竖直向上，大小为mg

（B）方向竖直向上，大小为mgcosθ

（C）方向沿OP向上，大小为mg/cosθ

（D）方向沿OP向上，大小为mgtanθ

【答案】

C

 

13．甲、乙两小车在t＝0时从同一地点朝相同方向做直线运动，右图为两小车运动的v-t图像。由此可知，甲做________运动，当两小车速度相等时，它们相距_____m。

【答案】

匀速直线（或匀速），1

 

14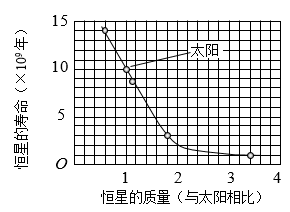．右图为恒星的寿命与其质量的关系图。由图可知，恒星质量越大，其寿命越________（选填“长”或“短”），若一恒星的质量为太阳质量的1.8倍，则它的寿命约为________×10⁹年。

 

【答案】

短，3

 

15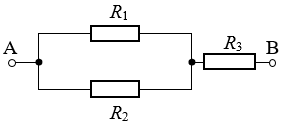．在图示电路中，三个电阻的阻值分别为R₁＝2Ω、R₂＝6Ω和R₃＝5Ω，A、B间的总电阻大小为_______Ω。若在A、B间加一恒定电压，则通过R₁和R₃的电流之比为_________。

【答案】

6.5，3∶4

 

16．右图为一列沿x轴正方向传播的横波在某时刻的波形图，波的振幅为____________m，此时，在x＝2.5m处质点的运动方向___________（选填“向上”、“向下”或“向右”）。

 

【答案】

 0.1，向下

 

17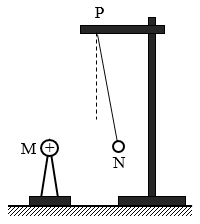．如图，用绝缘丝线将一带正电的小球N挂在水平横杆上的P点，在N的左侧放置一带正电的小球M，由于静电相互作用，N平衡时丝线与竖直方向有一定的偏角。如果M的电荷量加倍，丝线偏角________（选填“变大”、“变小”或“不变”）。如果两球的电荷量不变，把M向左移动一定距离，N静止时受到的静电力________（选填“变大”、“变小”或“不变”）。

 

【答案】

变大，变小

 

18．右表为某品牌微波炉的技术参数，根据相关数据可知该微波炉所用微波的波长为_______m（保留两位小数）。若微波炉工作电流为额定电流，加热食品120s，消耗的电能为________J。（注：1MHz＝1×10⁶Hz）

额定电压/额定电流	220V/5A
微波频率/输出功率	2450MHz/700W
内腔容积	20L

【答案】

0.12，1.32×10⁵

 

19．如图，木块以某初速度冲上一光滑斜面，画出木块在斜面上的受力示意图。

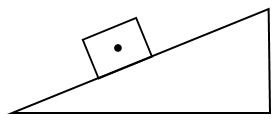
【答案】

 

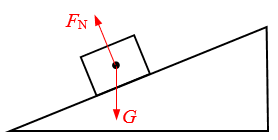
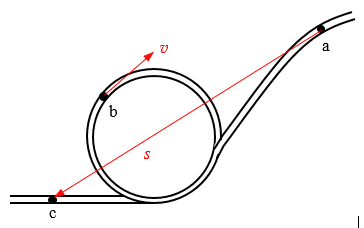
19．过山车沿着图示曲线轨道从a点滑下，沿圆轨道运动一圈后，从c点滑出，画出：①过山车从a点运动到c点的位移；②过山车在b点时的速度方向。

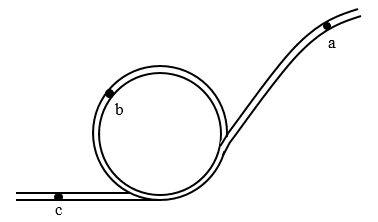
【答案】

 

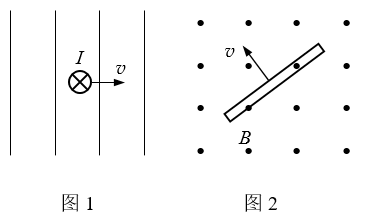
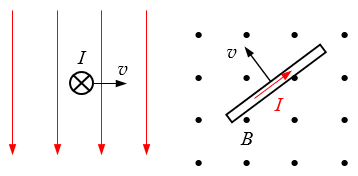
19．闭合回路的一段导线以速度v垂直磁场做切割磁感线运动。

①根据图1中导线的运动方向与感应电流方向画出磁场方向；

②根据图2中导线的运动方向与磁场方向，画出感应电流方向。

【答案】

 

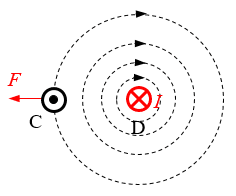
19．如图，C、D为两根垂直于纸面的平行通电直导线，C的电流方向垂直纸面向外，D周围的同心圆表示D中电流的磁场分布。画出：①导线D中的电流方向；②导线C受到的磁场力方向。

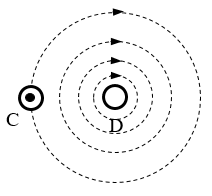
【答案】

 

20．图1为“用DIS研究物体的加速度与力的关系”的实验装置图，A为带有位移传感器的小车，B为若干规格相同的回形针。实验中，用回形针的重力大小代替小车所受拉力大小，摩擦阻力不计。

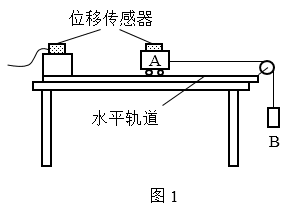
（1）为了研究物体的加速度与力的关系，实验中应保持___________不变。

回形针个数N	4	8	12	16	20
小车加速度a/m·s-2	0.10	0.20	0.30	0.40	0.50

（2）改变回形针的个数N，测得相应的加速度a，数据见右表。

①根据表中数据，在图2中画出小车加速度a与回形针个数N的关系图线。

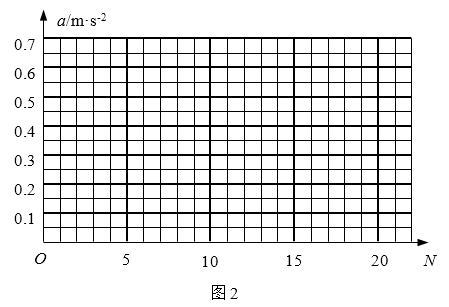
②由a-N的关系图线，写出a与N的定量关系式：______________________。

③设一个回形针的重力为G，写出小车加速度a与它所受拉力F的定量关系式：______________________。

【答案】

（1）小车（与位移传感器的）总质量

（2）①

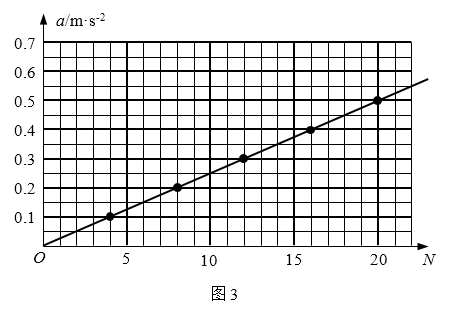
②a＝\(\frac{1}{{40}}\)N

③a＝\(\frac{F}{{40G}}\)

【解析】

（1）当研究物体的加速度与力的关系时，应保持小车A（包括固定在其上的位移传感器）总质量不变，这体现了控制变量法的实验思想。

（2）根据方格纸内给定的标度，所测量出的每组数据都能在其中找到对应的点，将这些数据点用平滑直线连起来就得到a-N的关系图形，如图3所示。因为这个图线为一条过原点的直线，故不难写出它的方程为：a＝\(\frac{1}{{40}}\)N，这就是a与N的定量关系式。因实验中用回形针的重力大小替代小车所受拉力F的大小，故F＝NG，带入a＝\(\frac{1}{{40}}\)N可得a＝\(\frac{F}{{40G}}\)。

 

21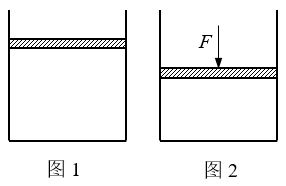．如图1，在开口向上的气缸内，一个质量不计的活塞封闭了一定质量的气体，活塞截面积S＝5.0×10^－4m²，气体体积V₁＝6.0×´10^－5m³。如图2，在活塞上施加一压力，缓慢压缩气体，压缩过程中气体温度不变。当压力F＝10N时，求：

（1）气缸内气体压强p₂；

（2）气缸内气体体积V₂。（大气压强p₀＝1.0×10⁵Pa，不计活塞和气缸间的摩擦）

【答案】

（1）p₂＝1.2×10⁵Pa，

（2）V₂＝5.0×10^－5m³

【解析】

（1）气体对活塞的压力与力F及大气对活塞的压力平衡，则气体的压强为

F＋p₀S＝p₂S

p₂＝p₀＋\(\frac{F}{S}\)

＝（1.0×10⁵＋\(\frac{{10}}{{5.0 \times {{10}^{ - 4}}}}\)）Pa

＝1.2×10⁵Pa，

（2）初态时，p₁＝p₀，由波意耳定律p₁V₁＝p₂V₂

V₂＝\(\frac{{{p_0}{V_1}}}{{{p_2}}}\)＝\(\frac{{1.0 \times {{10}^5} \times 6.0 \times {{10}^{{\rm{ - }}5}}}}{{1.2 \times {{10}^5}}}\)m³＝5.0×10^－5m³

 

22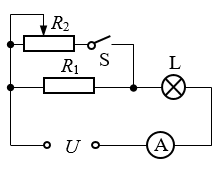．在图示电路中，稳压电源的电压U＝9V，电阻R₁＝9Ω，R₂为滑动变阻器，电流表为理想电表。小灯泡L标有“6V，6W”字样，电阻随温度变化不计。电键S断开时，求：

（1）电流表的示数I；

（2）小灯泡L的实际功率P_L；

（3）闭合电键S，为使小灯泡L正常发光，滑动变阻器R ₂接入电路的电阻值是多少？

 

【答案】

（1）I＝0.6A，

（2）P_L＝2.16W

（3）R₂＝4.5Ω

【解析】

（1）小灯泡的电阻R_L＝\(\frac{{U_L^2}}{{{P_L}}}\)＝\(\frac{{{6^2}}}{6}\)Ω＝6Ω

电键S断开时，小灯泡和R₁串联，电流表的示数

I＝\(\frac{U}{{{R_1} + {R_L}}}\)＝\(\frac{9}{{9 + 6}}\)A＝0.6A，

（2）电键断开时灯泡L的实际功率

P_L＝I²R_L＝0.6²×6W＝2.16W

（3）当电键S闭合时，R₁与R₂并联后与小灯泡串联，小灯泡正常发光时两端电压U_L为6V，通过灯泡的电流

I_L额＝\(\frac{{{P_L}}}{{{U_L}}}\)＝1A

R₂两端的电压U₂＝U－U_L额＝（9－6）V＝3V

通过R₂的电流I₂＝I_L额－I₁＝I_L额－\(\frac{{{U_2}}}{{{R_1}}}\)＝\(\frac{2}{3}\)A

R₂＝\(\frac{{{U_2}}}{{{I_2}}}\)＝4.5Ω

 

23．如图，AB为粗糙的长直轨道，与水平方向的夹角为37°，BCD为光滑曲线轨道，两段轨道在B处光滑连接。B、C、D三点离水平地面的高度分别为h₁＝0.50m，h₂＝1.75m和h₃＝1.50m。一质量m＝0.20kg的小环套在轨道AB上，由静止开始释放，经过t＝1.2s到达B点，速度v_B＝6.0m/s。求：（sin37°＝0.6，cos37°＝0.8，g取10m/s²）

（1）小环沿AB运动的加速度a的大小；

（2）小环沿AB运动时所受摩擦力F_f的大小；

（3）小环离开轨道D处时的速度v_D的大小；

（4）若使小环以最小速度落地，求小环在AB上释放处离地的高度h。

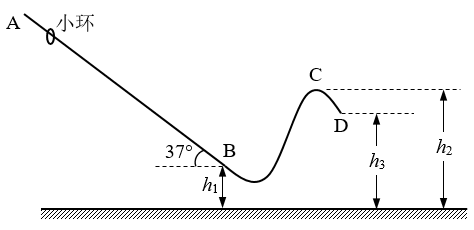
【答案】

（1）a＝5m/s²

（2）F_f＝0.2N，

（3）v_D＝4m/s

（4）h＝2m

【解析】

（1）小环在AB上做匀加速直线运动

a＝\(\frac{{{v_B}}}{t}\)＝5m/s²

（2）小环在AB上受重力、支持力和摩擦力，由牛顿第二定律：

mgsin37°－F_f＝ma

F_f＝mgsin37°－ma＝（0.20×10×0.6－0.20×5）N＝0.2N，

（3）小球由B运动到D，机械能守恒

mgh₁＋\(\frac{1}{2}\)mv_B²＝mgh₃＋\(\frac{1}{2}\)mv_D²

可求得v_D＝4m/s，

（4）小环运动到C点v_C＝0，落地速度最小，

B运动到C，机械能守恒

mgh₁＋\(\frac{1}{2}\)mv_Bʹ²＝mgh₂

可求得v_Bʹ＝5m/s

小环从释放运动到B的位移

s＝\(\frac{{{v_B}{{^\prime }^2}}}{{2a}}\)＝2.5m

小环释放处离地面的高度

h＝h₁＋ssin37°＝（0.5＋2.5×0.6）m＝2m