1．对于任何一个质量不变的物体，下列说法中正确的是（    ）

（A）物体的动量发生变化，其速率一定变化

（B）物体的动量发生变化，其速率不一定变化

（C）物体的速率发生变化，其动量一定变化

（D）物体的速率发生变化，其动量不一定变化

【答案】

BC

 

2．两个物体在光滑水平面上相向运动，在正碰以后都停下来，那么这两个物体在碰撞以前（    ）

（A）质量一定相等                          （B）速度大小一定相等

（C）动量大小一定相等                   （D）动能一定相等

【答案】

C

 

3．质量为m的钢球自高处落下，以速率v₁碰地，竖直向上弹回，碰撞时间极短，离地的速率为v₂。在碰撞过程中，地面对钢球的冲量的方向和大小为（    ）

（A）向下，m（v₁－v₂）                         （B）向下，m（v₁+v₂）

（C）向上，m（v₁－v₂）                         （D）向上，m（v₁+v₂）

【答案】

D

 

4．物体在恒力作用下作直线运动，在t₁时间内物体的速度由零增大到v，F对物体做功W₁，给物体冲量I₁。若在t₂时间内物体的速度由v增大到2v，F对物体做功W₂，给物体冲量I₂，则（    ）

（A）W₁=W₂，I₁=I₂                       （B）W₁=W₂，I₁＞I₂

（C）W₁<W₂，I₁=I₂                        （D）W₁>W₂，I₁=I₂

【答案】

C

 

5．如图所示，质量为m的小球在水平面内作匀速圆周运动，细线长L，偏角θ，线的拉力为F，小球作圆周运动的角速度为ω，周期为T，在T/2时间内质点所受合力的冲量为（    ）

（A）(F－mgcosθ)\(\frac{T}{2}\)          （B）Fsinθ×\(\frac{T}{2}\)

（C）2mωθLsinθ                 （D）2mωL

【答案】

C

【解析】

由于合外力是变力，不能直接求其冲量，但可以根据动量定理求其动量的变化量

 

6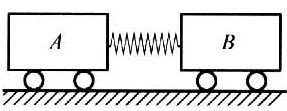．原来静止的两小车，用一条被压缩的轻质弹簧连接，如图所示。如果A车的质量为m_A=2 kg，B车的质量为A车的2倍，弹簧弹开的时间为0.1 s，弹开后B车的速度为v_B=1 m/s，则B车所受的平均作用力是（    ）

（A）0.4 N           （B）40 N            （C）4 N              （D）20 N

【答案】

B

【解析】

先对A、B组成的系统运用动量守恒定律，然后对B车运用动量定理求出其作用力

 

7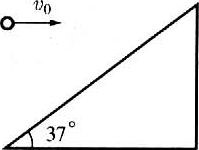．如图所示，质量为50 g的小球以12 m/s的水平速度抛出，恰好与斜面垂直碰撞，其碰撞后的速度的大小恰好等于小球抛出时速度的一半。小球与斜面碰撞过程中所受到的冲量的大小是（    ）。

（A）1.4 N·s        （B）0.7 N·s         （C）1.3 N·s         （D）1.05 N·s

【答案】

C

【解析】

先根据平抛运动的知识求得小球与斜面碰撞前的速度，再结合动量定理求解

 

8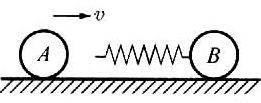．如图所示，在光滑的水平面上放有两个小球A和B，其质量m_A＜m_B，B球上固定一轻质弹簧。若将A球以速率v去碰撞静止的B球，下列说法中正确的是（    ）。

（A）当弹簧压缩量最大时，两球速率都最小

（B）当弹簧恢复原长时，B球速率最大

（C）当A球速率为零时，B球速率最大

（D）当B球速率最大时，弹性势能不为零

【答案】

B

【解析】

A、B小球组成的系统动量守恒，同时两球的动能和弹簧的弹性势能之和保持不变

 

9．水平拉力F₁、F₂分别作用在水平面上的物体上一段时间后撤去，使物体都由静止开始运动而后又停下。如物体在这两种情况下的总位移相等，且F₁＞F₂，那么在这样的过程中（    ）。

（A）F₁比F₂的冲量大             （B）F₁比F₂的冲量小

（C）F₁与F₂的冲量相等          （D）F₁与F₂的冲量大小无法比较

【答案】

B

【解析】

可以结合全过程的v-t图像来帮助求解，在图像中，外力撤去后物体的加速度相同

 

10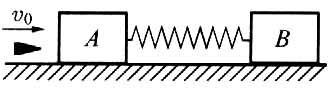．如图所示，一轻质弹簧两端连着物体A，B，放在光滑的水平面上，若物体A被水平速度为v₀的子弹射中，且后者嵌在物体A的中心，已知物体A的质量是物体B质量的3/4，子弹质量是物体B的1/4，弹簧被压缩到最短时，求物体A、B的速度。

【答案】

v′=\(\frac{1}{8}\)v₀

 

11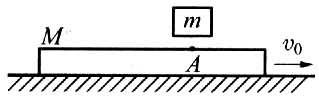．如图所示，在光滑的水平面上有一质量为M的长条木板，以速度v₀向右作匀速直线运动，将质量为m的小铁块轻轻放在小板上的A点（这时小铁块相对地面速度为零），小铁块相对木板向左滑动。由于小铁块和木板间有摩擦，最后它们之间相对静止，已知它们之间的动摩擦因数为μ，问：

（1）小铁块跟木板相对静止时，它们的共同速度多大？

（2）它们相对静止时，小铁块与A点距离多远？

（3）在全过程中有多少机械能转化为热能？

【答案】

（1）vʹ=\(\frac{{M{v_0}}}{{M + m}}\)

（2）L_相=\(\frac{{Mv_0^2}}{{2\mu g(M + m)}}\)

（3）Q=\(\frac{{Mmv_0^2}}{{2(M + m)}}\)

 

12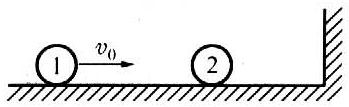．如图所示，光滑水平面上有两个质量分别为m₁和m₂的小球1和2，它们在一条与右侧竖直墙壁垂直的直线上前后放置。设开始时球2静止，球1以速度v₀对准球2运动，不计各种摩擦，所有碰撞都是弹性的，如果要求两球只发生两次碰撞，试确定m₁/m₂比值的范围。

【答案】

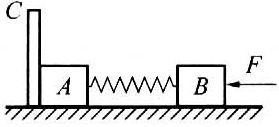
\(\frac{1}{3}\)＜m₁/m₂＜1+\(\frac{{2\sqrt 5 }}{5}\)

 

13．下列关于动量的论述中正确的是（    ）。

（A）质量大的物体动量一定大                      （B）速度大的物体动量一定大

（C）两物体动能相等，动量大小一定相等     （D）两物体动能相等，动量一定相等

【答案】

C

 

14．关于物体的动量和动能，下列说法中正确的是（    ）。

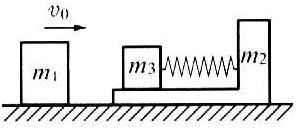
（A）一物体的动量不变，其动能一定不变

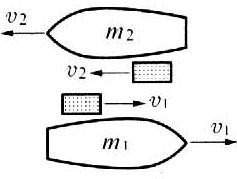
（B）一物体的动能不变，其动量一定不变

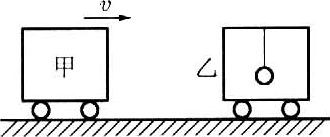
（C）两物体的动量相等，其动能一定相等

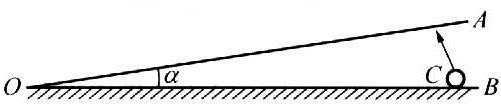
（D）两物体的动能相等，其动量一定相等

【答案】

A

 

15．两个具有相等动量的物体A、B，质量分别为m_A和m_B，且m_A＞m_B，比较它们的动能，则（    ）。

（A）B的动能较大            （B）A的动能较大

（C）动能相等                   （D）不能确定

【答案】

A

 

16．放在水平桌面上的物体质量为m，用一个水平推力F推它，作用时间为t，物体始终不动，那么在t时间内，推力对物体的冲量应为______。

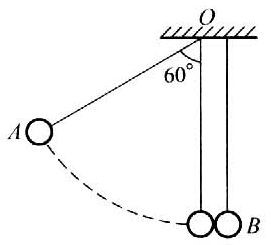
【答案】

Ft

 

17．甲、乙两物体的质量之比为 m_甲∶m_乙 = 1∶4，若它们在运动过程中的动能相等，则它们动量大小之比 p_甲：p_乙 是（    ）。

（A）1∶1            （B）1∶2            （C）1∶4            （D）2∶1

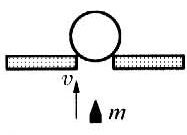
【答案】

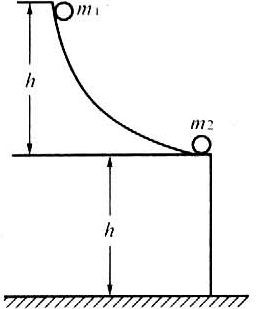
B

 

18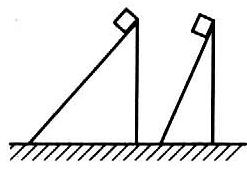．如图所示，两个质量相等的物体在同一高度沿倾角不同的两个光滑斜面由静止自由滑下，到达斜面底端的过程中，两个物体具有的相同的物理量是（    ）。

（A）重力的冲量                                    （B）弹力的冲量

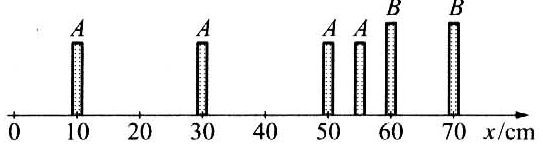
（C）合力的冲量                                    （D）刚达到底端时的动量

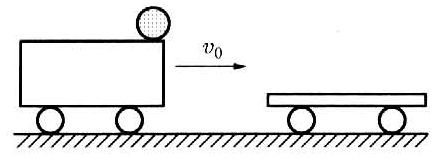
（E）刚达到底端时动量的水平分量        （F）以上几个量都不对

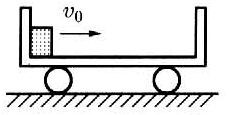
【答案】

F

 

19．质量为2 kg的物体作竖直上抛运动，4 s后回到出发点，不计空气阻力，在此过程中物体动量的改变和所受的冲量分别为（g取10 m/s²）（    ）。

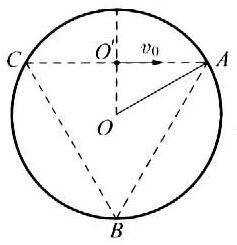
（A）80 kg·m/s和80 N·s，方向均为竖直向下

（B）80 kg·m/s，方向竖直向上，80 N·s，方向竖直向下

（C）40 kg·m/s和40 N·s，方向均为竖直向下

（D）80 kg·m/s和40 N·s，方向均为竖直向下

【答案】

A

 

20．质量不等的两个物体静止在光滑的水平面上，两物体在外力作用下获得相同的动能，则下列说法中正确的是（    ）。

（A）质量大的物体动量变化小               （B）质量大的物体受到的冲量大

（C）质量大的物体末动量小                   （D）质量大的物体动量变化率一定大

【答案】

B

 

21．以初速度v₀=40 m/s竖直向上抛出一质量为4 kg物体。则第2秒末的动量为____kg·m/s，第5秒末动量为____kg·m/s，从第2秒末到第5秒末动量的变化量为____kg·m/s（g取10 m/s²）。

【答案】

80，－40，－120

 

22．从水平地面上方同一高度处，使a球竖直上抛，使b球平抛，且两球质量相等，初速度大小相同，最后落于同一水平地面上（空气阻力不计）。下列说法中正确的是（    ）。

（A）两球着地时的动量相同            （B）两球着地时的动能相同

（C）重力对两球的冲量相同            （D）重力对两球所做的功相同

【答案】

BD

 

22．要计算竖直上抛一个物体的过程中，手对抛出物作用力的冲量，如不计空气阻力，所需的已知条件为下列几种组合中的（    ）。

（A）物体的质量m，它能上升的最大高度H

（B）抛出时的初速v₀，它能上升的最大高度H

（C）抛出时用力F的大小，物体上升到最高处所需的时间t

（D）物体的重力G，它在空中的时间t′

【答案】

AD

 

24．用绳子拴一个质量是0.1 kg的小球，由静止开始以2 m/s²的加速度竖直向上运动，头3 s内绳子拉力对物体的冲量的大小为______N·s；头3 s内物体动量变化的大小为_____kg·m/s（g值取10 m/s²）。

【答案】

3.6，0.6

 

25．质量为0.4 kg的小球以10 m/s的速度从5 m高的平台边缘水平抛出，小球落地时动量的大小是______kg·m/s，方向是____________，小球运动全过程中动量的变化是_____kg·m/s（g取10 m/s²）。

【答案】

4，与水平方向夹角45°，4

 

27．如果某物体作匀速圆周运动的动量大小为p，经过一段时间后其速度方向改变了θ角，它的动量变化的大小为______。

【答案】

2psin\(\frac{\theta }{2}\)

 

27．甲、乙两物体质量相等，并排静止在光滑的水平面上。现用一水平恒力F推动甲物体，同时在与F力相同方向上给物体乙一个瞬间冲量I，使两物体开始运动。当两物体重新相遇时，经历的时间t=______。

【答案】

\(\frac{{2I}}{F}\)

 

28．质量为1.5 kg的物体，以4 m/s的初速度竖直上抛，不计空气阻力。求物体抛出时和落回抛出点时的动量及这段时间内动量的变化量和重力的冲量（g取10 m/s²）。

【答案】

6 kg·m/s，方向竖直向上；6 kg·m/s，方向竖直向下；12 kg·m/s，方向竖直向下；12 N·s，方向竖直向下

 

29．以初速度v₀=10 m/s水平抛出一个质量为1 kg的物体，若在抛出3 s后它末与地面及其它物体相碰，求它在3 s内重力的冲量，3 s内物体动量的变化量，第3秒末的动量（g取10 m/s²）。

【答案】

I=Ft=mgt=30N·s，Δp=30kg·m/s，p_末=mv_末=1×10kg·m/s=10kg·m/s

 

30．如图所示，物体质量m=2 kg，放在光滑水平桌面上，在恒定的牵引力F作用下由位置A运动到位置B，速度由2 m/s增加到4 m/s，力F与水平面成60°角，求在此过程中力F的冲量。

【答案】

8 N·s

 

31．一个质量为m的小球，从高度为H的地方自由落下，与水平地面碰撞后向上弹起，设碰撞时间为定值t，则在碰撞过程中，下列关于小球对地面的平均冲击力与球弹起的高度h的关系中正确的是（设冲击力远大于重力）（    ）。

（A）h越大，平均冲击力越大

（B）h越小，平均冲击力越大

（C）平均冲击力大小与h无关

（D）若h一定，平均冲击力与小球质量成正比

【答案】

AD

 

32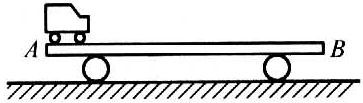．如图所示，质量为4 kg的平板车静止在光滑水平面上，一质量为1 kg的玩具小车在1 s内由静止从车的左端A点加速运动到车的右端B点，AB间距0.2 m，在这段时间内小车对平板车的水平冲量大小为多少？

【答案】

0.32 N·s

 

33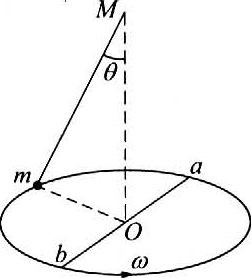．如图所示，绳子一端固定于M点，另一端系一质量为m的质点以角速度ω绕竖直轴作匀速圆周运动，绳子与竖直轴之间的夹角为θ。已知a、b为直径上的两点，求质点从a点运动到b点绳子张力的冲量的大小。

【答案】

\(\frac{{mg}}{\omega }\sqrt {{\pi ^2} + 4{{\tan }^2}\theta } \)

 

34．在一条直线上运动的物体，其初动量为8 kg·m/s，它在第1秒内受到的冲量为－3 N·s，第2秒内受到的冲量为5 N·s，它在第2秒末的动量为（    ）。

（A）10 kg·m/s           （B）11 kg·m/s            （C）13 kg·m/s            （D）16 kg·m/s

【答案】

A

 

35．某物体在运动过程中，受到的冲量为－1 N·s，则（    ）。

（A）物体原动量方向一定与这个冲量方向相反

（B）物体的末动量一定是负值

（C）物体的动量一定要减少

（D）物体动量的增量一定与所规定的正方向相反

【答案】

D

 

36．人从高处跳到低处时，为了安全，一般都让脚尖先着地，这样做是为了（    ）。

（A）减小冲量

（B）减小动量的变化量

（C）增大与地面的作用时间，从而减小冲力

（D）增大人对地面的压强，起到安全作用

【答案】

C

 

37．物体在恒定合外力作用下运动，则（    ）。

（A）物体一定作直线运动

（B）物体的动量变化率一定恒定

（C）物体的动量增量与时间成正比

（D）单位时间内物体动量的增量与物体的质量无关

【答案】

BCD

 

38．玻璃杯从同一高度落下，掉在石头上比掉在草地上容易碎，这是由于玻璃杯在与石头的撞击过程中（    ）。

（A）玻璃杯的动量较大                   （B）玻璃杯受到的冲量较大

（C）玻璃杯的动量变化较大            （D）玻璃杯的动量变化较快

【答案】

D

 

39．质量为1.0 kg的小球从20 m处自由下落到软垫上，弹后上升的最大高度为5.0 m，小球与软垫接触的时间为1.0 s，接触时间内小球受到合力的冲量大小为（空气阻力）不计，g取10 m/s²）（     ）。

（A）10 N·s                （B）20 N·s                （C）30 N·s                （D）40 N·s

【答案】

D

 

40．以15 m/s的速度平抛一个小球，小球的质量为1 kg，经2 s小球落地，不计空气阻力，g取10 m/s²。小球落地时的速度大小为_____m/s。在这一过程中，小球的动量变化的大小为_____kg·m/s 。

【答案】

25，20

 

41．小球的质量为2m，以速度v沿水平方向垂直撞击墙壁，球被反方向弹回速度大小是\(\frac{4}{5}\)v，球与墙撞击时间t，那么在撞击过程中，球对墙的平均冲力大小是（    ）。

（A）\(\frac{{2mv}}{{5t}}\)                  （B）\(\frac{{8mv}}{{5t}}\)                  （C）\(\frac{{18mv}}{{5t}}\)          （D）\(\frac{{2mv}}{{t}}\)

【答案】

C

 

42．质量为m的物体，以初速度v₀竖直上抛，然后又回到原抛出点。若不计空气阻力，物体所受的总冲量和平均冲力分别是（以竖直向上方正方向）（    ）。

（A）－mv₀，\(\frac{1}{2}\)mg      （B）－2mv₀，－mg    （C）－2mv₀，mg        （D）2mv₀，－mg

【答案】

B

 

43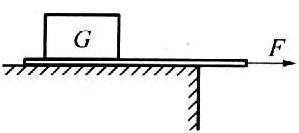．如图所示，把重物G压在纸带上，若用一水平力迅速拉动纸带，纸带将会从重物下抽出；若缓慢拉动纸带，纸带也从重物下抽出，但重物跟着纸带一起运动一段距离。下列解释上述现象的说法中正确的是（    ）。

（A）在缓慢拉动纸带时，纸带给重物的摩擦力大

（B）在迅速拉动纸带时，纸带给重物的摩擦力小

（C）在缓慢拉动纸带时，纸带给重物的冲量大

（D）在迅速拉动纸带时，纸带给重物的冲量小

【答案】

CD

 

44．竖直上抛某物体，物体达到最高点后又回到抛出点，设物体所受空气阻力大小不变，则（    ）。

（A）上升过程中重力的冲量比下落过程中重力的冲量小

（B）全过程中物体的动量增量方向向下

（C）空气阻力的冲量值上升与下落过程相等

（D）空气阻力在全过程中的合冲量方向向上

【答案】

ABD

 

45．水力采煤是利用高速水流冲击煤层而进行的。假如煤层受到3.6×10⁶ N/m²的压强冲击即可被破碎，若高速水流沿水平方向冲击煤层，不考虑水的反向溅射作用，则冲击煤层的水流速度至少应为（    ）。

（A）30 m/s         （B）40 m/s         （C）45 m/s         （D）60 m/s

【答案】

D

 

46．一质量为100 g的小球从0.80 m高处自由下落到一厚软垫上。若以小球接触软垫到小球陷到最低点经历了0.20 s，则这段时间内软垫对小球的冲量为_____N·s（g取10 m/s²，不计空气阻力）。

【答案】

0.6

 

47．跳伞员从飞机上跳下，经过一段时间速度增大到收尾速度50 m/s时才张开伞，这时，跳伞员受到很大的冲力。设张伞时间经1.5 s，伞开后跳伞员速度为5 m/s，速度方向始终竖直向下，则冲力为体重的_____倍。

【答案】

4

 

48．质量为50 g的机枪子弹的出膛速度为1000 m/s，假设机枪每分钟发射120发子弹，则在射击时机枪手需用多大的力抵住机枪？

【答案】

100 N

 

49．质量为0.2 kg的球，从5.0 m高处自由下落到水平钢板上又被竖直弹起，弹起后能达到的最大高度为4.05 m，如果球从开始下落到弹起达到最大高度所用时间为1.95 s，不考虑空气阻力（g取10 m/s²），求小球对钢板的作用力。

【答案】

78 N

 

50．两个质量不同的物体，以相同的初动量开始沿同一水平面滑动，设它们与水平面间的动摩擦因数相同，则它们滑行的距离大小关系是（    ）。

（A）质量大的物体滑行距离较大

（B）质量小的物体滑行距离较大

（C）两物体滑行距离一样大

（D）条件不足，无法比较

【答案】

B

 

51．枪筒长为L，子弹质量为m，设子弹被击发后在枪筒内作匀加速直线运动，运动的时间为t，则（    ）。

（A）子弹离开枪口时的动能为\(\frac{{m{L^2}}}{{2{t^2}}}\)

（B）子弹在枪筒内运动过程中外力的冲量为\(\frac{{m{L^2}}}{{{t^2}}}\)

（C）子弹在枪筒内运动过程中，合外力对它做的功是\(\frac{{2m{L^2}}}{{{t^2}}}\)

（D）子弹受到的平均冲力是\(\frac{{2m{L^2}}}{{{t^2}}}\)

【答案】

C

 

51．在光滑的水平面上，质量为M的平板小车以速度v₀作匀速直线运动。质量为m的物体竖直掉在车上。由于物体和车之间的摩擦，经时间t后它们以共同的速度前进，在这个过程中，小车所受摩擦力的大小为_____。

【答案】

\(\frac{{mM{v_0}}}{{(M + m)t}}\)

 

53．以2 m/s的速度作水平匀速运动的质量为0.1 kg的物体，从某一时刻起受到一个始终与速度方向垂直、大小为2 N的力的作用，在作用0.1π（s）后，物体的速度大小是_______m/s，这0.1π（s）内，力对物体的冲量大小为______N·s。

【答案】

2，0.4

 

54．有一质量为50 g的小球，以10 m/s的速度垂直射到竖直的墙壁上又被垂直墙壁反弹，落到离墙5 m远的水平地面上。若已知小球击墙点离地高5 m，球与墙作用时间为0.05 s，求小球与墙撞时墙对球的平均作用力。

【答案】

15 N

 

55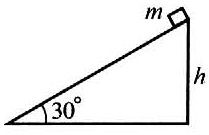．光滑斜面高h=0.8 m，质量m=1 kg的滑块从固定的斜面顶端由静止释放，如图所示。滑块滑到底端的过程中（g取10 m/s²）：

（1）中力对滑块所做的功为_____J；

（2）滑块的动能增量为_____J；

（3）重力对滑块的冲量为______N·s；

（4）滑块的动量增量为_____kg·m/s。

【答案】

（1）8

（2）8

（3）8

（4）4

 

56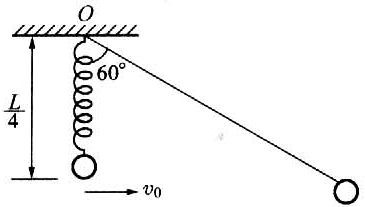．如图所示，长为L的轻绳一端系于固定点O，另一端系一质量为m的小球，将小球从O点正下方L/4处，以水平初速度向右抛出，经一定时间绳被拉直，以后小球将以O为支点在竖直平面内摆动。已知绳刚被拉直时，绳与竖直方向成60°角。求：

（1）小球水平抛出的初速度v₀；

（2）在绳被拉紧的瞬间，支点O受到的冲量。

【答案】

（1）\(\frac{{\sqrt {6gL} }}{2}\)

（2）绳对支点O的冲量大小为m\(\sqrt {2gL} \)，方向沿绳向外。注意绳拉紧瞬间重力≪绳拉力，故忽略了重力对小球的冲量。

 

57．长为l、质量为m的柔软绳子盘放在水平桌面上，用手将绳子的一端以恒定的速度v向上提起，求当提起高度为x（x＜l）时手的作用力。

【答案】

\(\frac{x}{l}\)mg+\(\frac{m}{l}\)v²

 

58．质量为M的小车在光滑的水平地面上以v₀匀速运动。当车中的砂子从底部的漏斗中不断流下时，车子速度将（    ）。

（A）减小            （B）不变            （C）增大            （D）无法确定

【答案】

B

 

59．在光滑水平直路上停着一辆较长的木板车，车的左端站立一个大人，车的右端站立一个小孩。如果大人向右走，小孩（质量比大人小）向左走，他们的速度大小相同，则在他们走动过程中（    ）。

（A）车可能向右运动        （B）车一定向左运动

（C）车可能保持静止        （D）无法确定

【答案】

B

 

60．质量为m的平板小车静止在光滑的水平面上，一个质量为M的人立于小车的一端。当人从车的一端走向另一端的过程中，下列说法中正确的是（    ）。

（A）人对小车压力的冲量，使小车与人沿同方向运动

（B）人对小车摩擦力的冲量，使小车产生与人运动方向相反的动量

（C）人与小车的动量在任一时刻都大小相等而方向相反

（D）人与车的瞬时速度总是大小相等力向相反

【答案】

BC

 

61．质量分别为60 kg和70 kg的甲、乙两人，分别同时从原来静止的在光滑水平面上的小车两端，以3 m/s的水平初速度沿相反方向跳到地面上。若小车的质量为20 kg。则当两人跳离小车后，小车的运动速度为（    ）。

（A）19.5 m/s，方向与甲的初速度方向相同

（B）19.5 m/s，方向与乙的初速度方向相同

（C）1.5 m/s，方向与甲的初速度方向相同

（D）1.5 m/s，方向与乙的初速度方向相同

【答案】

C

 

62．质量相同的物体A、B静止在光滑的水平面上，用质量和水平速度相同的子弹a、b分别射击A、B，最终a子弹留在A物体内，b子弹穿过B，A、B速度大小分别为v_A和v_B，则（    ）。

（A）v_A＞v_B                  （B）v_A＜v_B                   （C）v_A=v_B                      （D）条件不足，无法判定

【答案】

A

 

63．在光滑的水平面上有两个静止小车，车上各站着一个运动员。两车（包含负载）的总质量均为M。设甲车上的人接到一个质量为m、沿水平方向抛来的速度为v的篮球；乙车上的人把原来在车上的一个同样的篮球沿水平方向以同样速度抛出去，则这两种情况下，甲、乙两车所获得速度大小的关系是（    ）。

（A）v_甲＞v_乙                                          （B）v_甲＜v_乙

（C）v_甲=v_乙                                （D）不同的M，m及v值结论不同

【答案】

B

 

64．质量为m=100 kg的小船静止在水面上，船上左、右两端各站着质量分别为m_甲=40 kg，m_乙=60 kg的游泳者，当他们在同一水平线上，甲朝左，乙朝右，同时以相对河岸3 m/s的速率跃入水中时，小船运动方向为_______，运动速率为_____m/s。

【答案】

向左，0.6

 

65．如图所示，将两条完全相同的磁铁分别固定在质量相等的小下上，水平面光滑，开始时甲车速度大小为3 m/s，乙车速度大小为2 m/s，方向相反并在同一直线上，当乙车的速度为零时，甲车速度为_____m/s，方向_____。

【答案】

1，向右

 

66．在水平轨道上放置一门质量为M的炮车，发射质量为m的炮弹，炮下与轨道间摩擦不计，当炮身与水平方向成θ角发射炮弹时，炮弹相对地面出射的速度为v₀，则此时炮身后退的速度v′=________。

【答案】

\(\frac{{m{v_0}\cos \theta }}{M}\)

 

67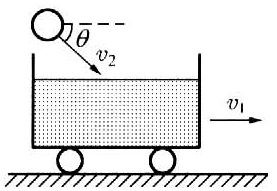．如图所示，一辆质量为M的小车以速度v₁光滑水平面上运动，一质量为m、速度为v₂物体以俯角为θ的方向落到车上并埋在车里的砂中，此时小车的速度为_____。

【答案】

\(\frac{{m{v_2}\cos \theta  + M{v_1}}}{{M + m}}\)

 

68．甲、乙两个质量都是M的小车静置在光滑水平地面上。质量为m的人站在甲车上并以速度v（对地）跳上乙车，接着仍以对地的速率v反跳回甲车。对于这一过程，下列说法中正确的是（    ）。

（A）最后甲、乙两车的速率相等

（B）最后甲、乙两车的速率之比v_甲∶v_乙=M∶（m+M）

（C）人从甲车跳到乙车时对甲的冲量I₁，从乙车跳回甲车时对乙车的冲量I₂，应是I₁=I₂

（D）选择（C）中的结论应是I₁＜I₂

【答案】

BD

 

69．一人从泊在码头边的船上往岸上跳，若该船的缆绳并没拴在码头上，则下列说法中正确的有（    ）。

（A）船越轻小，人越难跳上岸        （B）人跳跃时对船速度大于对地速度

（C）船越重越大，人越难跳上岸            （D）人跳时对船速度等于对地速度

【答案】

AB

 

70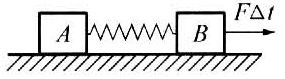．如图所示，在一个足够大的光滑平面内有 A、B 两个质量相同的木块，中间用轻质弹簧相连，今对B施以水平冲量 FΔt（Δt 极短），此后 A、B 的情况是（    ）。

（A）在任意时刻，A、B 的加速度大小相同

（B）弹簧伸长到最长时，A、B 的速度相同

（C）弹簧恢复到原长时，A、B 的动量相同

（D）弹簧压缩到最短时，系统总动能最少

【答案】

ABD

 

71．在同一高度同时释放A、B和C三个物体，自由下落距离h时，物体A被水平飞来的子弹击中，子弹留在A内；B受到一个水平方向的冲量，则A、B和C落地时间t₁、t₂和t₃的关系是（    ）。

（A）t₁=t₂=t₃                （B）t₁＞t₂＞t₃                        （C）t₁＜t₂＜t₃                        （D）t₁＞t₂=t₃

【答案】

D

 

72．火车机车拉着一列车厢以v₀速度在平直轨道上匀速前进，在某一时刻，最后一节质量为m的车厢与前面的列车脱钩，脱钩后该车厢在轨道上滑行一段距离后停止，机车和前面车厢的总质量M不变。设机车牵引力不变，列车所受运动阻力与其重力成正比，与其速度无关。则当脱离了列车的最后一节车厢停止运动的瞬间，前向机车和列车的速度大小等于______。

【答案】

\(\frac{{M + m}}{M}\)v₀

 

73．如图所示，有一条光滑轨道，其中一部分是水平的，有质量为2m的滑块A以速率15 m/s向右滑行，又有另一质量为m的滑块B从高为5 m处由静止下滑，它们在水平面相碰后，B滑块刚好能回到原出发点，则碰撞后A的瞬时速度大小为_____m/s，方向为______。

【答案】

5，水平向右

 

74．质量为M的气球下吊一架轻的绳梯，梯上站着质量为m的人。气球以v₀速度匀速上升，如果人加速向上爬，当他相对于梯的速度达到v时，气球的速度将变为______。

【答案】

v₀－\(\frac{M}{{M + m}}\)v

 

75．在光滑水平面上作直线运动的小车质量是90 kg，速度是1 m/s，一个质量60 kg的人以2 m/s的速度迎面跳上小车，并跟小车一起运动。此时车的速度为________m/s。在此过程中，人对小车的冲量大小是_____N·s，方向是_____。

【答案】

0.2，108，与车行方向相反

 

76．质量为2 kg的装砂小车，以水平速度3 m/s沿光滑水平面匀速运动。一个质量为1 kg的小球，从高0.2 m处自由落下，恰落入小车的砂中。这以后，小车的速度为______m/s。

【答案】

2

 

77．质量为30 kg的小孩推着质量为10 kg的冰车，在水平冰面上以2.0 m/s的速度滑行，不计冰面摩擦，若小孩突然以5.0 m/s的速度（对地）将冰车推出后，小孩的速度变为_______m/s。这一过程中，小孩对冰车所做的功为______J。

【答案】

1.0，105

 

78．气球质量为200 kg，载有质量为50 kg的人，静止在空中距地面20 m的地方，气球下悬一根质量可忽略不计的绳子，此人想从气球上沿绳慢慢下滑至安全到达地面，则这根绳至少多长？

【答案】

25 m

 

79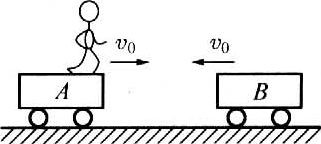．如图所示，有A、B两质量均为M的小车，在光滑的水平面上以相同的速率v₀在同一直线上相向运动，A车上有一质量为m的人，他至少要以多大的速度（对地）从A车跳到B车上，才能避免两车相撞？

【答案】

v=\(\frac{{2{M^2} + 2Mm + {m^2}}}{{(2M + m)m}}\)v₀

 

80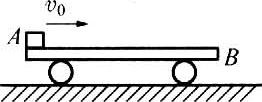．平板车B静止在光滑水平面上，在其左端另有物体A以水平初速度v₀向车的右端滑行，如图所示。由于A、B存在摩擦，则B速度达到最大时，应出现在（设B车足够长）（    ）。

（A）A的速度最小时                      （B）A、B的速度相等时

（C）A在B上相对滑动停止时        （D）B车开始作匀速直线运动时

【答案】

ABCD

 

81．汽车拉着拖车在平直的公路上匀速行驶，突然拖车与汽车脱钩，而汽车的牵引力不变，各自受的阻力不变，则在拖车停止运动前（    ）。

（A）汽车和拖车的总动量不变        （B）汽车和拖车的总动能不变

（C）汽车和拖车的总动量增加        （D）汽车和拖车的总动能增加

【答案】

AD

 

82．如图所示，质量相同的木块A和B，其间用一轻质弹簧相连，置于光滑的水平桌面上，C为竖直坚硬挡板。今将B压向A，弹簧被压缩，然后突然释放B，若弹簧刚恢复原长时，B的速度大小为v，那么当弹簧再次恢复原长时，B的速度大小应为（    ）。

（A）0          （B）v/2        （C）v          （D）\(\frac{{\sqrt 2 }}{2}\)v

【答案】

A

 

83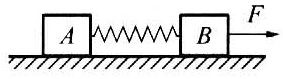．在一个足够大的光滑平面内，有两质量相同的木块A、B，中间用一轻质弹簧相连，如图所示。用一水平恒力F拉B，A、B一起经过一定时间的匀加速直线运动后撤去力F。撤去力F后，A、B两物体的情况是（    ）。

（A）在任意时刻，A、B两物体的加速度大小相等

（B）弹簧伸长到最长时，A、B的动量相等

（C）弹簧恢复原长时，A、B的动量相等

（D）弹簧压缩到最短时，系统的总动能最小

【答案】

ABD

 

84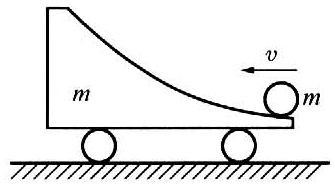．如图所示，一辆小车装有光滑弧形轨道，总质量为m，停放在光滑水平面上。有一质量也为m的速度为v的铁球，沿轨道水平部分射入，并沿弧形轨道上升h后，又下降而离开小车，离车后球的运动情况是（    ）。

（A）作平抛运动，速度方向与车运动方向相同

（B）作平抛运动，水平速度方向跟车相反

（C）作自由落体运动

（D）小球跟车有相同的速度

【答案】

C

 

85．如图所示，（a）图表示光滑平台上，物体A以初速度v₀滑到上表面粗糙的水平小车上，车与水平面间的动摩擦因数不计，（b）图为物体A与小车的v－t图像，由此可知（    ）。

（A）小车上表面至少的长度

（B）物体A与小车B的质量之比

（C）A与小车上B上表面的动摩擦因数

（D）小车B获得的动能

【答案】

ABC

 

86．质量为m=3 kg的物体在离地面高度为h=20 m处，正以水平速度v=20 m/s运动时，突然炸裂成两块，其中一块质量为m₁=1 kg，仍沿原运动方向以v₁=40 m/s的速度飞行，炸裂后的另一块的速度大小为______m/s，两块落到水平地面上的距离为______m（不计空气阻力，g取10 m/s²）。

【答案】

10，60

 

87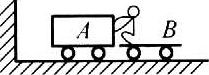．如图所示，在光滑水平面上有A、B两辆小车，水平面左侧有一竖直墙，在小车B上坐着一个小孩，车B与小孩的总质量是车A质量的10倍。从静止开始，小孩把车A以速度v（对地）推出，车A返回后，小孩抓住并再次把它推出，每次推出的小车A的速度都是v（对地）、方向向左，则小孩把车A总共推出_____次后，车A返回时，小孩不能再接到（小车与竖直墙相撞无能量损失）。

【答案】

6

 

88．甲、乙两冰船在冰面上沿一直线以相同的速度v₀（甲在前、乙在后）同向匀速滑行。今从甲船上以相对甲船v的速度水平向乙船抛出一个质量为m的砂袋，已知甲船（连操纵者、砂袋）和乙船（连操纵者）原先的质量均为M。问：当砂袋落入乙船中后两船速度各变为多大？

【答案】

v_甲＝\(\frac{{M{v_0} + mv}}{M}\)，v_乙＝v₀－\(\frac{{m(M - m)}}{{M(M + m)}}\)v

 

89．如图所示，质量为m₂和m₃的物体静止在光滑水平面上，两者之间有压缩着的弹簧，有质量为m₁的物体以v₀速度向右冲来，为了防止冲撞，m₂物体将m₃物体发射出去，m₃与m₁碰撞后粘合在一起。问m₃的速度至少应多大，才能使以后m₃和m₂不发生碰撞？

【答案】

\(\frac{{{m_1}{m_2}{v_0}}}{{({m_1} + {m_2} + {m_3}){m_3}}}\)

 

90．如图所示，两只小船平行逆向航行，航线邻近，当它们头尾相齐时，由每一只船上各投质量m=50 kg的麻袋到对而船上去，结果载重较小的一只船停了下来，另一只船则以v=8.5 m/s的速度向原方向航行。设两只船及船上的载重总重分别为m₁=500 kg、m₂=1000 kg。问在交换麻袋前两只船的速率为多大（水的阻力不计）？

【答案】

v₁=1 m/s，v₂=9 m/s

 

91．如图所示，甲、乙两辆完全一样的小车，质量都为M，乙车内用绳吊一质重为M/2的小球，当乙车静止时，甲车以速度v与乙车相碰，碰后连为一体，求刚碰后两车的速度及当小球摆到最高点时的速度。

【答案】

v/2，\(\frac{2}{5}\)v

 

92．两块光滑长木板OA与OB形成夹角α=2°的V字形，如图所示，固定在光滑的水平面上，一个小球从OB板的C点处以速度v=2 m/s并与OB板成60°的水平方向开始运动，与OA板发生碰撞后又折回OB板碰撞，已知OC=4 cm。设所有碰撞都是弹性的，试问：

（1）小球经过几次碰撞后又回到C点？

（2）此过程所经历的时间为多少？

（3）此过程中小球离O点的最近距离多大？

【答案】

（1）3次

（2）2 s

（3）2\(\sqrt 3 \) cm

 

93．相向运动的A、B两辆小车相撞后，一同沿A原来的方向前进，这是由于（    ）。

（A）A车的质量一定大于B车的质量            （B）A车的速度一定大于B车的速度

（C）A车的动量一定大于B车的动量            （D）A车的动能一定大于B车的动能量

【答案】

C

 

94．一个静止的质量为m的不稳定原子核，当它完成一次α衰变，以速度v发射出一个质量为m_α的α粒子后，其剩余部分的速度等于（    ）。

（A）－\(\frac{{{m_\alpha }}}{m}\)v        （B）－v              （C）\(\frac{{{m_\alpha }}}{{m - {m_\alpha }}}\)v             （D）－\(\frac{{{m_\alpha }}}{{m - {m_\alpha }}}\)v

【答案】

D

 

95．在两个物体碰撞前后，下列说法中可以成立的是（    ）。

（A）作用后的总机械能比作用前小，但总动量守恒

（B）作用前后总动量均为零，但总动能守恒

（C）作用前后总动能为零，而总动量不为零

（D）作用前后总动量守恒，而系统内各物体的动量增量的总和不为零

【答案】

AB

 

96．在光滑的水平面上有两个质量均为m的小球A和B，B球静止，A球以速度v和B球发生碰撞，碰后两球交换速度。则A、B球动量的改变量Δp_A、Δp_B和A、B系统的总动量的改变Δp为（    ）。

（A）Δp_A=mv，Δp_B=－mv，Δp=2mv        （B）Δp_A=Δp_B=－mv，Δp=0

（C）Δp_A=0，Δp_B=mv，Δp=mv                （D）Δp_A=－mv，Δp_B=mv，Δp=0

【答案】

D

 

97．向空中发射一物体，不计空气阻力，当此物体的速度恰好沿水平方向时，物体炸裂成a、b两块，若质量较大的a块的速度方向仍沿原来的方向，则（    ）。

（A）b的速度方向一定与原来速度方向相同

（B）在炸裂过程中，a、b受到的爆炸力的冲量一定相同

（C）从炸裂到落地这段时间里，a飞行的水平距离一定比b的大

（D）a、b一定同时到达水平地面

【答案】

D

 

98．大小相同质量不等的A、B两球，在光滑水平面上作直线运动，发生正碰撞后分开。已知碰撞前A的动量p_A=20 kg·m/s，B的动量p_B=－30 kg·m/s，碰撞后A的动量p_Aʹ=－4 kg·m/s，则：

（1）碰撞后B的动量p_Bʹ=_____kg·m/s.

（2）碰撞过程中A受到的冲量=______N·s.

（3）若碰撞时间为0.01 s，则B受到的平均冲力大小为_____N。

【答案】

（1）－6

（2）－24

（3）2400

 

99．在光滑的水平面上有A、B两个小球向右沿同一直线运动，取向右为正方向，两球的动量分别为p_A=5 kg·m/s，p_B=7 kg·m/s，如图所示。若两球发生正碰，则碰后两球的动量增量Δp_A、Δp_B可能是（    ）。

（A）Δp_A=3 kg·m/s，Δp_B=3 kg·m/s

（B）Δp_A=－3 kg·m/s，Δp_B=3 kg·m/s

（C）Δp_A=3 kg·m/s，Δp_B=－3 kg·m/s

（D）Δp_A=－10 kg·m/s，Δp_B=10 kg·m/s

【答案】

B

 

100．一个不稳定的原子核质量为M，处于静止状态。放出一个质量为m的粒子后反冲。已知放出的粒子的动能为E₀，则原子核反冲的动能为（    ）。

（A）E₀                （B）\(\frac{m}{M}\)E₀                     （C）\(\frac{m}{{M - m}}\)E₀                       （D）\(\frac{{Mm}}{{{{(M - m)}^2}}}\)E₀

【答案】

C

 

101．如图所示，两个完全相同的小球A、B用等长的细线悬于O点，线长L。若将A由图示位置静止释放，则B球被碰后第一次速度为零时的高度可能是（    ）。

（A）L/2              （B）L/4

（C）L/8              （D）L/10

【答案】

ABC

 

102．质量为m的小球A在光滑的水平面上以速度v与静止在光滑水平面上的质量为2m的小球B发生正碰，碰撞后，A球的动能变为原来的1/9，那么碰撞后B球的速度大小可能是（    ）。

（A）\(\frac{1}{3}\)v              （B）\(\frac{2}{3}\)v              （C）\(\frac{4}{9}\)v              （D）\(\frac{8}{9}\)v

【答案】

AB

 

103．质量相同的三个小球，在光滑水平面上以相同的速度运动，分别与原来静止的三个小球A、B、C、相碰（a碰A，b碰B，c碰C）。碰后a球继续沿原来方向运动；b球静止；c球被反弹而向后运动。这时A、B、C三球中动量最大的是（    ）。

（A）A球            （B）B球            （C）C球            （D）条件不足，无法判断

【答案】

C

 

104．在一条直线上相同运动的甲、乙两个小球，它们的动能相等，已知甲球的质量大于乙球的质量。它们正碰后可能发生的情况是（    ）。

（A）甲球停下，乙球反向运动               （B）甲球反向运动，乙球停下

（C）甲、乙两球都反向运动                   （D）甲、乙两球都反向运动，且动能仍相等

【答案】

AC

 

105．如图所示，在支架的圆孔上放一质量为M的木球，一质量为m的子弹以速度v从下面击中木球而穿出，使木球向上运动到h高处，求子弹穿过木球后上升的高度。

【答案】

\(\frac{{{{(mv - M\sqrt {2gh} )}^2}}}{{2{m^2}g}}\)

 

106．如图所示，在高为h的光滑平台上放一个质量为m₂的小球，另一个质量为m₁的球沿光滑弧形轨道从距平台高为h处由静止开始下滑，滑至平台上与球m₂发生正碰。若m₁=m₂，求小球m₂最终落点距平台边缘水平距离的取值范围____________。

【答案】

h＜s＜2h

 

107．一个质量为m的小球甲以速度V在光滑水平面上运动，与一个等质量的止小球乙正碰后，甲球的速度变为v，那么乙球获得的动能等于（    ）

（A）\(\frac{1}{2}\)mV²－\(\frac{1}{2}\)mv²           （B）\(\frac{1}{2}\)m(V－v)²

（C）\(\frac{1}{2}\)m(\(\frac{1}{2}\)V)²                                   （D）\(\frac{1}{2}\)m(\(\frac{1}{2}\)v)²

【答案】

B

【解析】

根据动量守恒得，mV=mv+mv′，解得v′=V-v。
所以乙球的动能E_k=\(\frac{1}{2}\)mv′²=\(\frac{1}{2}\)m(V－v)²

 

108．如图所示，木块A的右侧为光滑曲面，且下端极薄，其质量为2.0 kg，静止于光滑水平面上，一质量为2.0 kg的小球B以2.0 m/s的速度从右向左运动冲上A的曲面，与A发生相互作用。

（1）B球沿A曲面上升的最大高度（设B球不能飞出去）是（    ）。

（A）0.40 m                （B）0.20 m

（C）0.10 m                （D）0.05 m

（2）B球沿A曲面上升到最大高度处时的速度是（    ）。

（A）0                 （B）1.0 m/s         （C）0.71 m/s              （D）0.50 m/s

（3）B球与A曲面相互作用结束后，B球的速度是（    ）。

（A）0                        （B）1.0 m/s         （C）0.71 m/s              （D）0.50 m/s

【答案】

（1）C

（2）B

（3）A

 

109．在光滑的水平导轨上有A、B两球，球A追上并与球B正碰，碰前两球动量分别为p_A=5 kg·m/s，p_B=7 kg·m/s，碰后球B的动量p′=10kg·m/s，则两球质量m_A、m_B的关系可能是（    ）。

（A）m_B=m_A                 （B）m_B=2m_A                            （C）m_B=4m_A                            （D）m_B=6m_A

【答案】

C

 

110．A、B两滑块在一水平长直气垫导轨上相碰。用频闪照相机在t₀=0，t₁=Δt，t₂=2Δt，t₃=3Δt各时刻闪光四次，摄得如图所示照片，其中B像有重叠，m_B=\(\frac{3}{2}\)m_A，由此可判断（    ）。

（A）碰前B静止，碰撞发生在60 cm处，t=2.5Δt时刻

（B）碰后B静止，碰撞发生在60 cm处，t=0.5Δt时刻

（C）碰前B静止，碰撞发生在60 cm处，t=0.5Δt时刻

（D）碰后B静止，碰撞发生在60 cm处，t=2.5Δt时刻

【答案】

AB

 

111．平直的轨道上有一节车厢，车厢以12 m/s的速度作匀速直线运动。某时刻与一质量为其一半的静止的平板车挂接时，车厢顶边缘上一个小钢球向前滚出，如图所示，平板车与车厢顶高度差为1.8 m，设平板车足够长，问钢球落在平板车上何处（g取10 m/s²）？

【答案】

钢球距平板车左端距离x=s₂－s₁=2.4 m

 

112．如图所示，在光滑水平面上停有一辆质量为M的小车，车身长为l，一个质量为m的质点A放在车的尾部。A与车之间的动摩擦因数为μ，现给质点A以水平速度v₀向右运动，设A与小车的前后挡板碰撞中动能不损失。问：

（1）质点A与小车相对静止时，小车速度多大？

（2）质点A相对小车静止前与小车前后挡板碰撞的总次数是多少？

【答案】

（1）\(\frac{{m{v_0}}}{{M + m}}\)

（2）\(\frac{{Mv_0^2}}{{2\mu gl(M + m)}}\)

 

113．如图所示，一辆小车静止在光滑水平面上在C、D两端置有油灰阻挡层，整辆小车质量1 kg，在车的水平底板上放有光滑小球A和B，质量分别为m_A=1 kg，m_B=3 kg，A、B小球间置一被压缩的弹簧，其弹性势能为6 J，现突然松开弹簧，A、B小球脱离弹簧时距C、D端均为0.6 m。然后两球分别与油灰阻挡层碰撞，并被油灰粘住，问：

（1）A、B小球脱离弹簧时的速度大小各是多少？

（2）整个过程小车的位移是多少？

【答案】

（1）v_A=3 m/s，v_B=－1 m/s

（2）0.24 m

 

114．如图所示，运动的球A在光滑水平面上与一个原来静止的球B发生弹性碰撞，A、B质量关系如何，可以实现使B球获得：

（1）最大的动能；

（2）最大的速度；

（3）最大的动量。

【答案】

（1）m_A=m_B

（2）m_A≫m_B

（3）m_A≪m_B

 

115．如图所示，质量为M、半径为R的铁环放在光滑平面上，另有质量为m的小铁球，以初速v₀从O出发，而OO′=R/2，则经过多少时间小球将与铁环发生第N次弹性碰撞？

【答案】

\(\frac{{\sqrt 3 }}{{2{v_0}}}\)R(2N－1)