1．下列关于质点的说法中正确的是（    ）

（A）只要是体积很小的物体都可看作质点

（B）只要是质量很小的物体都可看作质点

（C）质量很大或体积很大的物体都一定不能看作质点

（D）由于所研究的问题不同，同一物体有时可以看作质点，有时不能看作质点

【答案】

D

 

2．一个小球从4 m高处落下，被地面弹回，在1 m高处被接住，则小球在整个运动过程中（    ）

（A）位移是5 m                 （B）路程是5 m

（C）位移大小为3 m          （D）以上均不对

【答案】

BC

 

3．关于加速度，下列说法正确的是（     ）

（A）加速度的大小与速度的大小无必然联系

（B）加速度的方向与速度的方向可能相同，也可能相反

（C）加速度很大时物体速度可能很小

（D）加速度大的物体速度变化一定很大

【答案】

ABC

 

4．关于自由落体运动，下列说法中正确的是（             ）（g取10m/s²）

（A）它是竖直向下，v₀＝0，a＝g的匀加速直线运动

（B）在开始连续的三个1 s内通过的位移之比是1∶4∶9

（C）在开始连续的三个1 s末的速度大小之比是1∶2∶3

（D）从开始运动起下落5 m、10 m、15 m，所经历的时间之比为1∶\(\sqrt 2 \)∶\(\sqrt 3 \)

【答案】

ACD

 

5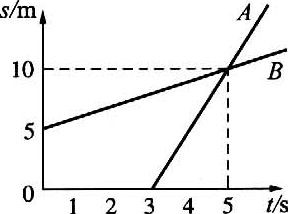．物体A、B的s－t图像如图所示，由图可知（          ）

（A）从第3 s起，两物体运动方向相同，且v_A＞v_B

（B）两物体由同一位置开始运动，但物体A比B迟3 s才开始运动

（C）在5 s内物体的位移相同，5 s末A、B相遇

（D）5 s内A、B的平均速度相等

【答案】

A

 

6．在高空自由释放甲物体后，经过时间T，在同一点再以初速v₀竖直下抛乙物体。在甲、乙两物体着地之前，关于甲相对于乙的速度，下列说法中正确的是（    ）。

（A）越来越大                   （B）越来越小

（C）保持不变                   （D）要看T和v₀的值才能决定速度变大或变小

【答案】

C

【解析】

提示：下落过程中甲物与乙物具有相同的加速度g，所以两者的相对速度保持不变

 

7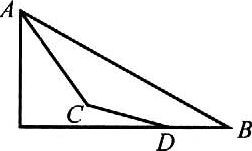．如图所示，物体从斜面上A点由静止开始下滑，第一次经光滑斜面AB滑到底端时间为t₁；第二次经光滑斜面ACD下滑，滑到底端时间为t₂，已知AC＋CD＝AB，在各斜面的等高处物体的速率相等，试判断（          ）

（A）t₁＞t₂           （B）t₁＝t₂

（C）t₁＜t₂           （D）不确定

【答案】

A

【解析】

因斜面光滑，可知物体在D点及B点速度大小相等，分别作出它们的v－t图像，根据题意，两图线与t轴围成的面积相等，即可比较两次下滑的时间长短。

 

8．在“测定匀变速直线运动加速度”的实验中，得到的记录纸带如下图所示，图中的点为记数点，在每两相邻的记数点间还有4个点没有画出，则小车运动的加速度为（   ）

（A）0.2 m/s²        （B）2.0 m/s²         （C）20.0 m/s²             （D）200.0 m/s²

【答案】

B

【解析】

提示:利用s_n－s_n－1＝aT²进行求解，T为两点间的运动时间

 

9．甲、乙两车相距s，同时同向运动，乙在前面作加速度为a₁、初速度为零的匀加速运动，甲在后面作加速度为a₂、初速度为v₀的匀加速运动，试讨论两车在运动过程中相遇次数与加速度的关系。

【答案】

答案：由于s_甲＝v₀t＋\(\frac{1}{2}\)a₂t²，s_乙＝\(\frac{1}{2}\)a₁t²，相遇时有：s_甲－s_乙＝s，则有：

v₀t＋\(\frac{1}{2}\)a₂t²－\(\frac{1}{2}\)a₁t²＝s，\(\frac{1}{2}\)（a₁－a₂）t²－v₀t＋s＝0，t＝\(\frac{{{v_0} \pm \sqrt {v_0^2 - 2({a_1} - {a_2})s} }}{{{a_1} - {a_2}}}\)    ①

（1）当a₁≤a₂时，①式t只有一个正解，则相遇一次；

（2）当a₁＞a₂时，若v₀²＜2（a₁－a₂）s，①式t无解，即不相遇；

若v₀²＝2（a₁－a₂）s，①式t只有一个解，即相遇一次。

若v₀²＞2（a₁－a₂）s，①式t有两个正解，即相遇两次

 

10．如图所示，有一个沿水平方向以加速度a作匀加速直线运动的半径为R的半圆柱体，半圆柱面上搁着一个只能沿竖直方向运动的竖直杆。在半圆柱体速度为v时，杆同半圆柱体接触点和柱心的连线与竖直方向的夹角为θ，求这时竖直杆的速度和加速度。

【答案】

v_P＝vtanθ

a_P＝\(a\frac{{\sin \theta }}{{{{\cos }^2}\theta }} - \frac{{{v^2}}}{{R{{\cos }^2}\theta }}\)

【解析】

如图所示，有一个沿水平方向以加速度a作匀加速直线运动的半径为R的半圆柱体，半圆柱面上搁着一个只能沿竖直方向运动的竖直杆。在半圆柱体速度为v时，杆同半圆柱体接触点和柱心的连线与竖直方向的夹角为θ，求这时竖直杆的速度和加速度。

 

11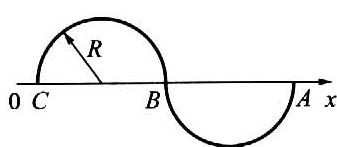．如图所示，一个质点沿两个半径为R的半圆弧由A运动到C，规定向右方向为正方向，在此过程中，它的位移和路程分别为（    ）

（A）4R，2πR                   （B）4R，－2πR

（C）－4R，2πR                （D）－4R，－2πR

【答案】

C

 

12．对于作匀速直线运动的物体，下列说法中正确的是（     ）。

（A）任意2s内的位移一定等于1 s内位移的2倍

（B）任意一段时间内的位移大小一定等于它的路程

（C）若两物体运动快慢相同，则两物体在相同时间内通过的路程相等

（D）若两物体运动快慢相同，则两物体在相同时间内发生的位移相等

 

【答案】

ABC

 

13．有关瞬时速度、平均速度、平均速率，下列说法中正确的是（    ）。

（A）瞬时速度是物体在某一位置或某一时刻的速度

（B）平均速度等于某段时间内物体运动的位移与所用时间的比值

（C）作变速运动的物体，平均速率就是平均速度的大小

（D）作变速运动的物体，平均速度是物体通过的路程与所用时间的比值

【答案】

AB

 

14．关于打点计时器的使用，下列说法中正确的是（    ）。

（A）打点计时器应用低压交流电源，交流电频率为50Hz

（B）纸带必须穿过限位孔，并注意把纸带压在复写纸的上面

（C）要先通电，后释放纸带，纸带通过后立即切断电源

（D）为减小摩擦，每次测量应先将纸带理顺

【答案】

CD

 

15．某物体沿直线向一个方向运动，先以速度v₁运动，发生了位移s，再以速度v₂运动，发生了位移s，它在整个过程中的平均速度为______。若先以速度v₁运动了时间t，又以速度v₂运动了时间3t，则它在整个过程的平均速度为______。

【答案】

\(\frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}\)，\(\frac{1}{4}\)（v₁＋3v₂）

 

16．一辆汽车在平直公路上作直线运动，先以速度v₁行驶了三分之二的路程，接着又以v₂＝20km/h跑完三分之一的路程，如果汽车在全过程的平均速度v＝28km/h，则v₁＝______km/h。

【答案】

35

 

17．一质点由位置A向北运动了4 m，又转向东运动了3 m，到达B点，然后转向南运动了1 m，到达C点，在上面的过程中质点运动的路程是多少？运动的位移是多少？位移方向如何？

【答案】

8 m，3\(\sqrt 2 \) m，正东北方向

 

18．甲、乙、丙三架观光电梯，甲中乘客看一高楼在向下运动；乙中乘客看甲在向下运动；丙中乘客看甲、乙都在向上运动。这三架电梯相对地面的运动情况可能是（    ）。

（A）甲向下、乙向下、丙向下        （B）甲向下、乙向下、丙向上

（C）甲向上、乙向上、丙向上        （D）甲向上、乙向上、丙向下

 

【答案】

CD

 

19．在下面所说的物体运动情况中，不可能出现的是（    ）

（A）物体在某时刻运动速度很大，而加速度为零

（B）物体在某时刻运动速度很小，而加速度很大

（C）运动的物体在某时刻速度为零，而其加速度不为零

（D）作变速直线运动的物体，加速度方向与运动方向相同，当物体加速度减小时，它的速度也减小

【答案】

D

 

20．甲、乙、丙三辆汽车以相同的速度经过某一路标，以后甲车一直作匀速直线运动，乙车先加速后减速运动，丙车先减速后加速运动，它们经过下一路标时的速度又相同，则（    ）

（A）甲车先通过下一个路标            （B）乙车先通过下一个路标

（C）丙车先通过下一个路标            （D）三车同时到达下一个路标

【答案】

B

【解析】

 

 

21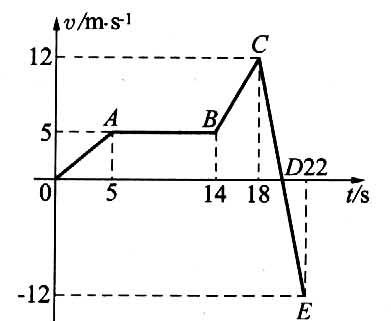．如图所示为一质点作直线运动的速度-时间图像，下列说法中正确的是（     ）

（A）整个过程中，CD段和DE段的加速度数值最大

（B）整个过程中，BC段的加速度最大

（C）整个过程中，D点所表示的状态，离出发点最远

（D）BC段所表示的运动通过的路程是34 m

【答案】

ACD

 

22．质点沿半径为R的圆周作匀速圆周运动，其间最大位移等于______，最小位移等于______，经过\(\frac{9}{4}\)圈的位移等于______。

【答案】

2R，0，\(\sqrt 2 \)R

 

23．甲、乙两地相距220 km，A车用40 km/h的速度由甲地向乙地匀速运动，B车用30 km/h的速度由乙地向甲地匀速运动。两车同时出发，B车出发后1 h，在途中暂停2 h后再以原速度继续前进，求两车相遇的时间和地点。

【答案】

4 h，离甲地160 km

 

24．一辆汽车向悬崖匀速驶近时鸣喇叭，经t₁＝8 s后听到来自悬崖的回声；再前进t₂＝27 s，第二次鸣喇叭，经t₃＝6 s又听到回声。已知声音在空气中的传播速度v₀＝340 m/s，求：

（1）汽车第一次鸣喇叭时与悬崖的距离。

（2）汽车的速度。

【答案】

（1）1400m

（2）10m/s

 

25．轮船在河流中逆流而上，下午7时，船员发现轮船上的一橡皮艇已落入水中，船长命令马上掉转船头寻找小艇。经过1 h的追寻，终于追上了顺流而下的小艇。如果轮船在整个过程中相对水的速度不变，那么轮船失落小艇的时间是何时？

【答案】

失落的时间为下午6时

 

26．一小船在河中逆水划行，经过某桥下时，一草帽落于水中顺流而下，半小时后划船人才发觉，并立即掉头追赶，结果在桥下游8 km处追上草帽，求水流速度的大小。设船掉头时间不计，划船速率及水流速率恒定。

【答案】

8 km/h

 

27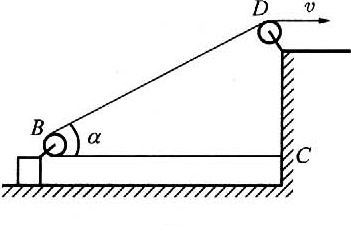．如图所示，一个带滑轮的物体放在水平面上，一根轻绳固定在C处，通过滑轮B和D牵引物体，BC水平，以水平恒速v拉绳上自由端时，物体沿水平面前进。问当跨过B的两绳夹角为α时，物体的运动速度为多大？

【答案】

v_物＝\(\frac{v}{{1 + \cos \alpha }}\)

 

28．在匀变速直线运动中，下列说法中正确的是（    ）。

（A）相同时间内位移的变化相同                   （B）相同时间内速度的变化相同

（C）相同时间内加速度的变化相同               （D）相同路程内速度的变化相同。

 

【答案】

B

 

29．下图是作直线运动物体的速度-时间图像，其中表示物体作匀变速直线运动的是图（    ）。

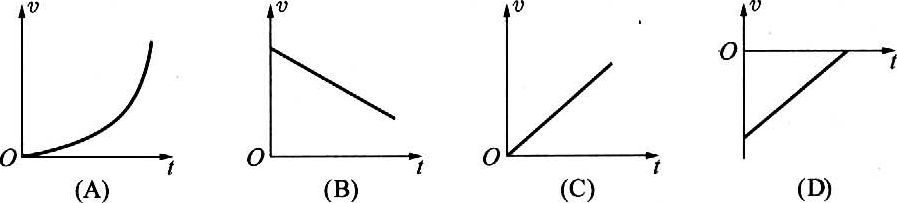
【答案】

BCD

 

30．由静止开始作匀加速直线运动的火车，在第10s末的速度为2 m/s，下列叙述中正确的是（    ）。

（A）头10 s内通过的路程为10 m            （B）每秒速度变化0.2 m/s

（C）10 s内平均速度为1 m/s                    （D）第10 s内通过2 m

【答案】

ABC

 

31．火车从车站由静止开出作匀加速直线运动，最初1 min内行驶540 m，则它在最初10 s内行驶的距离是（    ）。

（A）90 m            （B）45 m             （C）30 m             （D）15 m

【答案】

D

 

32．质点作匀加速直线运动，初速度是5 m/s，加速度是1 m/s²，那么在第4 s末的瞬时速度是______m/s，第4 s内的位移是______m。

【答案】

9，8.5

 

33．物体从光滑的斜面顶端由静止开始匀加速下滑，在最后1 s内通过了全部路程的一半，则下滑的总时间为______s。

【答案】

2＋\(\sqrt 2 \)

 

34．火车的速度为8 m/s，关闭发动机后前进70 m时速度减为6 m/s。若再经过50 s，火车又前进的距离为（     ）。

（A）50 m            （B）90 m             （C）120 m           （D）160 m

【答案】

B

 

35．一个从静止开始作匀加速直线运动的物体，从开始运动起，连续通过三段位移的时间分别是1 s、2 s、3 s，这三段位移的长度之比和这三段位移上的平均速度之比分别是（   ）

（A）1∶2²∶3²，1∶2∶3                （B）1∶2³∶3³，1∶2²∶3²

（C）1∶2∶3，1∶1∶1                   （D）1∶3∶5，1∶2∶3

【答案】

B

 

36．一物体作匀变速直线运动，速度图像如图所示，则在前4 s内（设向右为正方向）（     ）。

（A）物体始终向右运动

（B）物体先向左运动，2 s后开始向右运动

（C）前2 s物体位于出发点的左方，后2 s位于出发点的右方

（D）在t＝2 s时，物体距出发点最远

【答案】

BD

 

37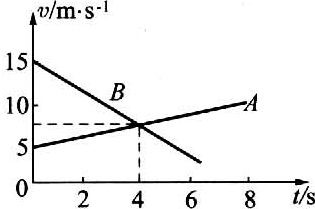．A、B两个物体在同一直线上作匀变速直线运动，它们的速度图像如图所示，则（     ）。

（A）A、B两物体运动方向一定相反

（B）头4 s内A、B两物体的位移相同

（C）t＝4 s时，A、B两物体的速度相同

（D）A物体的加速度比B物体的加速度大

【答案】

C

 

38．一质点作初速度为零的匀加速直线运动，它在第1 s内的位移为2 m，那么质点在第10 s内的位移为______m，质点通过第三个5 m所用的时间为______s。

【答案】

38，\(\frac{{\sqrt {30} {\rm{ - }}2\sqrt 5 }}{2}\)

 

39．沿平直公路作匀变速直线运动的汽车，通过连续A、B、C三根电线杆之间间隔所用的时间分别是3 s和2 s，已知相邻两电线杆间距为45 m，求汽车的加速度和通过中间电线杆时的速度。

【答案】

a＝3m/s²，v_B＝19.5m/s

 

40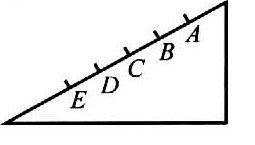．如图所示，光滑斜面AE被分成四个相等的部分，一物体由A点从静止释放，下列结论中正确的是（     ）。

（A）物体到达各点的速率v_B∶v_C∶v_D∶v_E＝1∶\(\sqrt 2 \)∶\(\sqrt 3 \)∶2

（B）物体到达各点所经历的时间t_E＝2t_B＝\(\sqrt 2 \)t_C＝\(\frac{2}{{\sqrt 3 }}\)t_D

（C）物体从A到E的平均速度\(\overline v \)＝v_B

（D）物体通过每一部分时，其速度增量v_B－v_A＝v_C－v_B＝v_D－v_C＝v_E－v_D

【答案】

ABC

 

41．一物体由静止开始作匀加速运动，它在第n秒内的位移是s，则其加速度大小为 （     ）。

（A）\(\frac{{2s}}{{2n - 1}}\)        （B）\(\frac{{2s}}{{n - 1}}\)           （C）\(\frac{{2s}}{{{n^2}}}\)              （D）\(\frac{s}{{n + 1}}\)

【答案】

A

 

42．A、B、C三点在同一直线上，一个物体自A点从静止开始作匀加速直线运动，经过B点时的速度为v，到C点时的速度为2v，则AB与BC两段距离大小之比是（     ）。

（A）1∶4            （B）1∶3            （C）1∶2            （D）1∶1

【答案】

B

 

43．一列火车由静止从车站出发作匀加速直线运动。一位观察者站在这列火车第一节车厢的前端，经过2 s，第一节车厢全部通过观察者所在位置；全部车厢从他身边通过历时6 s。设各节车厢长度相等，且不计车厢间距离，则这列火车共有______节车厢；最后2 s内从他身边通过的车厢有______节；最后一节车厢通过观察者需要的时间是_____s。

【答案】

9，5，0.34

 

44．如图所示，物体自O点由静止开始作匀加速直线运动，A、B、C、D为其轨道上的四点，测得AB＝2 m，BC＝3 m，CD＝4 m，且物体通过AB、BC、CD所用的时间相等，求OA间的距离。

【答案】

\(\frac{9}{8}\)m

 

45．在正常情况下，火车以54 km/h的速度匀速开过一个小站。现因需要，必须在这一小站停留，火车将要到达小站时，以-0.5 m/s²的加速度作匀减速运动，停留2 min后，又以0.3 m/s²的加速度出小站，一直到恢复原来的速度。求因列车停靠小站而延误的时间。

【答案】

160 s

 

46．一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以3 m/s²的加速度开始行驶，恰在这时一辆自行车以6 m/s的速度匀速驶来，从后边赶过汽车，则汽车在追上自行车之前两车相距最远距离是______m，追上自行车时汽车的速度是______m/s。

【答案】

6，12

 

47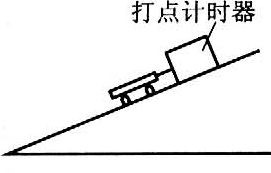．一打点计时器固定在斜面上某处，一小车拖着穿过打点计时器的纸带从斜面上滑下，如图所示。下图是打出的纸带的一段。已知打点计时器使用的交流电频率为50 Hz，利用下图给出的数据可求出小车下滑的加速度a＝______m/s²。

 

【答案】

0.40

 

48．某同学在测定匀变速直线运动的加速度时，得到了几条较为理想的纸带，已知在每条纸带每5个计时点取好一个计数点，两个计数点之间的时间间隔为0.1 s，依打点时间顺序编号为0、1、2、3、4、5，由于不小心，纸带被撕断了，如下图所示。请根据给出的A、B、C、D四段纸带回答：

（1）在B、C、D三段纸带中选出从纸带A上撕下的那段应是 ______。

（2）打A纸带时，物体的加速度大小是_____m/s²。

【答案】

（1）B

（2）6.6

 

49．物体在斜面顶端由静止匀加速下滑，最初4 s内经过的路程为s₁，最后4 s内经过的路程为s₂，且s₂－s₁＝8m，s₁∶s₂＝1∶2，求斜面的全长。

【答案】

18 m

 

50．摩托车以速度v₁沿平直公路行驶，突然驾驶员发现正前方离摩托车s处，有一辆汽车正以v₂的速度开始减速，且v₂＜v₁，汽车的加速度大小为a₂。为了避免发生碰撞，摩托车也同时减速，问其加速度a₁至少需要多大？

【答案】

a₁＝a₂＋\(\frac{{{{({v_1} + {v_2})}^2}}}{{2s}}\)

 

51．如图所示，甲、乙、丙三辆车行驶在平直公路上，车速分别为6 m/s、8 m/s、9 m/s。当甲、乙、丙三车依次相距5 m时，乙车驾驶员发现甲车开始以1 m/s²的加速度作减速运动，于是乙也立即作减速运动，丙车驾驶员也同样处理，直到三车都停下来时均未发生撞车事故。问丙车作减速运动的加速度至少应为多大？

【答案】

1.45 m/s²

 

52．有一架电梯，启动时匀加速上升，加速度为2 m/s²，制动时匀减速上升，加速度为－1 m/s²，楼高52 m。问：

（1）若上升的最大速度为6 m/s，电梯升到楼顶的最短时间是多少？

（2）如果电梯先加速上升，然后匀速上升，最后减速上升，全程共用时间为16 s，上升的最大速度是多少？

【答案】

（1）13.17 s

（2）4 m/s

 

53．A、B两站相距s，将其分成n段，汽车无初速由A站出发，分n段向B站作匀加速直线运动，第一段的加速度为a。当汽车到达每一等份的末端时，其加速度增加\(\frac{a}{n}\)，求汽车到达B站时的速度。

【答案】

\(\sqrt {\frac{{(3n - 1)as}}{n}} \)

 

54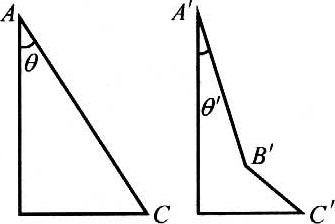．如图所示，两等高光滑的斜面AC和A′B′C′固定。已知斜面总长AC＝A′B′＋B′C′，且θ＞θ′。让小球分别从两斜面顶端无初速滑下，到达斜面底部的时间分别为t和t′。若不计在转折处的碰撞损失，则t和t′应当是什么关系？

【答案】

t＞t′

【解析】

无

 

55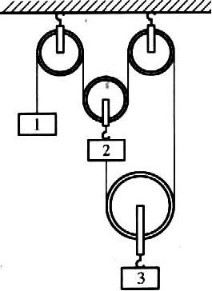．如图所示的滑轮组，物体1、2分别具有向下的加速度a₁和a₂，物体3具有向上的加速度a₃，求a₁、a₂、a₃之间的关系。

【答案】

a₃＝\(\frac{1}{2}\)（a₁＋a₂）

 

56．甲物体的重力是乙物体的3倍，它们在同一高度同时自由下落，则下列说法中正确的是（    ）

（A）甲比乙先着地                   （B）甲比乙的加速度大

（C）甲与乙同时着地        （D）甲与乙加速度一样大

【答案】

CD

 

57．一个自由下落的物体，前3 s内下落的距离是第1 s内下落距离的（    ）。

（A）2倍             （B）3倍             （C）6倍             （D）9倍

【答案】

D

 

58．关于自由落体运动，下列说法中正确的是（    ）。

（A）某段位移内的平均速度等于初速度与末速度和的一半

（B）某段时间内的平均速度等于初速度与末速度和的一半

（C）在任何相等的时间内速度的变化相等

（D）在任何相等的时间内位移的变化相等

【答案】

ABC

 

59．关于竖直上抛运动，下列说法中正确的是（    ）

（A）上升过程是减速运动，加速度越来越小；下降过程是加速运动

（B）上升时加速度小于下降时加速度

（C）在最高点速度为零，加速度也为零

（D）无论在上升过程、下落过程、最高点，物体的加速度都是g

【答案】

D

 

60．在下图中，表示物体作竖直上抛运动的是图（    ）。

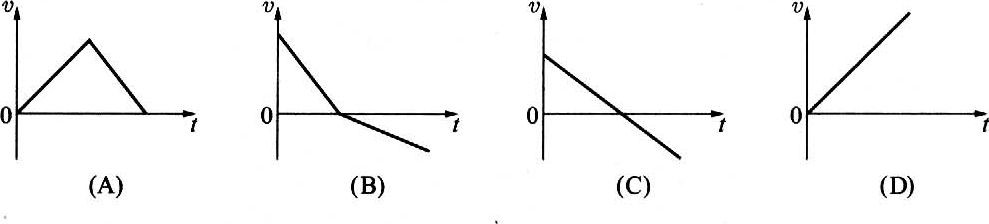
【答案】

C

 

61．一物体作自由落体运动，落地时的速度为30 m/s，则它下落高度是______m。它在前2 s内的平均速度为______m/s，它在最后1 s内下落的高度是______m（g取10m/s²）。

【答案】

45，10，25

 

62．一小球从楼顶边沿处自由下落，在到达地面前最后1s内通过的位移是楼高的\(\frac{9}{{25}}\)，求楼高。

【答案】

h＝125m

 

63．长为5 m的竖直杆下端在一窗沿上方5 m处，让这根杆自由下落，它全部通过窗沿的时间为多少（g取10m/s²）？

【答案】

（\(\sqrt 2 \)－1）s

 

64．一只球自屋檐自由下落，通过窗口所用时间Δt＝0.2 s，窗高2 m，问窗顶距屋檐多少米（g取10m/s²）？

【答案】

4.05 m

 

65．甲物体从高处自由下落时间t后，乙物体从同一位置自由下落，以甲为参照物，乙物体的运动状态是（甲、乙均未着地）（     ）。

（A）相对静止                          （B）向上作匀速直线运动

（C）向下作匀速直线运动        （D）向上作匀变速直线运动

【答案】

B

 

66．从某一高度相隔1 s先后释放两个相同的小球甲和乙，不计空气的阻力，它们在空中任一时刻（     ）

（A）甲、乙两球距离始终保持不变，甲、乙两球速度之差保持不变

（B）甲、乙两球距离越来越大，甲、乙两球速度之差也越来越大

（C）甲、乙两球距离越来越大，甲、乙两球速度之差保持不变

（D）甲、乙两球距离越来越小，甲、乙两球速度之差也越来越小

【答案】

C

 

67．竖直向上抛出一小球，3 s末落回到抛出点，则小球在第2 s内的位移（不计空气阻力）是（     ）

（A）10 m            （B）0          （C）5 m       （D）－1.25 m

【答案】

B

 

68．将一小球以初速度v从地面竖直上抛后，经4 s小球离地面高度为6 m。若要使小球抛出后经2 s达相同高度，则初速度v₀应（g取10m/s²，不计阻力）（    ）

（A）小于v         （B）大于v          （C）等于v          （D）无法确定

【答案】

A

 

69．在绳的上、下两端各拴着一小球，一人用手拿住绳上端的小球站在三层楼的阳台上，放手后小球自由下落，两小球落地的时间差为 Δt。如果人站在四层楼的阳台上，放手让球自由下落，两小球落地的时间差将（空气阻力不计）______（选填“增大”、“减小”或“不变”）。

【答案】

减小

 

70．一只球从高处自由下落，下落0.5 s时，一颗子弹从其正上方向下射击，要使球在下落1.8 m时被击中，则子弹发射的初速度为多大？

【答案】

v₀＝17.5 m/s

 

71．一石块A从80 m高的地方自由下落，同时在地面正对着这石块，用40 m/s的速度竖直向上抛出另一石块B，问：

（1）石块A相对B是什么性质的运动？

（2）经多长时间两石块相遇？

（3）相遇时离地面有多高？（g取10ms²）

【答案】

（1）匀速直线运动

（2）t＝2 s

（3）s＝60 m

 

72．从地面竖直上抛一物体，它两次经过A点的时间间隔为t_A，两次经过B点的时间间隔为t_B，则AB相距______。

【答案】

\(\frac{1}{8}\)g（t_A²－t_B²）

【解析】

无

 

73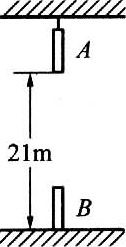．如图所示，A、B两棒各长1 m，A吊于高处，B竖直置于地面上，A的下端距地面21 m。现让两棒同时开始运动，A自由下落，B以20 m/s的初速度竖直上抛，若不计空气阻力，求：

（1）两棒的一端开始相遇的高度。

（2）两棒的一端相遇到另一端分离所经过的时间（g取10m/s²）。

【答案】

（1）h＝16 m

（2）t＝0.1 s

 

74．子弹从枪口射出时的速度大小是30 m/s，某人每隔1s竖直向上开一枪，假定子弹在升降过程中都不相碰，试求：

（1）空中最多能有几颗子弹？

（2）设在t＝0时将第一颗子弹射出，在哪些时刻它和以后射出的子弹在空中相遇而过？

（3）第一颗子弹在距枪口多高的地方依次与这些子弹相遇（不计空气阻力）？

【答案】

（1）6颗子弹

（2）t₁₂＝3.5 s；t₁₃＝4.0 s；t₁₄＝4.5 s；t₁₅＝5.0 s；t₁₆＝5.5 s（t₁₂表示第1颗子弹与第2颗子弹在空中相遇的时间）

（3）h₁₂＝43.75 m；h₁₃＝40 m；h₁₄＝33.75 m；h₁₅＝25 m；h₁₆＝13.75 m

【解析】

无

 

75．从匀速上升的直升机上落下一个物体，下列说法中正确的是（    ）。

（A）从地面上看，物体作自由落体运动

（B）从飞机上看，物体作竖直上抛运动

（C）物体和飞机之间的距离开始减小，后来增大

（D）物体落地时的速度一定大于匀速上升的飞机的速度

【答案】

D

 

76．一矿井深125 m，在井口每隔一定时间自由下落一个小球，当第11个小球刚从井口下落时，第1个小球恰好到井底，则相邻两小球下落的时间间隔为多大？这时第3个小球与第5个小球相距多少米？

【答案】

0.5 s，35 m

 

77．将一链条自由下垂悬挂在墙上，放开后让链条作自由落体运动。已知链条通过悬点下3.2 m处的一点历时0.5 s，问链条的长度为多少？

【答案】

2.75 m

 

78．利用水滴下落可以测出当地的重力加速度g，调节水龙头，让水一滴一滴地流出，在水龙头的正下方放一盘子，调节盘子的高度，使一个水滴碰到盘子时恰好有另一水滴从水龙头开始下落，而空中还有一个正在下落中的水滴。测出水龙头到盘子间距离为h，再用秒表测时间，以第一个水滴离开水龙头开始计时，到第N个水滴落在盘中，共用时间为t，则重力加速度g＝_________。

【答案】

\(\frac{{{{(N + 1)}^2}h}}{{2{t^2}}}\)

 

79．小球A从距地高h的地方自由下落，同时以速度v₀把小球B从地面A的正下方竖直上抛，求A、B两球在空中相遇应当满足的条件。

【答案】

\(\frac{{\sqrt {2gh} }}{2}\)＜v₀＜\({\sqrt {gh} }\)

 

80．在某处以速度2v₀竖直上抛出A球后，又以速度v₀竖直向上抛出B球，要使两球能在空中相遇，两球抛出的时间间隔Δt应满足什么条件（空气阻力不计）？

【答案】

\(\frac{{2{v_0}}}{g}\)≤Δt≤\(\frac{{4{v_0}}}{g}\)

 

81．小球A从地面以初速度v₀₁＝10 m/s竖直上抛，同时小球B从一高为h＝4m的平台上以初速v₀₂＝6 m/s竖直上抛。忽略空气阻力，两球同时到达同一高度的时间、地点和速度分别为多少？

【答案】

t＝1 s，h＝5 m，v_A＝0，v_B＝-4 m/s（负号表示B球运动方向向下）

 

82．拧开水龙头水就会流出来，为什么连续的水流柱的直径在下流过程中会变小？设水龙头的开口直径为1 cm，安装在离地面75 cm高处，若水龙头开口处水的流速为1 m/s，那么水流柱落到地面的直径应为多少？

【答案】

在时间t内，通过任一水流柱截面的水的体积是一定的。因水流柱顶点的水流速小于下面部分的水流速，因此水柱直径上面比下面大。

0.5 cm

 

83．一弹性小球自5 m高处自由下落，掉在地板上，每与地面碰撞一次，速度减小到碰撞前速度的\(\frac{7}{9}\)，不计每次碰撞的时间，计算小球从开始下落到停止运动所经过的路程、时间和位移（g取10 m/s²）。

【答案】

20.3 m，8 s，5 m，方向向下