1．关于位移和路程，下列说法中正确的是（    ）

（A）位移相同，路程可以不同；路程相同，位移可以不同

（B）路程总不小于位移的大小

（C）物体作直线运动时路程和位移大小一定相等

（D）物体作不改变运动方向的直线运动时路程和位移相同

【答案】

AB

 

2．关于速度和加速度，下列说法中正确的是（       ）

（A）速度方向改变了，加速度方向一定改变

（B）加速度大的物体运动得快

（C）加速度减小时速度也一定减小

（D）加速度不变时速度可以改变

【答案】

D

 

3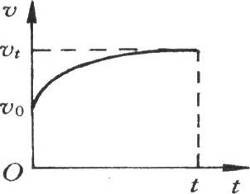．某质点初速为v₀，沿直线运动的v-t图如图所示。经时间t后速度为v_t。则对于时间t内质点的平均速度\(\bar v\)和加速度a有下列结论，其中正确的是（    ）

（A）\(\bar v\)＝\(\frac{{{v_0} + {v_t}}}{2}\)               （B）\(\bar v\)＞\(\frac{{{v_0} + {v_t}}}{2}\)

（C）a越来越大                （D）a越来越小

【答案】

BD

 

4．以10 m/s速度行驶的汽车，急刹车产生的加速度大小为5 m/s²。则刹车后3 s内汽车的位移为（     ）

（A）7.5m           （B）10m             （C）20m             （D）52.5m

【答案】

B

 

5．物体沿直线从A点经B点运动到C。在AB段运动速度为60 m/s，在BC段运动速度为30 m/s，且AB＝3BC。则AC段中平均速度大小为（    ）

（A）37.5 m/s              （B）45 m/s         （C）48 m/s         （D）52.5 m/s

【答案】

C

 

6．一物体由静止起作匀加速运动，试计算下列各小题：

（1）速度为4 m/s时，位移为8 m；速度为8 m/s时，位移为______。

（2）速度为2 m/s时，位移为5 m；要使速度达到6 m/s，还要走______。

（3）前5 s内走10 m，则前10s内走_____。

（4）前4 s内走10 m，则再走4 s还能走________。

（5）走前2 m需4 s，走前4 m需_______。

（6）走前3 m需5 s。再走3 m还要________。

（7）第一个5 s走8 m，第十个5 s走______。

（8）通过10 m时，速度达到2 m/s，再走10 m速度达到______。

（9）前2 s内位移和后3 s（共走5 s）内位移之比为_____。

（10）共走5 m，通过前2 m所需时间和通过后3 m所需时间之比为_______。

【答案】

（1）32 m

（2）40 m

（3）40 m

（4）30 m

（5）4\(\sqrt 2 \) s

（6）5（\(\sqrt 2 \)－1）s

（7）152 m

（8）2\(\sqrt 2 \) m/s

（9）4∶21

（10）\(\sqrt 2 \)∶\(\sqrt 5 \)－\(\sqrt 2 \)

 

7．物体作匀减速运动3 m停下，它通过前1 m、前2 m、前3 m所需时间之比为_______，前1 m、前2 m、前3 m内平均速度之比为_______，通过第1 m、第2 m、第3 m所需时间之比为______。

【答案】

\(\sqrt 3 \)－\(\sqrt 2 \)∶\(\sqrt 3 \)－1∶\(\sqrt 3 \)，\(\sqrt 3 \)＋\(\sqrt 2 \)∶\(\sqrt 3 \)＋1∶\(\sqrt 3 \)，\(\sqrt 3 \)－\(\sqrt 2 \)∶\(\sqrt 2 \)－1∶1

 

8．自由落体第100 s内位移和第1 s内位移之比为______，自由落体通过第100 m所需时间和通过第1 m所需时间之比为_____。

【答案】

199∶1，10－\(\sqrt 99 \)∶1

 

9．离地高96 m处，每隔相等时间自由下落一物体，第5个物体放出时第1个物体恰好落地，则此时它们在空中的高度依次为_____m、______m、______m、______m、_______m。

 

【答案】

0，42，72，90，96

 

10．从静止开始作匀变速直线运动的物体前3s内通过的位移为s，物体通过第2s内后1/3位移所用时间为t₁，通过第3s内后1/5位移所用的时间为t₂，则t₁∶t₂为（    ）

（A）16∶81                      （B）7∶17

（C）\(\sqrt 3 \)∶2\(\sqrt 2 \)                （D）2－\(\sqrt 3 \)∶3－2\(\sqrt 2 \)

【答案】

D

【解析】

把第2s内位移两等分，把第3s内位移三等分，则每段位移都相等，可用比例解

 

11．一质点作匀加速直线运动，在第1个Δt时间内位移为s₁，第2个Δt时间内位移为s₂，求该质点运动的加速度及这两段时间的中间时刻的瞬时速度。

【答案】

\(\frac{{{s_2} - {s_1}}}{{\Delta {t^2}}}\)，\(\frac{{{s_2} + {s_1}}}{{2\Delta t}}\)

 

12．一质点作匀加速度直线运动通过一段位移，其初速为v₀，末速为v_t。求该段位移的中间位置时的速度。

【答案】

\(\sqrt {\frac{{v_0^2 + v_t^2}}{2}} \)

 

13．如果乘客在地铁列车中能忍受的最大加速度值是1.4m/s²，如果两相邻地铁车站相距560m，求地铁列车在这两站间行驶的最短时间为多少？最大行驶速度为多大？

【答案】

40 s，28 m/s

 

14．一质点作匀加速运动，在最初两个连续的4 s内发生的位移分别为24 m和64 m。求其加速度和初速度。

【答案】

2.5 m/s²，1 m/s

 

15．物体由静止开始作匀加速运动，第n秒内通过的位移为s。求它的加速度a和第n秒初的速度。

 

【答案】

\(\frac{{2s}}{{2n - 1}}\)，\(\frac{{2s(n - 1)}}{{2n - 1}}\)

 

16．一质点作初速为零的匀变速直线运动，若其第2 s内位移是s，则其加速度大小为______，第3 s的初速度大小为_____，第4 s内的平均速度为_____。

【答案】

\(\frac{2}{3}\)s，\(\frac{4}{3}\)s，\(\frac{7}{3}\)s

 

17．一质点作初速为零的匀加速直线运动。若其第7 s内位移比第6 s内位移多2 m，则其第7 s内位移大小为_______m，前7 s内位移大小为______m，加速度大小为_____ m/s²，第7 s内位移比第1s内位移多_______m。

【答案】

13，49，2，12

 

18．作匀加速直线运动的物体，加速度大小为2 m/s²，若其第1 s内位移是2 m，则第3 s内位移是_______m，3 s内的平均速度大小是________m/s，第4 s初的速度大小是_______m/s，初速度大小为_________m/s。

【答案】

6，4，7，1

 

19．甲、乙两车同时同向由同地出发运动，甲以10 m/s的速度匀速运动，乙匀加速运动，10 s末追上甲，再过10 s超过甲100 m，求乙追上甲时的速度大小和乙的加速度。

【答案】

15 m/s，1 m/s²

【解析】

（提示：所求速度为这20 s内的中间时刻速度，就等于这20 s内的平均速度）

 

20．一物体作匀加速直线运动，前一半位移的平均速度为3 m/s，后一半位移的平均速度为6 m/s，则其通过中间位置时的速度大小为多少？

【答案】

5 m/s

【解析】

（提示：由前一半位移的中间时刻速度为3 m/s，后一半位移的中间时刻速度为6 m/s，可作出其v-t图，再由相似三角形对应边成比例求解）

 

21．自由落体最后1 s通过的位移为65 m，求其下落总高度。

【答案】

245 m

 

22．物体自由下落，最后2 s内下落高度为全部下落高度的\(\frac{3}{4}\)，则它下落的总高度为________m，下落的总时间为______s。

【答案】

80，4

 

23．一物体从离地高处自由下落，将分成高度相等的三段，则自上而下经过每段高度所用的时间之比为（    ）

（A）1∶0.414∶0.318        （B）1∶\(\sqrt 2 \)∶\(\sqrt 3 \)     （C）1∶3∶5              （D）1∶4∶9

【答案】

A

 

24．A球自塔顶自由下落a时，B球自塔顶下距塔顶b处开始下落，两球同时落地。则塔高为_____。

【答案】

\(\frac{{{{(a + b)}^2}}}{{4a}}\)

 

25．一物体自由下落，先后经过A、B、C三点，相隔时间相等，已知AB＝23 m，BC＝33 m，求物体起落点离A点的高度。

【答案】

16.2 m

【解析】

提示∶用打点计时器实验公式解较方便

 

26．作初速为零的匀加速直线运动的物体，在前4 s内的位移为16 m，最后4 s内的位移为32 m，试求∶

（1）该物体运动时的加速度大小；

（2）在这段时间内的总位移大小。

【答案】

2，36

 

27．A、B两车同向在一条平直公路上行驶，A在B的后面相距s处作速度为v的匀速运动；同时B作初速为零、加速度为a的匀加速直线运动。则v、a、s满足什么条件时，两车可以相遇两次？

【答案】

v²＞2as

 

28．物体初速为v₀，以加速度a作匀加速直线运动，某段时间的末速为初速的n倍，则该段时间内的位移为____。

【答案】

\(\frac{{v_0^2({n^2} - 1)}}{{2a}}\)

 

29．某质点作直线运动，其位移和时间关系为s＝30t－5t²。，其中t的单位是s，s的单位是m，则可知其加速度为____m/s²，第3 s初的速度为____m/s。

【答案】

-10，10

 

30．汽车从静止起作匀加速运动，第4 s末关闭发动机，再经6 s后停止，经过的位移共为30 m。则前后两段运动的加速度分别为________m/s²、________m/s²。

【答案】

1.5，－1

 

31．一辆汽车以加速度a起动时，有一辆自行车刚好以速度v匀速从旁边驶过，汽车追上自行车所需时间为______，追上时汽车的速度大小为______。

【答案】

\(\frac{{2v}}{a}\)，2v

 

32．汽车以20 m/s的速度作匀速直线运动，刹车后加速度的大小为5 m/s²，那么刹车后2s内与6 s内汽车的位移之比为__________。

【答案】

3∶4

 

33．光滑斜面AB被划分为距离相等的五段，一物体从顶端A由静止开始下滑，若通过第1段所需时间为t₁，通过第5段所需时间为t₅，则t₅∶t₁＝______。

【答案】

\(\sqrt 5 \)-2

 

34．以v₁速度行驶的汽车司机发现在车前面相距s处有一辆卡车以v₂速度行驶时即刹车，刹车后加速度大小为a，恰未相碰，则s应为_____。

【答案】

\(\frac{{{{({v_1} - {v_2})}^2}}}{{2a}}\)

 

35．从塔顶落下一小球，它在最后1 s内的位移是30 m，则小球落地时速度是___m/s，塔顶的高度是_____m。

【答案】

35，61.25

 

36．关于位移和路程的关系，正确的说法有（    ）

（A）物体沿直线向一个方向运动时通过的路程和位移完全相同

（B）物体通过的路程不相等时位移可能相同

（C）物体通过一段路程其位移可能为零

（D）几个物体有相同的位移时它们的路程也一定相同

【答案】

BC

 

37．下述说法中可能的有（   ）

（A）某时刻物体的速度很大加速度却很小

（B）某时刻物体的加速度很大速度却很小

（C）某段时间内加速度变化很大而速度不变

（D）某段时间内速度变化很大而加速度不变

【答案】

ABD

 

38．汽车沿直线由A运动到B再运动到C，AB段平均速度为v₁，运动时间为t₁，BC段平均速度为v₂，运动时间为t₂，则（     ）

（A）若AB＝BC，AC段平均速度为\(\frac{{{v_1} + {v_2}}}{2}\)

（B）若t₁＝t₂，AC段平均速度为\(\frac{{{v_1} + {v_2}}}{2}\)

（C）若t₁＝t₂，AC段平均速度为\(\frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}\)

（D）不管AB＝BC还是t₁＝t₂，AC段平均速度都是\(\frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}\)

【答案】

B

 

39．一物体以初速v₀加速度a作匀加速直线运动，a和v₀同向，当a的大小逐渐减小时，则（     ）

（A）速度和总位移都减小                      （B）速度减小总位移增大

（C）速度增大总位移减小                      （D）速度和总位移仍都增大

【答案】

D

 

40．甲、乙、丙三质点运动的s－t图如图所示，则在时间0～t₁内（    ）

（A）甲的位移最大                   （B）三者位移相同

（C）乙、丙路程相同               （D）三者路程相同

【答案】

BC

 

41．物体先作初速为零的匀加速运动，加速度为a₁、时间t₁运动了距离s₁后速度达到v₁，然后改作加速度大小为a₂的匀减速运动，时间t₂运动了距离s₂而停下，则（    ）

（A）\(\frac{{{s_1}}}{{{s_2}}}\)＝\(\frac{{{t_1}}}{{{t_2}}}\)       （B）\(\frac{{{a_1}}}{{{a_2}}}\)＝\(\frac{{{t_1}}}{{{t_2}}}\)       （C）\(\frac{{{s_1}}}{{{t_2}}}\)＝\(\frac{{{s_2}}}{{{t_2}}}\)＝\(\frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}}\)       （D）v＝\(\frac{{{s_1}{t_2} + {s_2}{t_1}}}{{{t_1}{t_2}}}\)

【答案】

ACD

 

42．100 m赛跑中，某学生12.5 s跑完全程，他中间时刻的速度是7.8 m/s，到达终点时速度是9.2 m/s。则他在全程中的平均速度是（    ）

（A）8.1 m/s （B）7.8 m/s  （C）8 m/s    （D）9.2 m/s

【答案】

C

【解析】

无

 

43．物体做自由落体，先后经过空中M、N两点时的速度分别为v₁、v₂，则下列说法中正确的是（      ）

（A）MN间的距离为\(\frac{{v_2^2 - v_1^2}}{{2g}}\)

（B）经过MN的平均速度为\(\frac{{{v_1} + {v_2}}}{2}\)

（C）经过MN所需时间为\(\frac{{{v_2} - {v_1}}}{g}\)

（D）经过MN中点时的速度为\(\frac{{{v_1} + {v_2}}}{2}\)

【答案】

ABC

 

44．汽车沿平直公路做匀加速直线运动，路旁每两根电线杆之间的距离均为45 m，汽车通过第一个间隔历时5 s，通过第二个间隔历时4 s，则汽车运动的加速度大小为         m/s²。

【答案】

0.5

 

45．物体运动的前一半路程平均速度为v₁，后一半路程平均速度为v₂。试证明，无论v₂多大，全程的平均速度必定小于2v₁。

【答案】

略

 

46．一列火车以v的平均速度从甲地驶到乙地所需时间为t，现在火车以v₀速度匀速由甲地出发，中途急刹车后停止，又立即加速到v₀。从刹车起直到加速到v₀所用时间为t₀，设刹车过程和加速过程的加速度大小相等，如果仍要使火车在t时间内到达乙地，求：火车匀速运动的速度v₀。

【答案】

\(\frac{{2vt}}{{2t - {t_0}}}\)

 

47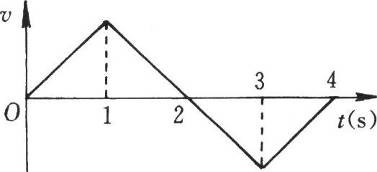．某质点的v-t图如图所示，则它离出发点最远的时刻为_______，回到出发点的时刻为________。

【答案】

2 s末，4 s末

 

48．一物体由静止开始作匀加速直线运动，已知在第2 s内的平均速度大小为0.6 m/s，则物体的加速度大小是______m/s²。

【答案】

0.4

 

49．物体作匀加速直线运动先后经过A、B、C三点，经过AB段所需时间为t，经过BC段所用时间为\(\frac{t}{2}\)。若AB＝BC＝s，则物体运动全过程的平均速度为_____，运动的加速度大小为_____。

【答案】

\(\frac{{4s}}{{3t}}\)，\(\frac{{8s}}{{3{t^2}}}\)

 

50．作匀加速直线运动的物体，先后经过A、B两点时速度分别为v和7v，则通过AB中间时刻的速度是____，通过AB中间位置时的速度是______。如果通过AB的时间为t，前\(\frac{t}{2}\)的位移为s₁、后\(\frac{t}{2}\)的位移为s₂，则s₂－s₁＝_______。

【答案】

4v，5v，0.5vt

 

51．作匀减速运动的物体，初速为3 m/s，加速度为-0.4 m/s²，某1 s内的位移为0.4 m，则在这1 s前，物体已经运动了_______s。

【答案】

6

 

52．一小球沿斜面滑下，依次经过A、B、C三点，已知AB＝6 m，BC＝10 m，小球经过AB和BC所用时间均为2 s，则小球在经过A、C两点时的速度分别为_____m/s和________m/s。

【答案】

2，6

 

53．一物体以初速v₀作匀减速运动3 s内停下，则它前1 s内、前2 s内、前3 s内的平均速度之比为_________。

 

【答案】

5∶4∶3

 

54．甲车以10 m/s初速度及大小为4 m/s²的加速度作匀减速直线运动，乙车由同地同时同向出发作初速为零加速度为1 m/s²的匀加速直线运动，则它们出发后再次相遇所需时间为______s。

【答案】

5

 

55．质点由M点出发作匀加速直线运动，某时刻经过A点，再经过时间n到达B点，再经过时间n到达C点，再经过时间n到达D点，又已知MA＝a，MB＝b，MC＝c，MD＝d，则（     ）

（A）c－b＝3（b－a）                     （B）d－a＝3（c－b）

（C）b＋d＝2c                                 （D）质点运动的加速度为\(\frac{{a + c - 2b}}{{{n^2}}}\)

【答案】

BD

 

56．一个作直线运动的物体，其加速度逐渐减小直到变为零的过程中，此物体的运动情况可能是（      ）

（A）速度不断增大，最后作匀速运动

（B）速度不断减小，最后静止

（C）速度不断减小，然后反向加速，最后作匀速运动

（D）速度不断减小，最后作匀速运动

【答案】

ABCD

 

57．在某高度h₁处，自由下落一物体A，1 s后从另一较低高度h₂处，自由下落另一物体B，若A从开始下落起下落了45 m时赶上B，并且再过1 s到地，则B从下落到着地所经历的时间是（     ）

（A）3 s                      （B）约3.3 s        （C）3.5 s                   （D）4 s

【答案】

B

 

58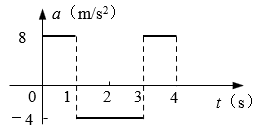．一物体沿一直线从静止开始运动且同时开始计时，其加速度随时间变化关系如图所示。则关于它在前4 s内的运动情况，下列说法中正确的是（    ）

（A）前3 s内先加速后减速，3 s末回到出发点

（B）第3 s末速度为零，第4 s内反向加速

（C）第1 s和第4 s末，物体的速度均为8 m/s

（D）前4 s内位移为16 m

【答案】

CD

 

59．从静止开始作匀变速直线运动的物体3 s内通过的位移为s，设物体在第2 s内后1/3时间里以及第3 s内后1/3时间里通过的位移分别为s₁和s₂，则s₁∶s₂为（     ）

（A）5∶11         （B）3∶7           （C）11∶17        （D）7∶13

【答案】

C

【解析】

提示：把第2 s时间分成三等分，把第3 s时间也三等分后再用比例

 

60．甲、乙两质点同时开始在同一水平面上同方向运动，甲在前，乙在后，相距s。甲初速度为零，加速度为a，作匀加速直线运动，乙以速度v₀作匀速直线运动，则下列判断正确的是（    ）

（A）乙一定能追上甲

（B）当它们速度相等时相距最近

（C）乙若能追上甲，则追上时乙的速度必定大于或等于甲的速度

（D）它们一定有两次相遇

【答案】

C

 

61．跳伞运动员离开飞机后先作自由落体运动，到离地125 m高处打开降落伞，此后他以14.3 m/s²加速度着陆，到达地面时速度为5 m/s，求：

（1）离开飞机时高度；

（2）离开飞机后经多少时间到达地面。

【答案】

（1）305 m

（2）9.85 s

 

62．摩托车的最大速度是30 m/s，要想从静止开始用3 min的时间追上前面100 m处以20 m/s速度匀速行驶的汽车，则摩托车的加速度应为多大？

 

【答案】

0.265 m/s²（提示∶摩托车先加速后匀速）

 

63．平直公路上甲、乙两汽车沿同方向运动，乙车以3 m/s的速度作匀速直线运动，当乙车在甲车前面4 m处时甲车从静止开始以2 m/s²的加速度作匀加速直线运动，当甲车追上乙车后立即以-4 m/s²加速度作匀减速直线运动，试问乙车再追上甲车还要经历多少时间？

 

【答案】

2.67 s

 

64．降落伞在下落一定时间以后的运动是匀速的，没风时某跳伞运动员着地时的速度是5 m/s。现在有风，风使他以4 m/s的速度沿水平方向向东移动，他的着地速度大小为______m/s，方向________。

【答案】

6.4，东偏下arctan1.25

 

65．河宽100 m，水速3 m/s，小船在静水中速度为5 m/s，小船垂直河岸划时，船实际运动的速度大小为_____m/s，过河所需时间为______s。到达对岸时向下游方向走了______m。为使小船尽快到达对岸，小船划行方向应是______，为使小船到达正对岸，则划行方向又应是______。

【答案】

5.83 ，20 ，60 ，垂直于河岸，偏向上游与河岸成53°角

 

66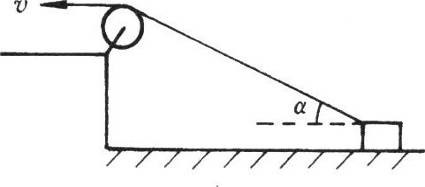．如图所示，一物体放在水平面上，用细绳跨过滑轮向左拉动，设绳子向左拉动的速度恒为v，则物体向左运动的速度大小将_______（填“增大”、“不变”或“减小”），当物体运动到细绳与水平面成α角时物体运动的速度大小为_______。

【答案】

增大，\(\frac{v}{{\cos \alpha }}\)

 

67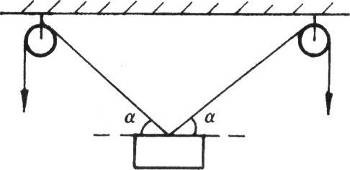．如图所示，一物体被两根绕过滑轮的细绳对称地向上提升，若要使物体以速度v匀速上升，则两端细绳向下拉的速度将_______（填“增大”、“不变”或“减小”），当细绳与水平方向成α角时绳端向下拉的速度大小为_______。

【答案】

减小，vsinα

 

68．一木块长为L、以速度v匀速随水平传送带向右运动，一子弹以速度v₁，向右射入木块，穿出时速度为v₂，则子弹在木块中的运动时间为______。若子弹是向左射入木块的，其他条件不变，则子弹在木块中运动的时间又为______。

【答案】

\(\frac{{2L}}{{{v_1} + {v_2} - 2v}}\)，\(\frac{{2L}}{{{v_1} + {v_2} + 2v}}\)

 

69．竖直向上射出的箭，初速度是35 m/s，空气阻力不计，能上升的最大高度是______m，从射出到落回原地一共用时间_______s，落回原地的速度大小为______m/s。

 

【答案】

61.25，7，35

 

70．竖直上抛物体到达其所能到达的最大高度的一半时速率为14 m/s，则物体能上升的最大高度为_______m，抛出1 s末物体的速度大小为______m/s，加速度大小为_________m/s²，抛出3 s末的速度大小为_______m/s，加速度大小为______m/s²，落地前最后0.5 s内的平均速度的大小为______m/s。

【答案】

20，10，10，10，10，17.5

 

71．某物作竖直上抛运动，经过抛出点之上0.4 m处时速度为3 m/s，当它经过抛出点之下0.4 m处时速度大小为______m/s。

【答案】

5

 

72．一氢气球以加速度a＝2 m/s²由静止起自地面匀加速竖直上升，到100 m高处时掉出一物体，空气阻力不计，掉出的物体离开气球时的速度大小为______m/s，离开气球时物体的加速度大小为_____m/s²，物体经时间_____s落地。

【答案】

20，10，9

 

73．一物以30 m/s的初速自地面起作竖直上抛运动，2 s后另一物也以30 m/s的初速自地面起作竖直上抛运动，则两物相遇时速度大小为______m/s，相遇时两物离地高为_______m。

【答案】

10，40

 

74．物体A和B分别于离地h和2h高处水平抛出，初速分别为2v₀和v₀，空气阻力不计，则它们飞行时间之比为________，水平射程之比为________，落地时水平速度之比为______，落地时竖直速度之比为______。

【答案】

1∶\(\sqrt 2 \)，\(\sqrt 2 \)∶1，2∶1，1∶\(\sqrt 2 \)

 

75．物体作平抛运动，计算下列各题（h为高度，s为水平位移）:

（1）已知h＝5 m、v₀＝15 m/s，则s＝_______m。

（2）已知h＝20 m、s＝30 m，则v₀＝_______m/s。

（3）已知v₀＝20 m/s、v₁＝25 m/s，则h＝_______m。

（4）已知h＝20 m、v_t＝25 m/s，则v₀＝_______m/s。

（5）已知h＝45 m、末速与水平成37°，则v₀＝_______m/s。

（6）已知前3 s内s＝h，则v₀＝_______m/s。

（7）已知第4 s末速大小为50 m/s，则v₀＝_______m/s。

（8）已知s＝120 m，末速与水平成37°，则v₀＝_______m/s。

【答案】

（1）15（2）15（3）11.25（4）15（5）40（6）15（7）30（8）40

 

76．已知作平抛运动的物体在飞行过程中经过A、B两点的时间内速度改变量的大小为Δv，A、B两点的竖直距离为Δy，则物体从抛出到运动到B点共经历了多少时间 ？

【答案】

\(\frac{{2g\Delta y + {{(\Delta v)}^2}}}{{2g\Delta v}}\)

 

77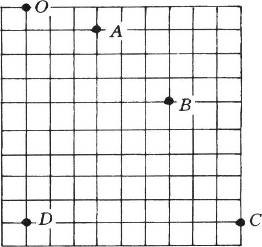．如图所示，闪光照片记下了作平抛运动的小球的四个位置O，A，B，C。其中O为抛出点，OD为竖直线，闪光间隔时间为\(\frac{1}{{30}}\) s。求：

（1）小球从O运动到C所需时间；

（2）小球在这段时间内的竖直位移；

（3）小球抛出时的初速.

【答案】

（1）0.1 s

（2）0.05 m

（3）0.5 m/s

 

78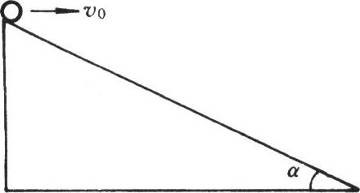．如图所示，一物体自倾角为α＝37°的斜面顶端以初速v₀＝10 m/s水平抛出，空气阻力不计。经过时间_______，物体离开斜面最远，最远距离为______，经过_______物体落到斜面上。

【答案】

0.75 s（提示∶可将平抛运动沿平行于斜面和垂直于斜面分解），2.25 m，1.5 s

 

79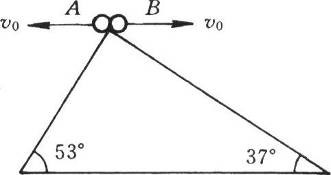．如图所示，相对的两个斜面倾角分别为37°和53°，在顶点把两个小球以同样大小的初速分别向左、右两边水平抛出，小球均落在斜面上。若不计空气阻力，则A、B两个小球从抛出到落在斜面上所用时间之比为多大？

【答案】

16∶9

 

80．作平抛运动的物体，从抛出开始，当水平位移与竖直位移的大小之比为4∶5时，水平速度与竖直速度的大小之比为________。

 

【答案】

2∶5

 

81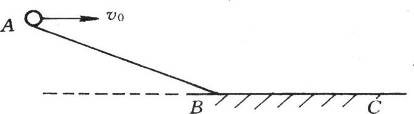．如图所示，AB为一斜面，BC为一水平面，从A点以水平初速v向右抛出一小球，其落点与A点的水平距离为s₁，从A点以水平初速2v向右抛出一小球，其落点与A点的水平距离为s₂，不计空气阻力，则s₁∶s₂可能为（    ）

（A）1∶2            （B）1∶3            （C）1∶4            （D）1∶5

【答案】

ABC（提示：可能都落在斜面上，也可能都落在水平面上，也可能一个落在斜面上一个落在水平面上）

 

82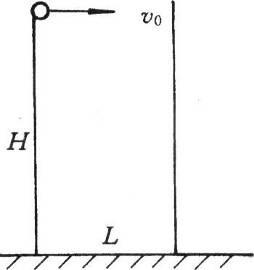．如图所示，从高H＝40 m的光滑墙的顶端，以初速v₀＝10 m/s把一个弹性小球沿水平方向对着相距L＝4 m的另一竖直光滑墙抛出。设球与墙碰撞前后垂直于墙的速度大小不变、方向相反，而平行于墙的速度保持不变，空气阻力不计，则物体从抛出到落地的过程中与墙碰撞_____次。

【答案】

7（提示∶与墙碰后弹回的轨迹可以墙为轴翻转后与原来轨迹相连仍为一抛物线）

 

83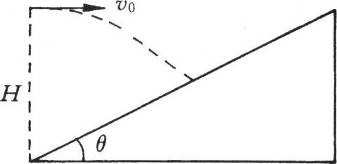．如图所示，在倾角为θ＝37°的斜面底端的正上方H高处水平抛出一物体，空气阻力不计，该物体落在斜面上时的速度方向正好与斜面垂直，则物体抛出时的初速度大小v₀为_________。

【答案】

\(\frac{{\sqrt {153gH} }}{{17}}\)

 

84．甲球在地面，乙球在甲球正上方h高处，甲球以初速v₀作竖直上抛运动，同时乙球作自由落体运动，则它们能在空中相遇的条件是______，它们在甲上升过程中相遇的条件是_______。

【答案】

v₀²＞\(\frac{{gh}}{2}\)，v₀²＞gh

 

85．如图所示，一长为L的杆，下端铰于地面，上端固定一个小球，杆搁在一边长为a的正方体上，正方体以速度v向右匀速运动，则当滑到杆与水平面成α角时，杆与正方体的接触点沿杆滑动的速度大小为______，杆转动的角速度为______，小球的运动速度大小为______。

【答案】

vcosα，\(\frac{{v{{\sin }^2}\alpha }}{a}\)，\(\frac{{vL{{\sin }^2}\alpha }}{a}\)

 

86．从高为H的A点平抛出一个物体，其水平射程为2s，在A点的正上方距A点为H的B点，同方向平抛另一物体，其水平射程为s，两物体在空中的运行轨道在同一竖直平面内，且都从同一竖直屏的顶端C点擦过，求C点的高度。

【答案】

\(\frac{6}{7}\)H

 

87．在地面上以20 m/s的初速竖直上抛一物体，空气阻力不计。该物体在1 s内两次通过电线杆的顶端，此电线杆的高度是________。

【答案】

18.75 m

 

88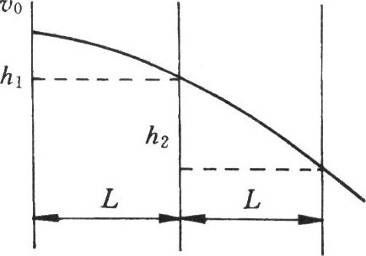．如图所示，为测定一玩具枪射出的子弹的初速度，将枪管水平固定后，在枪正前方垂直于枪管放置三个薄纸屏，相邻纸屏间的距离都为L＝0.4 m，子弹穿过纸后留下三个弹孔，相邻两个弹孔的高度差分别为h₁＝0.4 m，h₂＝0.8 m，试计算子弹的初速度大小。

【答案】

2 m/s

 

89．在足够高处以初速度20 m/s竖直上抛一物体，空气阻力不计，第1 s末到第5 s末物体通过的路程为____m。

【答案】

50

 

90．将一物体竖直向上抛出，空气阻力不计，经时间t回到出发点，则物体到达最大高度一半处时的速度大小为______。

【答案】

\(\frac{{\sqrt 2 gt}}{4}\)

 

91．自动扶梯60 s可将站在扶梯上相对扶梯不动的人送上楼，人如果沿着开动的自动扶梯走上楼，需时45 s，则人如果沿着不动的自动扶梯走上楼需时______s。

【答案】

180

 

92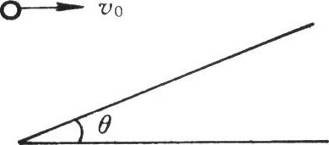．如图所示，以水平初速v₀＝10 m/s抛出一物，空气阻力不计，恰好垂直于倾角θ＝30°的斜面撞到斜面上，则从抛出到达斜面所经历时间为______s。

【答案】

\(\sqrt 3 \)

 

93．甲、乙两个物体在同一高度分别以初速度为v₀、3v₀同时水平抛出，空气阻力不计，经过时间t后，甲、乙两个物体下降的高度之比是____，所通过的水平距离之比是_____。

【答案】

1∶1，1∶3

 

94．一架飞机以200 m/s的速度水平匀速飞行，飞机上有一人，每隔2 s放下一个物体，空气阻力不计。当第6个物体离开飞机时第1个物体刚好着地，此时第3个物体与地面间的距离是______m。

【答案】

80

 

95．从地面竖直上抛的小球，空气阻力不计，在抛出后的时刻t₁和时刻t₂的位移相同，则它抛出时的初速度大小为_________，在时刻t₁时离地面的高度为________。

【答案】

\(\frac{1}{2}\)g（t₁＋t₂），\(\frac{1}{2}\)gt₁t₂

 

96．以20 m/s速度竖直上抛一小球，空气阻力不计，从抛出时开始计时，当小球位移为向上10 m时，与之对应的时间可能是（    ）

（A）(2-\(\sqrt 2 \))s             （B）(2+\(\sqrt 2 \))s            （C）(2-\(\sqrt 6 \))s             （D）(2+\(\sqrt 6 \))s

【答案】

AB

 

97．对于由两个分运动合成的运动，正确说法是（      ）

（A）合运动速度一定大于两个分运动的速度

（B）合运动方向就是物体真实运动的方向

（C）由两个分速度的大小可以确定合速度的大小

（D）两个直线运动的合运动也可能是曲线运动

【答案】

BD

 

98．船在水速为口的河上摆渡，则下列说法中正确的是（     ）

（A）船头垂直河岸航行到达对岸所需时间最小

（B）船头垂直河岸航行实际航程最短

（C）要实际航程最短必须使船头朝上游转过一定角度

（D）要到达对岸时间最短必须使船头朝上游转过一定角度

【答案】

AC

 

99．一船在静水中以速度v₁，往返于沿河流方向的甲、乙两地需时间t₁，若水流速度为v₂，船仍以速度v₁，往返于甲、乙两地需时间t₂，则t₂等于 （    ）

（A）\(\frac{{{v_1}}}{{{v_1} - {v_2}}}\)t₁              （B）\(\sqrt {\frac{{v_1^2}}{{v_1^2 - v_2^2}}} \)t₁              （C）\(\frac{{v_2^2}}{{v_1^2 - v_2^2}}\)t₁              （D）\(\frac{{v_1^2}}{{v_1^2 - v_2^2}}\)t₁

【答案】

D

 

100．关于平抛运动在空中飞行的时间T，正确的说法有（     ）

（A）初速越大T也越大                          （B）抛出点离地越高T也越大

（C）T与水平射程和抛出点高度均有关  （D）T与同高度自由落体时间相同

【答案】

BD

 

101．将一物从高h处以初速v₀水平抛出，空气阻力不计，水平射程为s，落地速度大小为v₁，则飞行时间为（    ）

（A）\(\sqrt {\frac{{2h}}{g}} \)        （B）\(\frac{{\sqrt {v_1^2 - v_0^2} }}{g}\)          （C）\(\frac{s}{{{v_1}}}\)       （D）\(\frac{{2h{v_0}}}{{gs}}\)

【答案】

ABD

 

102．水平匀速飞行的飞机上，每隔相等时间落下一个小球，不计空气阻力，每个小球的运动轨迹及这些小球在空中的连线分别是（    ）

（A）抛物线，倾斜直线            （B）竖直直线，倾斜直线

（C）抛物线，竖直直线            （D）竖直直线，折线

【答案】

C

 

103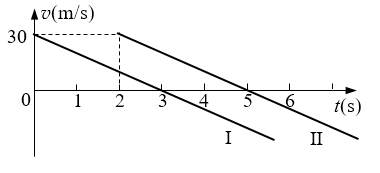．如图所示，图线I和Ⅱ分别表示先后从同一地点以相同速度v作竖直上抛运动的两物体的v-t图线，则两物体（     ）

（A）在第Ⅰ个物体抛出后3 s末相遇

（B）在第Ⅱ个物体抛出后4 s末相遇

（C）在第Ⅱ个物体抛出后2 s末相遇

（D）相遇时必有一个物体速度为零

【答案】

C

 

104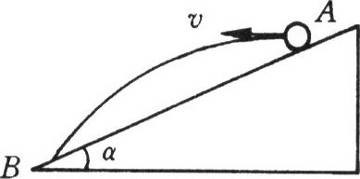．如图所示，在倾角α的斜面上A点，以速度v水平抛出一小球，空气阻力不计，落在斜面上的B点。求：

（1）AB的距离；

（2）球到B点时的速度大小。

【答案】

（1）\(\frac{{2{v^2}\sin \alpha }}{{g{{\cos }^2}\alpha }}\)

（2）v\(\sqrt {1 + 4{{\tan }^2}\alpha } \)

 

105．离地面高度为1470 m处，一架飞机以360 km/h的速度水平飞行，已知由飞机上自由落下的物体在离开飞机10 s后因降落伞张开而作匀速运动，为使物体投到地面上某处，应该在离开该地水平距离多远处开始投下该物体（设水平方向运动不受降落伞的影响）？

【答案】

1970 m

 

106．一石子自塔顶竖直上抛，空气阻力不计，回落时，经过塔顶下h处的速度是经过塔顶上h处速度的2倍，则上抛的初速是______。

【答案】

\(\sqrt {\frac{{10gh}}{3}} \)

 

107．以v₀＝10 m/s的速度匀速上升的气球，当上升到离地高为20 m处时落下一小物体，空气阻力不计，该物体从离开气球到着地所需时间t＝______s，着地时的速度大小为______m/s。

【答案】

3.24，22.4

 

108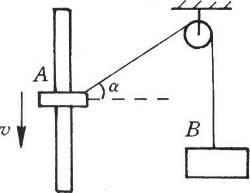．如图所示，A、B两物体用跨过滑轮的细绳相连，A物体又套在竖直杆上，当使A物体以速度v匀速下滑时，物体B的运动速度将（填“增大”、“不变”或“减小”），运动到细绳与水平方向成α角时，B物体的速度大小为______。

【答案】

增大，vsinα

 

109．把小球水平抛出，空气阻力不计，抛出后在t₁、t₂、t₃三个时刻，小球的速度与水平方向的夹角分别是30°、45°、60°，则t₁∶t₂∶t₃＝______，小球自抛出到此三个时刻下落的高度之比h₁∶h₂∶h₃＝______。

 

【答案】

1∶\(\sqrt 3 \)∶3，1∶3∶9

 

110．水平抛出一小球，空气阻力不计，t s末的速度与水平成45°角，（t＋1）s末与水平成60°角，可知小球抛出时的速度大小是______。

【答案】

\(\frac{g}{{\sqrt 3  - 1}}\)（提示∶抓住两个分运动的速度关系）

 

111．在某点以速度v₀竖直向上抛出物体A后，又以\(\frac{{{v_0}}}{3}\)的速度竖直向上抛出物体B，空气阻力不计，要使两物体能在空中相遇，那么先后抛出两物体的时间间隔Δt应满足的条件是______。

【答案】

\(\frac{{2{v_0}}}{g}\)＞Δt＞\(\frac{{4{v_0}}}{{3g}}\)（提示∶可用位移-时间图分析）

 

112．一人划船横渡一条河，在静水中划船速度v₁和水流速度v₂大小一定，且v₁＞v₂，但均未知，此船渡河的最少时间为T₁，若此船用最短的位移过河所需时间为T₂，则划船速度与水流速度之比v₁∶v₂＝_________。

【答案】

\(\frac{{{T_2}}}{{\sqrt {T_2^2 - T_1^2} }}\)

 

113．将甲球竖直上抛，同时将乙球竖直下抛，两球初速度大小相等，抛出高度相同，空气阻力不计，则（   ）

（A）落地时的速度甲较大                      （B）落地所需时间甲较大

（C）整个过程中平均速度相同               （D）整个过程的速度改变量相同

【答案】

B

 

114．关于运动合成，下列说法中正确的是（    ）

（A）两个直线运动的合运动一定是直线运动

（B）两个互成角度的匀速直线运动的合运动一定是匀速直线运动

（C）两个互成角度的匀变速直线运动的合运动一定是匀变速直线运动

（D）两个分运动的运动时间一定等于它们合运动的时间

【答案】

BD

 

115．从地面竖直上抛物体A，与此同时B在高处自由下落，空气阻力不计，它们在空中相遇时，速度大小都为v，则（    ）

（A）A上抛的初速为2v

（B）A上升的高度与B下落的高度相同

（C）A，B落地所需时间相同

（D）A，B落地时速度相同

【答案】

ABD

【解析】

提示∶可利用图线法分析

 

116．一小球从地面竖直上抛，落地后弹起又落下，空气阻力不计，图中能正确表示它的速度与时间关系的是（    ）

【答案】

A

 

117．在同一竖直线上不同高度的a、b两点（a在上方），分别以v₁和v₂的速度同时水平抛出两个小球，不计空气阻力，下列说法正确的是（     ）

（A）只有v₁＝v₂时，两球才能在空中相遇

（B）只有v₁＞v₂时，两球才能在空中相遇

（C）只有v₁＜v₂时，两球才能在空中相遇

（D）不管v₁和v₂关系如何，两球在空中不可能相遇

【答案】

D（提示：竖直方向在相同时间内下落高度相同，因而两物体总有高度差）

 

118．水平抛出一个小球，抛出时速度为v₀，落地时速度为v₁，忽略空气阻力，图中能够正确地表示在三段相等时间内速度矢量的变化情况的是（    ）

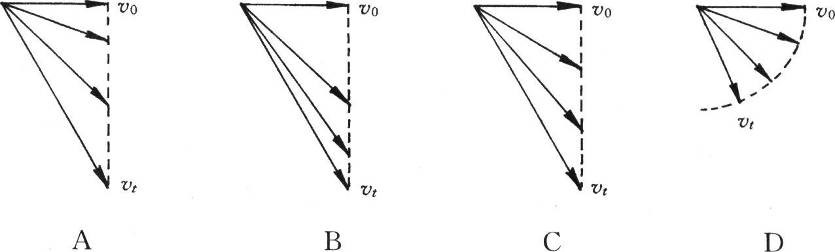
【答案】

C（提示：竖直方向分运动的速度是均匀增大的）

 

119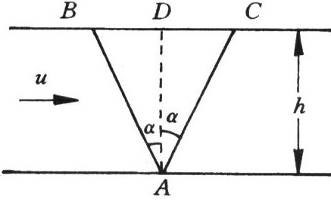． 如图所示，河宽为h，水流流速恒定为u，小船在静水中的速度为v。今令小船自A点出发渡河，第一次小船以AB航线渡河，第二次小船沿AC航线渡河，已知AB、AC与河岸垂线间的夹角都为α，则两次渡河所需时间相比（              ）

（A）沿AB航线较长                （B）沿AC航线较长

（C）两航线相等                      （D）无法比较

【答案】

A（提示：要沿AB航线行驶，其静水中的船速方向与河岸的夹角较小，因而其垂直河岸的分速度也较小）

 

120．以初速v₀相隔Δt时间先后从同一高度竖直上抛a、b两物体，空气阻力不计，当它们在空中相遇时（    ）

（A）两物体速度完全相同                                    （B）a的速度值比b大

（C）a的加速度向下，b的加速度向上                  （D）两物体加速度完全相同

【答案】

D

 

121．地面竖直上抛一物体，空气阻力不计。通过楼上1.5 m高的窗口历时为0.1 s。物体回落时，从窗口底到地面时间为0.2 s，求物体能到达的最大高度。

【答案】

15.3 m

 

122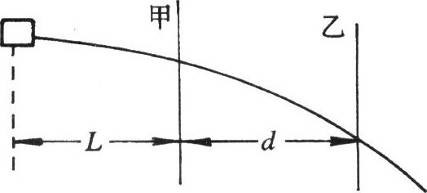． 如图所示，一玩具手枪水平射出一颗子弹，在离枪口L处竖直放一薄纸屏甲，在甲后相距d处再竖直放一薄纸屏乙，子弹在纸屏上留下两个弹孔，两弹孔高度差为h，求子弹的初速度。

【答案】

\(\sqrt {\frac{{(2L + d)dg}}{{2h}}} \)（提示：水平方向有L＝v₀t₁，L+d＝v₀t₂，竖直方向有2gh＝v₂²－v₁²）

 

123．从离地面高h处以水平速度v₀抛出一物体A，在Δt时间后又在地面上某处以足够大的初速v₀′竖直上抛一物体B，空气阻力不计，问当符合什么条件时，两物体才能在空中相碰。

【答案】

（1）轨迹在同一竖直平面内，A的初速指向B所在一面

（2）A、B水平距离d＜v₀\(\sqrt {\frac{{2h}}{g}} \)

（3）A、B抛出的时间差Δt=\(\frac{d}{{{v_0}}} - (\frac{{{v_0}}}{g} \pm \sqrt {\frac{{v_0^2}}{g} - \frac{{2h}}{g} + \frac{{{d^2}}}{{v_0^2}}} )\)（提示：有两解是可能在B上升时相遇，也可能在B下降时相遇，且当d/v₀＝h/v₀′时Δt＝0）？？？