1．一辆速度为16m/s的汽车，从某时刻开始刹车，在制动阻力的作用下，以2m/s²的加速度做匀减速直线运动。问经过10s后汽车离开刹车点多远 ？

【答案】

64m

【解析】

【分析】汽车从刹车起做匀减速直线运动直到停下，所经历的时间有可能小于10s，因此不能直接利用位移公式计算，正确的做法是，先算出汽车从刹车到停下所经历的时间，将结果与题中所给的时间比较，再确定减速过程中汽车的位移。

【解答】已知初速度v₀＝16m/s、末速度v＝0、加速度a＝2m/s²，由速度公式

v＝v₀＋at，

可得

t＝\(\frac{{{v_t} - {v_0}}}{a}\)＝\(\frac{{0 - 16}}{{ - 2}}\)s＝8s。

由于汽车从刹车到停下所经历的时间仅为8s，所以经过10s后汽车离开刹车点的距离为

s＝v₀t＋\(\frac{1}{2}\)at²＝[16×8＋\(\frac{1}{2}\)×（－2）×8²]m＝64m。

作为比较，如果将t＝10s直接代入上式，得s＝60m，这个结果显然是错误的。

 

2．物体做匀变速直线运动，加速度为2m/s²，若在开始10s内前进了5m，那么随后的10s内该物体前进几米 ？

【答案】

205m

【解析】

【分析】将所讨论的运动过程分为两段：（1）第一段：已知加速度a＝2m/s²、时间t＝10s、位移s₁＝5m，而初速度v₀和末速度v₁未知；（2）第二段：已知加速度a＝2m/s²、时间t＝10s，初速度就是第一段运动过程的末速度v₁，而位移s₂和末速度v₂未知。

【解答】由第一段运动过程的位移公式s₁＝v₀t＋\(\frac{1}{2}\)at²可得，第一段运动物体的初速度为

v₀＝\(\frac{{{s_1} - \frac{1}{2}a{t^2}}}{t}\)＝\(\frac{{5 - 0.5 \times 2 \times {{10}^2}}}{{10}}\)m/s＝－9.5m/s

上式中，我们取加速度a的方向为正方向，v₀为负，这表示开始有一段运动是沿相反方向的匀减速运动，当速度减小到0后，物体再做匀加速运动。

第一段运动过程的末速度为

v₁＝v₀＋at＝（－9.5＋2×10）m/s＝10.5m/s。

再由第二段的位移公式，可得随后10s内物体前进的路程：

s₂＝v₁t＋\(\frac{1}{2}\)at²＝（10.5×10＋0.5×2×10²）m＝205m。

【讨论】本题有多种解法，其中最简单的一种是直接利用推论：s₂－s₁＝aT²。不过，在初学阶段，学会用最基本的公式求解问题是非常重要的。通过基本公式求解还能对所讨论的运动过程获得全面而清晰的认识。

 

3．一辆汽车做匀加速直线运动，初速度v₀＝4m/s，加速度a＝2m/s²。

（1）求t＝1、2、3、…、10s时刻该物体的速度和位移；

（2）作出该车10s内的v-t图和s-t图。

【答案】

略

 

4．右图是一辆汽车做直线运动时的v-t图，汽车的初速度是______；最大速度是______；末速度是_______，它从t＝到t＝10s间，做______运动，加速度是_____，经过的路程是______；从t＝10s到t＝40s之间，做______运动，经过的路程是____；从t＝40s到t＝50s，做_____运动，加速度是______，经过的路程是______。

【答案】

5m/s；10m/s；0；初速不为零的匀加速直线；0.5m/s²；75m；匀速直线；300m；匀减速直线；－1m/s²；50m

【解析】

无

 

5．一辆赛车，在4s时间内，它的速度由4m/s均匀增加到36m/s，它的加速度多大？行驶了多少距离？

【答案】

8m/s²；80m

【解析】

无

 

6．一架超音速喷气式飞机从145m/s的速度开始加速飞行了20s，加速度为23.1m/s²。求它的末速度，以及这段加速过程中飞行的距离。

【答案】

607m/s；7520m

【解析】

无

 

7．汽车行驶速度从10m/s均匀增加到20m/s，行驶的距离为75m。求汽车的加速度和这段加速行驶的时间。

 

【答案】

2m/s²；5s

 

8．右图是一张飞机即将降落时的照片。飞机着落后在跑道上的滑行过程，可近似看作匀减速直线运动过程，设跑道长3km，飞机落地时的速度为120m/s。问：飞机滑行时的加速度应至少多大？

【答案】

－2.4m/s²

【解析】

无

 

9．汽车性能的一个重要指标是，使它的车速从0增加到100km/h所需时间T。现有某型号的跑车，T＝5.2s。问：这辆跑车以最高的加速度使它的时速从72km/h增加到180km/h的过程中，行驶了多少距离？需多少时间？

 

【答案】

196.6m；5.62s

 

10．列车在开始制动后，经20s停止，这段时间内列车的位移是120m。求列车开始制动时的速度和它的加速度。

【答案】

12m/s；－0.6m/s²

【解析】

无

 

11．图中表示四个小球向右运动过程的闪光摄影照片，闪光时间间隔为0.05s。

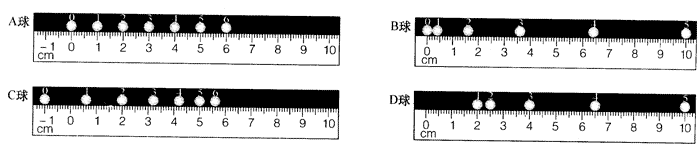
（1）指出这些小球的运动特点，是匀速直线运动，还是匀变速或非匀变速直线运动？

（2）如果是匀速或匀变速运动，则进一步指出描写这些运动的物理量（如速度、加速度、初速度等）。

 

【答案】

A球做匀速直线运动，速度v＝－0.2m/s；B球做初速为零的匀加速直线运动，加速度a＝－3.2m/s²；C球做匀减速直线运动，初速度v₀＝0.34m/s，加速度a＝－0.8m/s²；D球做初速为零的匀加速直线运动，加速度a＝4m/s²。对于变速运动，求解该题的基本方法是，对每个小球取任意两组位移和时间数据：（s₁，t₁）、（s₂，t₂），代入位移公式，解出初速度和加速度，然后取第三组数据加以验证。

【解析】

无

 

12．王先生驾驶一辆汽车，以108km/h的速度在高速公路上行驶，与前方汽车的车距为80m。这时，王先生看到前方那辆汽车突然刹车，他立即在0.8s后也采取了刹车措施，使他的汽车以数值为6m/s²的加速度做减速运动。如果前方汽车刹车后需向前滑行20m方能停下。问：王先生的这辆汽车会撞上前方那辆车吗？

 

【答案】

不会，但此时两车仅相距1m，非常危险

 

13．某段高速公路上容许的最高车速为144km/h。假定驾驶员的“反应时间”为0.8s，刹车时的加速度为－5.4m/s²。试求该车应保持的“安全距离 ”。

 

【答案】

大于180.2m

 

14．交通警察在路边某处发现了一辆违章卡车，当这辆卡车以6m/s的速度驶过该处时，突然以1.2m/s²的加速度加速前进，企图逃逸。与此同时，警察则立即驾驶摩托车以2m/s²的加速度追赶卡车，卡车和警用摩托车的最高时速分别为54km/h和72km/h。问：警察要多久才能追上卡车？追上时，摩托车行驶了多长路程？

 

【答案】

13.25s；165m

 

15．（1）一辆正在上坡的汽车熄火后沿山坡下滑，当下滑速度为3m/s时，发动机启动了，经2.5s后，汽车又以4.5m/s的速度继续上坡，取上山方向为正方向，则汽车的加速度为多大 ？

（2）画出（1）中这辆汽车的v-t图，然后利用v-t图求它的加速度。

【答案】

（1）a＝3m/s²，方向指向上坡方向

（2）略

 

16．假设航空母舰的甲板跑道长238m，舰载飞机降落时的速度为60m/s，制动加速度为-5m/s²。问：这种情况能否降落？实际舰载飞机降落过程中还要利用阻力伞装置，以增强减速作用。设飞机降落后经过3s，阻力伞才打开。问：为了安全降落，阻力伞打开后，飞机的制动加速度至少应多大？

 

【答案】

不能，12.58m/s²

 

17．汽车以36 km/h的速度匀速行驶，如果以1.6m/s²的加速度使它的速度均匀地增加一倍，需多少时间？

 

【答案】

6.25 s

【解析】

无

 

18．李先生驾驶一辆小汽车，以90km/h的速度在高速公路上行驶，并小心地与前方汽车保持60m车距。不巧，由于前方那辆汽车突然刹车，李先生的车一头撞了上去，发生了追尾事故。交警赶来调查处理时，他争辩说：“按照国家标准，我的轿车的制动距离只要20m，而我则保持了60m车距，因此对这次事故我没有责任。”你的看法呢？

【答案】

李先生没有正确理解上表中数据的含义。这里，首先要从机动车“制动距离”国家标准的相应数据，推算出他的汽车制动时能达到的最大加速度。根据上表数据，他的汽车在初速度v₀＝50km/h＝13.9m/s时的制动距离为20m，所以该车制动时的加速度可利用速度与位移关系式v²－v₀²＝2as求得

a＝－4.83m/s²。

现在轿车的初速度v₀ʹ＝90km/h＝25m/s；末速度vʹ＝0；加速度a＝－4.83m/s²。因此制动距离是

sʹ＝64.7m。

即李先生的这辆车此时与前方汽车的距离应至少等于64.7m。

 

19．一辆警车在高速公路上以36km/h的速度行驶，此时接到命令，在前方4km处发生车祸，该警车于是立即加速向事故发生地驶去。设警车加速或减速时加速度的值都是2.8m/s²，最高时速为180km/h。试估计这辆警车赶到事故发生地所需最短时间。

 

【答案】

94.7s

 

20．将蹦床运动抽象为竖直上抛运动。运动员为了达到8 m的高度，弹跳后刚脱离蹦床时的速度应多大？跳起后达到最大高度需多少时间？（取g＝10 m/s² ）

【答案】

12.6 m/s，1.26 s

 

21．气球常用于科学探测和观光旅游。如图所示，在高度 100 m 处有两只气球（气球甲和气球乙），以相同速度 5 m/s 分别匀速上升和匀速下降，此时，在这两只气球上各掉出一物体，问：这两个物体落到地面时它们的速度差、时间差，以及所经过的路程差各是多少？（取 g ＝ 10 m/s²）

【答案】

Δs＝s_A－s_B＝2.5 m，

Δv＝v_A－v_B＝0，

Δt＝t_A－t_B＝1 s。

 

22．气球以v₀＝10m/s的速度匀速上升。当到达离地面高h＝175 m处时，从气球下面的吊篮中掉落一重物。求该重物落到地面所需时间。（g＝10 m/s²）

 

【答案】

t＝7 s

 

23．一个物体竖直上抛，到达最高点后再自由落下，在这过程中，物体的速度如何变化？加速度如何变化？位移如何变化？路程如何变化？

 

【答案】

速度先减小后增加，a不变，位移先增加后减小，路程一直增加

 

24．信号弹以100 m/s的速度竖直向上射出，在最初2 s内它上升多高？可能达到的最大高度是多少？多少时间落回原地？（g＝10 m/s²）

 

【答案】

180 m；500 m；20 s

 

25．为了估测某一大楼的高度，某人从地面上用力竖直向上抛出一块小石块，使它大约达到大楼的高度，并测得该石块从地面上抛出到落回地面的时间为4 s，试估计该大楼的高度。（g＝10 m/s²）

 

【答案】

20 m

 

26．从地面竖直上抛的物体在下落阶段的平均速度是12m/s，求它的上升高度。（g＝10 m/s²）

【答案】

28.8 m

 

27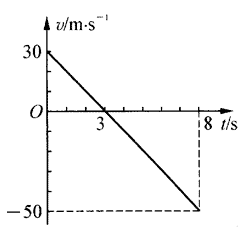．竖直上抛物体经8 s后落地，它的v-t图如图所示。从这图上，你能“读出”该物体运动过程中的哪些信息？写出它的速度和位移随时间变化的函数关系。

【答案】

由图可知，以竖直向上方向为正方向，该物体上抛时的初速度为30 m/s，落地时的末速度为－50 m/s，加速度为－10 m/s²，上抛3 s后到达最高点，从最高点落到地面需时5 s，物体上升的最大高度在抛出点上方45 m处，落地点在抛出点下方80 m处；速度和位移随时间变化的函数关系分别是：v＝30－10t，s＝30t－5t²

 

28．直升飞机现已广泛应用于突发性灾难的救援工作。从一架离地面高度为60 m，且正在以3 m/s的速度下降的直升飞机上落下一包救援物资。这包物资落到地面需多少时间？速度多大？（g＝10 m/s²）

 

【答案】

3.18 s；34.8 m/s

 

29．以20 m/s的初速度从地面竖直上抛一物体，该物体两次经过电线杆的顶端的时间间隔为3 s，求电线杆的高度。（g＝10 m/s²）

【答案】

8.75 m

 

30．一个做竖直上抛运动的物体，上升过程中的平均速度为10 m/s，它能达到的最大高度是多少？（g＝10 m/s²）

 

【答案】

20 m

 

31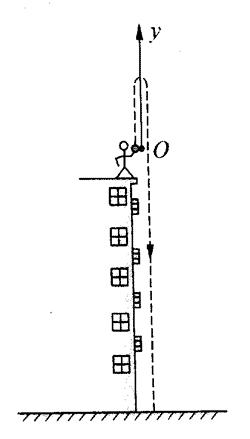．从高楼上以20 m/s的初速度竖直向上抛出一物体（如图所示）。问：在1 s、4 s、5 s末该物体的位移及路程各是多少？（g＝10 m/s²）

【答案】

位移分别是15 m、0、－25 m；路程分别是15 m、40 m、65 m（取抛出点为坐标原点，竖直向上方向为坐标轴的正方向）

 

32．甲乙两物体分别自高度为45 m和60 m处做初速为零的自由落体运动和初速不为零的下抛运动，但同时到达地面。问甲物体的末速度和乙物体的初速度及末速度各是多少？（g＝10m/s²）

【答案】

30 m/s；5 m/s；35 m/s

 

33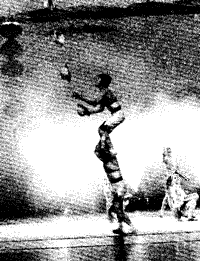．类似图中的杂技表演，假设杂技演员依次竖直向上抛出4个小球，每个小球上升的最大高度均为1.25 m。假定该演员抛出一个球后立即接到另一个球，使空中总有三个球，手中留有一个球。求：每个球在演员手中停留的时间。

【答案】

\(\frac{1}{3}\) s

 

34．一个物体做竖直上抛运动，途中经过一扇高度为2 m的窗户，历时0.21 s。试求物体上升的最高点与窗户上边框的距离。（g＝10 m/s² ）

 

【答案】

3.59 m

 

35．从某一高度处分别以相同的速率竖直上抛和竖直下抛两物体，这两个物体由抛出到落地所需时间分别是8 s和1 s。求抛出时物体的速率和高度。（g＝10 m/s²）

 

【答案】

35 m/s；40 m