关于功的定义的一点意见

关于功的定义，各种课本的说法不同。原高中物理课本是这样说的；“功的大小等于力和受力作用的物体在力的方向上所通过的路程的乘积。如果用 F 代表力，用 s 代表物体在力的方向上通过的距离，用W代表力所做的功，那么 W＝Fs”新编高中物理课本没有给出功的完整表述，初中课本的说法与此相同。一般普通物理的说法是：“功的数值等于力 F、力的作用点的位移 s 及力与位移的方向间的夹角的余弦的乘积，即 W＝Fscosθ。”总的来说，功的各种叙述的主要区别在于：有的用“物体的位移”（原高中课本用距离，严格来说应是位移，对作单向的直线运动的质点来说，它的位移数值和路程相等），有的用“力的作用点的位移”。一般来说，物体的位移和力的作用点的位移是有区别的。通过下面的例子分析，我们将看到：用力和物体的位移的乘积来定义功是不恰当的；用力和力的作用点的位移的乘积来定义功才符合实际。

例如，一质量为 m，半径为 R 的匀质圆盘平放在光滑的水平面上，盘面也绝对光滑。若在圆盘的边上作用一个力 F，设力 F 的作用线通过圆盘质心C（见图1）。

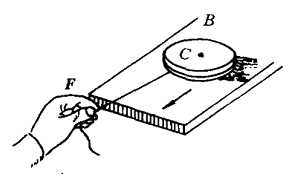
当圆盘在力F的作用下移动 s 时（所经历时间为 t），F 所做的功 W＝Fs。将 s＝at²/2，F＝ma（质心运动定律）分别代入功的表达式则得：

 W＝mv_C²/2

这里 v_C＝a_Ct 为质心 C 在 t 时刻的速度大小。现以相同的力F作用在圆盘的边缘切向上（用一忽略质量的细线绕在盘的边缘上，用力 F 拉线），如图2所示，并使圆盘同样移动s（可证所经历时间仍是 t），此时，如按“物体的位移”来计算功，则F所做的功仍是 W＝mv_C²/2 。其实，由于力F未通过盘质心C，圆盘既有平动又有绕质心C的转动，作为圆盘的力的瞬时作用点，除参与质心的平动外，还要参与绕质心的转动，因而力的作用点的位移应是质心的位移和力的瞬时作用点绕质心转动的位移之和。

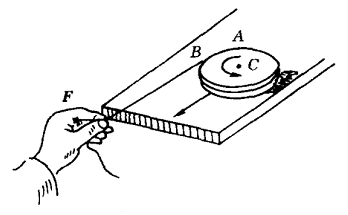
在dt时间内，上述两位移分别为：

s_平动＝v_Cdt

s_转动＝Rωdt

且方向一致。所以作用点的合位移为：

s_总＝s_平动＋s_转动＝v_Cdt＋Rωdt

如按力的作用点的位移来计算功，则在dt时间内力F所做的功为dW＝F（v_Cdt＋Rωdt）。因为F是恒力，所以圆盘质心作匀加速运动，转动也是匀角加速的。于是，在质心移动s的有限时间t内，力F所做的总功为：

\[\begin{array}{*{20}{l}}{W = \int_0^t {F({v_C}dt + R\omega dt)} }\\{ = F\left[ {\int_0^t {{a_C}dt + R\int_0^t {{\beta _C}tdt} } } \right]}\\{ = F\left[ {\frac{1}{2}{a_C}{t^2} + R\frac{1}{2}{\beta _C}{t^2}} \right]}\\{ = \frac{1}{2}ma_C^2{t^2} + ma_C^2{t^2}}\\{ = \frac{3}{2}ma_C^2{t^2}}\\{ = \frac{3}{2}mv_C^2}\end{array}\]

其中用到质心运动定律F＝ma_C，转动定律FR＝（mR²/2）β_C。

显然，在这里，按照“物体的位移”算得的功与按照“力的作用点的位移”算得的功是不同的。何种正确？就须进一步验证。

下面就根据动能定理来验证。

如上所述，在边缘恒力F作用下，匀质圆盘既有质心的平动又有绕质心的转动。设F作用时间为t，则到t时刻圆盘就有确定的运动状态，从而就有着确定的动能，根据动能定理，此时圆盘的动能值就应等于t时间内恒力F所做的功值。圆盘的平动动能：

E_平动＝mv_C2/2＝ma_C²t²/2 （1）

圆盘的转动动能：

E_转动＝ I_Cω_C²/2 （2）

\({{\rm{I}}_{\rm{C}}} = \frac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)，I为圆盘对通过质心的垂直轴的转动惯量，ωC为圆盘在t时刻绕质心的转动角速度。因为：

ω_C＝β_Ct

F＝ma_C

FR＝I_Cβ_C

β_C是盘绕质心转动的角加速度。因为：

\({\beta _{\rm{C}}}{\rm{ = }}\frac{{FR}}{{{I_C}}} = \frac{{2{a_C}}}{R}\)

于是：

ω_C＝2a_Ct/R

代入（2）式得：

E_转动＝ma_C²t²

最后得圆盘t时刻的总动能为：

E_动＝E_平动＋E_转动＝\( \frac{3}{2}{\rm{m}}{{\rm{a}}_{\rm{C}}}^{\rm{2}}{{\rm{t}}^{\rm{2}}} = \frac{3}{2}{\rm{m}}{{\rm{v}}_{\rm{C}}}^{\rm{2}}\)

与上述按“力的作用点位移”算得的功值相等，故按“力的作用点的位移”计算功值是符合动能定理的，正确的。事实上，作用在圆盘边缘的切向恒力 F 在时间 t 内所做的功一部分用来增加盘的平动动能mv_C²/2，另一部分是用来增加盘的转动动能 mv_C² 的。显然，如果仅考虑盘的质心位移，而不从力的作用点的位移来考虑是得不到正确结果的。

上述的例子只是指物体的转动情况，事实上，即使对于没有转动的物体，有时也必须从“力的作用点的位移”来计算功，才能得出正确的结果。如图3所示，用一质量不计的弹性系数为k的弹簧连接一重物 M。若用力 F 将弹簧拉长 x，但重物因受阻力作用未动。在此问题中，若按“物体的位移“来算功，由于物体位移为零，则力 F 所做功为零，显然是错误的。只有从“力的作用点的位移”来计算功才能得到 \(\int_0^{\rm{x}}{{\rm{kxdx = }}\frac{1}{2}{\rm{k}}{{\rm{x}}^2}} \) 这个正确的结果。

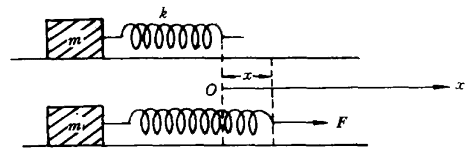
由以上分析可知，功的定义应为：力和力的作用点在力的方向上通过的位移的乘积。现行课本中用了物体移动的位移（初中是路程），用“路程”，这对初中学生来说，是比较容易接受的，也是可取的。但是，在高中物理中应指出是“力的作用点的位移”。

发布时间：2012/6/13 上午9:45:20  阅读次数：9357