1.2 符号和定义
本节将对本书中涉及的一些数学符号进行说明,关于本书中用到的名词的详细解释可参见附录A。
1.2.1 数学符号
表1.1总结本书用到的的大部分数学符号,这里对其中的部分概念进行详细解释。
| 类型 | 符号表示 | 示例 |
|---|---|---|
| 角度 | 小写希腊字母 | αi,φ,η,ρ,γ242,θ |
| 标量 | 小写斜体 | a,b,t,uk,v,wij |
| 向量或者点 | 小写粗体 | a,u,vs,h(ρ),hz |
| 矩阵 | 大写粗体 | T(t),X,Rx(ρ) |
| 平面 | π:向量+标量 | π:n•x+d=0, π1:n1•x+d1=0 |
| 三角形 | △三个点 | △v0v1v2,△cba |
| 线段 | 两个点 | uv,aibj |
| 几何实体 | 大写斜体 | AOBB,T,BAABB |
角度和标量均属于实数集R,也就是说,它们都是实数。向量和点用黑体小写字母表示,相关分量可以用下列形式存取。
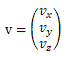 (1.1)
(1.1)
即这是一种列向量形式,目前在计算机图形学界普遍采用这种表示形式。在本书很多地方,常常使用(vx,vy、vz),而不是(vx vy vz)T形式,这是因为前者的可读性要好一些。
在齐次坐标系中(参见附录A.4节)。坐标可以用(vx vy vz vw)T表示。其中一个向量是v=(vx vy vz 0)T,一个点是v=(vx vy vz 1)T。有时候只使用具有3个元素的向量和点。但是尽可能避免出现表示类型上的歧义。对于矩阵操作来说,向量和点最好使用同一种符号表示形式(关于变换操作可参见第4章,关于齐次符号表示可参见附录A.4节)。在一些算法中,使用数字索引要比使用x、y、z更方便,如v=(v0 v1 v2)T。对于两个元素的向量来说,关于向量和点的所有这些规则依然成立,只是忽略了三元向量中的第3个分量而已。
关于矩阵.需要多一些解释,最常使用的矩阵大小是2×2、3×3、4×4。这里,通过回顾一下3×3矩阵M的相关操作,就很容易将这种操作过程扩展到其他大小的矩阵。矩阵M的(标量)元素可以用mij表示,其中0≤(i,j)≤2,i表示行,j表示列,具体表示参见式(1.2)。
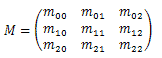 (1.2)
(1.2)
式(1.3)中所示的关于3×3矩阵的符号表示,可以将向量和矩阵M区分开:mj表示第j个列向量,mi表示第i个行向量(以列向量形式表示)。对于向量和点来说,也可以用x、y、z或w来索引列向量,条件是这种表示方式更方便。
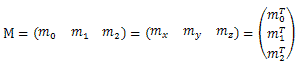 (1.3)
(1.3)
平面可以用π:n•x+d=0来表示,同时也是它的数学公式,包含了平面法线n和标量d,法线是表示平面朝向的一个向量,更通用的说法是(例如对于一个曲面)法线表示的是平面上一个特定点的方向,对于平面来说,所有点的法线都是相同的。π是平面表示的的常用数学符号。可以认为平面π将空间分为正半空间(其中n•x+d>0)和负半空间(其中n•x+d<0),其他所有点都位于平面上。
三角形可以用三个点v0、v1、v2来定义,用△v0v1v2来表示。
表1.2给出了其他的一些数学操作符及相应的符号表示,关于点乘、叉乘、行列式、长度等操作符参见附录A。转置操作符将一个列向量转换为一个行向量反之亦然。这样可以将列向量写成一种压缩形式如(vx vy vz)T。关于第4个操作符,需要进一步解释:u⊗v表示向量(uxvx uyvy uzvz)T,也就是说,向量u的第i个分量与向量v的i个分量相乘,将结果保存在新向量的第i个分量中。在本书中,这个操作符只用于颜色向量的操作中。第5个操作符是在《Graphics Gems Ⅳ》书中引入的,它是作用在二维向量上的一元操作符,如果将这个操作符作用于向量v=(vx vy)T,那么就可以生成一个与v垂直的向量v⊥=(-vy vx)T。可以使用|a|来表示标量a的绝对值,|A|表示矩阵A的行列式。有时候,也使用|A|=|abc|=det(a,b,c),其中a、b、c是矩阵A的列向量。表1.2中的第9个操作符,也就是阶乘,可以用如下形式来定义(注意0!=1):
n!=n(n-1)(n-2)……3•2•1 (1.4)
第10个操作符,也就是二项式因子,可以用式(1.5)的形式来定义:
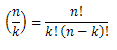 (1.5)
(1.5)
| 操作符 | 说明 |
|---|---|
| • | 点乘 |
| × | 叉乘 |
| vT | 向量v的转置 |
| ⊗ | 分段向量相乘 |
| ⊥ | 一元垂直点乘操作符 |
| |•| | 矩阵的行列式 |
| |•| | 标量的绝对值 |
| ||•|| | 变量长度(或者范数) |
| n! | 阶乘 |
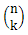 |
二项式因子 |
此外,可以称平面x=0、y=0、z=0为坐标平面(Coordinate Planes)或者轴对齐平面(Axis-aligned Planes),这组轴通常也称为标准基(Standard Basis)。如果没有特别注明,一般使用标准正交基(包括两个相互垂直的单位向量,具体参见附录A.3.1节)。
符号[a,b]表示所有位于a和b之间的数,其中包含a和b。如果希望所有的数处于a和b之间,但不包含a和b那么就可以写成(a,b)。此外,也可以将这两种表示结合起来使用,例如,[a,b)表示位于a和b之间,包含a但没有包含b。
在本书中也经常用到C语言中的数学函数atan2(y,x),它是数学函数arctan(x)的一种扩展。两者之间的主要差别是,-π/2<arctan(x)<π/2,0≤atan2(y,x)≤2π,而且在后面的函数中增加了一个额外变量,用来避免零除问题,也就是说x=y/x,但不能出现x=0。
| 函数 | 说明 | |
|---|---|---|
| 1 | atan2(y,x) | 两个量的反正切函数 |
| 2 |
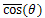 |
截取余弦函数 |
| 3 | log(n) | n的自然对数 |
截取余弦函数,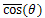 用于让着色方程便于阅读,如果余弦函数的结果小于零,那么通过这个函数返回的结果就是0。
用于让着色方程便于阅读,如果余弦函数的结果小于零,那么通过这个函数返回的结果就是0。
本书中的符号log(n)总是表示自然对数,即以e为底的对数loge(n),而不是表示以10为底的对数log10(n)。
在计算机图形学领域,对于三维几何体来说,右手坐标系是标准坐标系,所以在本书中也使用右手坐标系统(参见附录A.2节)。
最后,颜色可以用三元向量来表示,如(red,green,blue),其中每个元素的范围在[0,1]之间。
1.2.2 几何定义
大多数图形硬件使用的基本绘制图元是点、线、三角形(目前,我们知道的例外情况有像素平面(Pixel-Planes),它可以绘制球体;此外,还有NVIDIA NV1芯片,它可以进行椭圆体的绘制)。
在本书中几何实体集合一般指的是一个模型或者物体。一个场景是由很多模型组成的,这些模型位于需要绘制的环境中。场景还可以包括材质描述、光照,以及视场说明。
物体示例有小车、建筑物,甚至也可以是直线。在实际应用中,一个物体通常包含一组绘制图元,但也不是永远如此;物体可以具有一种比较高的几何表示形式,比如Bezier曲线或者表面、细分表面等。此外,物体还可以包含其他物体,比如,可以认为小车的门就是一个物体或者是小车的子集。
进一步阅读资料
与相关资源推荐你参考的最重要资源就是本书的网站:http://www.realtimerendering.com/,其中包含有最新信息,以及与每一章有关的相关网站链接。计算机实时绘制技术正在以“实时”的速度向前发展,所以在本书中,我们试图将重点集中在基本的概念,以及不可能过时的技术上。通过这个网站,我们给出了一些与今软件开发商相关的信息,从而可以使读者很好地跟踪当前的发展。
文件下载(已下载 2151 次)发布时间:2012/4/1 下午3:44:38 阅读次数:10148
