第八章 热力学定律参考资料

1．热力学定律

热力学第零定律 关于热平衡的一个定律。两个热力学系统如果分别与第三个系统处于热平衡，则它们彼此也处于热平衡，由此可推断，互为热平衡的所有系统具有一个取同样数值的状态参数，此参数被定义为“温度”。逻辑上该定律应优先于热力学第一定律和热力学第二定律，且事实上也已作为假设而包含在这两个定律之中，故名。

热力学第一定律 热力学的基本定律之一，是能量守恒定律在热力学问题中的表现形式，可表述为：外界传递给一个物质系统的热量与外界对系统所做的功之和等于系统内能的增量，也可表述为：第一类永动机是不可能制造的。

热力学第二定律 热力学的基本定律之一，是关于实际宏观过程进行的方向和条件的定律，有不同的表达方式：（1）不可能使热量自发地从低温物体传到高温物体而不引起其他变化；（2）任何热力循环发动机不可能将所接受的热量全部转变为机械功（即不可能制造第二类永动机）；（3）孤立系统内实际发生的过程总是使系统的熵增大（这一表述方式亦称“孤立系统熵增原理”）。

热力学第三定律 热力学的基本定律之一，是关于绝对零度不可能达到的定律，又称“能斯特热定理”。

1906年德国物理化学家能斯特根据凝聚态物质在低温下化学反应的性质所得出的热定理。可表述为：当温度趋于绝对零度时，系统的熵是一个常数，普朗克于1911年进一步假定这一常数为零，因此上述结论又可表述为：绝对零度时，任何凝聚态物质的熵等于零。上述结论还可等价地表述为：不可能利用有限步骤使物质系统的温度达到绝对零度；或绝对零度不可能达到。习惯上将最后一种说法称为“热力学第三定律”。

2．热力学温标

热力学温标也称为绝对温标或开尔文温标，这是建立在热力学第二定律基础上的最科学的温标，是由开尔文首先引入的。

根据卡诺循环的性质，在两个一定温度θ₁和θ₂之间工作的可逆热机与两个热源交换的热量Q₁，Q₂的比值为

Q₁/Q₂ ＝f（θ₁）/f（θ₂）

这里的f（θ）是一个普适函数，它的形式与温标θ的选择有关，如果我们选择温标T＝f（θ）就有

Q₁/Q₂ ＝T₁/T₂

这样定义的温标，就是热力学温标，根据上述定义，两个热力学温度的比值等于在这两个温度之间工作的可逆热机与热源交换的热量的比值，用热力学温标定出的温度数值，与测温物质的性质无关，因而是最科学的温标。

上述关系只是确定了热力学温度的比值，为了使热力学温度具有确定的数值，还必须选择固定点并确定分度方法。1954年国际计量大会规定水的三相点（固、液、气三相平衡共存的唯一状态）的温度为273.16K。这样定出的热力学温度的单位K（开尔文），就是水的三相点的热力学温度的1/273.16 。这样确定的热力学温标和教材中根据理想气体的性质确定的绝对温度是完全一致的。

因为在1个标准大气压下水的凝固点为273.15K（注意与水的三相点不同），而摄氏温标以这个温度为0℃，所以热力学温标与摄氏温标间有如下的关系：

t＝T－273.15K。

可见，水的三相点温度并非零摄氏度，而是0.01摄氏度。

制冷机 获得并维持低温的装置。其中的工作物质称为“致冷剂”，都是低沸点物质，如氨、二氧化碳、氟氯烷（俗称“氟利昂”）等。它们在室温、常压下是气体；在室温、高压（十倍大气压）下是液体。工作时，呈液态的工作物质经减压阀减压后汽化，自冷藏库（或室内）吸热，然后进入压缩机被绝热压缩，以至使它的温度升高到高于外界环境（或冷凝器中的冷却水）温度，从而向外界放热而液化。如此不断循环，就能将热量从低温处不断地抽取到温度较高的外界，并在此过程中消耗一定的机械功。制冷机的种类很多，有压缩式、吸收式、蒸气喷射式，此外还有利用珀耳帖效应的半导体制冷机等。

热泵 从温度较低的热源（如大气或河水）吸取热量，再向温度较高处（如室内）排放的装置。其工作原理与致冷机相同，热泵和致冷机的区别仅仅在于目的不同，前者将外界（大气或河水）当作低温热源，从那里吸热；后者将外界当作高温热源，向那里放热。例如，目前家庭中普遍使用的空调机，在冬季作为取暖设备使用时，就可称它为“热泵”；在夏季作为致冷设备使用时，就可称它为“制冷机”。

制冷机或热泵工作过程中有热量从低温区传到高温区，熵要减小。这似乎违反了热力学第二定律。但是，考虑到与此相伴随的（电）功转化为热的过程中，熵要增加。如果这种熵的增加量大于热量从低温区传到高温区过程中熵的减小量，从而使总系统的熵增加，那么这种过程并不违反热力学第二定律。

4．熵的定义

“熵”常用S表示，它定义为：一个系统的熵的变化Δs是系统吸收（或放出）的热量与绝对温度T之比，即

ΔS＝ΔQ/T ，

当系统吸收热量时，ΔQ取为正；当系统放出热量时，ΔQ取为负。这里我们定义的是熵的变化，而不是熵本身的值。让我们来考察热传导过程中熵的变化情况，设高温物体的温度为T₁，低温物体的温度为T₂。当一定的热量ΔQ从高温物体转移到低温物体的过程中，高温物体的熵变为ΔS₁＝－ΔQ/T₁ ，低温物体的熵变为ΔS₂＝＋ΔQ/T₂ ，总系统的熵变为ΔS＝ΔQ/T₂ －ΔQ/T₁ ，因为T₁＞T₂，所以ΔS＞0。这表明在热传导过程中“系统”的熵增加了！反之，如果热量从低温物体转移到高温物体，则因为ΔS₂＝－ΔQ/T₂ ，ΔS₁＝－ΔQ/T₁ ，所以系统的熵变ΔS＜0，即系统的熵减小了！

自然界实际过程的方向性表明，总熵增加的过程才是能够自发发生的过程，热量从高温物体传向低温物体时，总系统的熵增加，所以这样的过程能自发发生；热量从低温物体传向高温物体时，总系统的熵减少，所以这样的过程不能自发发生。

5．实际过程不可逆性的解释——统计规律性

熵增加原理可以从大量分子运动的统计规律性得到解释。

如图8－3所示，A、B是一个盛有气体的容器中体积相等的两个区域。从统计物理学的观点来看，对于任何一个气体分子来说，它的运动是无序的，它随时可能从A区域运动到B区域，或从B区域运动到A区域，所以它出现在A区域或B区域的机会相等，均为1/2 。两个分子在容器中的分布有4种可能性（请列出这4种不同的可能分布）。因此它们同时出现在A（或B）区域的概率是1/4 ，即（1/2 ）²。三个分子在容器中的分布有8种可能性（请列出这8种不同的可能分布）。因此它们同时出现在A（或B）区域的概率是1/8 ，即（1/2 ）³。以此类推，如果容器中有n个分子，那么它们自发地同时出现在A（或B）区域的概率是（1/2 ）ⁿ。

图8-3

通常，一摩尔气体的分子数是N_A＝6.022×10²³。所以，这些气体分子自发地同时出现在A（或B）区域概率的量级是（1/2 ）¹⁰²³。可见，气体分子集中在容器中某一区域的概率非常小，实际上可认为是不可能发生的。而气体分子在客器中均匀分布的概率却非常大。这就是为什么气体分子总是趋向均匀分布的原因。

类似地，当两个温度不同的物体相互接触时，热量从高温物体传向低温物体的概率非常大，其相应逆过程的概率则非常小，所以实际上热量从低温物体传向高温物体的现象是不可能发生的。

总之，在一个孤立系统内，一切实际过程总是向概率大的状态变化的，所以总具有一定的方向性。

根据统计物理学的观点，熵是系统无序程度的量度，在图8－3所示的例子中，气体分子集中在容器中的某个区域是一种最有序的情况，此时系统的熵最小；气体分子在容器中均匀分布是一种最无序情况，此时系统的熵最大。可见，熵大，即出现的概率大，意味着“混乱”和“分散”；熵小，即出现的概率小，意味着“整齐”和“集中”。气体分子趋向均匀分布的过程是向概率大的状态变化的过程，也正是熵增加的过程，于是，利用统计规律性对熵增加原理作出了解释。

6．麦克斯韦妖与信息

麦克斯韦也给热力学第二定律出过一个难题，他设想有一个能观察到所有分子的轨迹和速度的小精灵把守着气体容器内隔板上一小孔的闸门，见到这边来了高速运动的分子就打开闸门让它到那边去，见到那边来了低速运动的分子就打开闸门让它到这边来。设想闸门是完全没有摩擦的，于是这小精灵无需作功就可以使隔板两侧的气体这边愈来愈冷，那边愈来愈热。这样一来，系统的熵降低了，热力学第二定律受到了挑战。人们把这个小精灵称为麦克斯韦妖（Maxwell demon）。

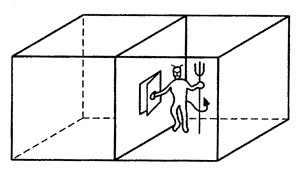
图8-4麦克斯韦妖

麦克斯韦妖可不是人们想象中的那种呼风唤雨魔法无边的巨灵，它与普通人相比，除了具有非凡的微观分辨力之外，别无他长。也就是说，麦克斯韦妖小巧玲珑，是纯智能型的，可是只凭这一点，它就能干出惊人之举，尽管许多人想弄清这小妖精的来头，直到1929年它的底细才开始被匈牙利物理学家西拉德（L.Szilard）所戳穿。

麦克斯韦妖有获得和储存分子运动信息的能力，它靠信息来干预系统，使它逆着自然界的自发方向行进。按现代的观点，信息就是负熵，麦克斯韦妖将负熵输入给系统，降低了它的熵。那么，麦克斯韦妖怎样才能获得所需的信息呢？它必须有一个温度与环境不同的微型光源去照亮分子，这就需要耗费一定的能量，产生额外的熵。麦克斯韦妖正是以此为代价才获得了所需信息（即负熵）的，这额外的熵产生补偿了系统里熵的减少。总起来说，即使真有麦克斯韦妖存在，它的工作方式也不违反热力学第二定律。

【摘自赵凯华，罗蔚茵，《新概念物理教程：热学》高等教育出版社，P。208（1998，2002）】

7．“说热机效率 话冷却塔”

1712年，英国人托马斯•纽可曼（Thomas Newcomen，1663～1729）发明了大气压蒸汽机，这种机器具有汽缸与活塞，在工作时，先把蒸汽导入汽缸，这时汽缸停止供汽而汽缸内进水，蒸汽便遇冷凝结为水使汽缸内气压迅速降低，就可以使水吸上来。之后再把蒸汽导人汽缸，进行下一个循环，最初的这种蒸汽机大约每分钟往返10次，而且可以自动工作，使矿井的抽水工作大为便利，所以不仅英国人使用，在德国与法国也在使用，这种机器被称为“矿山之友”。

蒸汽机不是英国人瓦特（James Watt，1736～1819）的发明，瓦特的贡献是对蒸汽机进行了一系列改进，其中最重要的改进有两项，一项是发明了冷凝器，大大提高了蒸汽机的效率，另一项是发明了离心调速器，使蒸汽机速度可自由控制。之后的蒸汽机才真正在工业上被普遍使用。

最早从理论上讨论蒸汽机的热效率的是法国人卡诺（Nicolas Léonard Sadi Carnot，1796-1832）。卡诺的结论是，热机的最高效率取决于热机内的温度差。对于一般的蒸汽机来说，令T₁是蒸汽的绝对温度，T₂是冷凝器的绝对温度，则热机所能达到的最大效率为η＝（T₁－T₂）/T₁。

卡诺研究的结论启示我们，要提高热机的效率必须向两个方向去努力：其一是提高机器入口处介质的温度T1，其二是降低机器出口处介质的温度T2。提高温度T1有一个限制，这就是热机材料在高温下会变得不结实。例如钢铁，在1200℃就会熔化，不能承受任何压力，在600℃以上就会变软，在一定的高压下会缓慢地变形而导致破坏。所以通常用钢铁制造的蒸汽机或汽轮机，蒸汽的温度大约不能超过560℃，即绝对温度大约不超过833K。一般航空用的发动机，是用特殊材料制造的，燃气温度可以达到1200℃。由于入口温度提高，效率会提高许多，因此为了提高蒸汽机入口的温度，需要研究新的耐高温的材料。

普通可行的提高热机效率的办法，是降低热机出口的温度。这就是，要对热机出口的介质进行冷却。就以通常的汽轮发电机来说，它的蒸汽入口温度是大约560℃（833K）。出口温度大约是40℃（313K），它的热效率是0.62。这个效率当然是在十分理想的情况下计算得到的。实际用燃烧煤来发电，效率还会因为锅炉和其他部分的热损失而降低很多，现在如果把出口温度降低10℃，效率就会变成0.64。即效率提高了0.02。如果把它换算成输出功的百分比，降温得到的输出功率就增加了3%。

可别小看这通过降低出口温度而提高的这3%的输出功率。就以华北电网来说，它的发电装机容量大约是7000万千瓦，它的3%是210万千瓦，按通常的城市电费以每度（每千瓦时）0.4元人民币来计算。210万千瓦，每小时电费是84万元，每天就是2016万元。一年就可以达到70多亿元人民币！这是一个相当大的数字。所以靠降低热机出口温度来提高效率，节约能源的效果是相当可观的。

用什么办法来使汽轮机的出口温度降低呢？自然界最容易得到的，热容量又比较大的物质就算水了。所以通常都是用水来冷却的。一座大型发电厂对冷却水的需求量之大是惊人的。一台十万千瓦的发电机，大约需要3m²/s的水流量去冷却，就是说一座百万千瓦的发电厂，需冷却水约30m³/s。需知北京市的用电量是数百万千瓦，而北京城边的永定河平均流量只有20m³/s左右，何况天旱时河水还会断流。而且直接用河水冷却后，水温上升，再排入河中，还会产生热污染的严重问题。冷却塔就是为了解决这一难题而建造的。

冷却塔的工作原理如图8－5，冷却热机的水被热机加热后，用泵打到塔筒的淋水装置的高端，然后以淋水方式喷洒下来，在降落的过程中，水被空气冷却了而空气却被加热了，加热后的空气比重减小，所受浮力增大，在浮力作用下，空气上升到塔顶冒出。塔愈高，空气浮力愈大，空气上升速度也愈大，冷却效率也愈好（图8－6）。

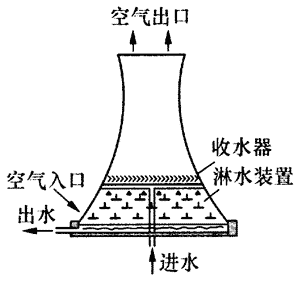
图8-5 冷却塔示意图

图8-6

冷却后的水降入水池，然后再被用于冷却热机，循环不已，所以冷却塔在缺水区建电厂是绝对必需的，用冷却塔冷却可以比用直流水冷却省水97%，并且使水温平均降低11℃，其中3%的水是随空气上升的水蒸气散发到空气中去了。

对于缺水的地区，损失的这3%的水，其数量也是相当可观的。为了节约这部分水，冷却塔被做成“干式”的。即热交换不是用水淋下来的方式，而是让热水通过像暖气片那样的热交换器来实现，水蒸气就不会跑到大气中去了。不过，干式冷却塔的效率一般来说要低些。

上面说的是发电热机的冷却问题，对于制冷机、空调机等设备，为了提高效率，也有冷却的问题。特别是对于那种大型建筑的集中空调或大型冷库，也需要在房顶或适当的地方建造一个冷却塔，不过这种冷却塔规模很小，没法和发电厂的冷却塔相比，如图8－7就是一座典型的这类冷却塔。

图8－7小型冷却塔

为了提高航空发动机的效率，也需要冷却发动机出口的温度，不过这时就不能使用水来冷却了，一般要使用快速流动的空气或别的介质，这类高效率的冷却方案需要更精细的研究。而提高冷却的效率，不管对蒸汽机、汽轮机、燃气轮机，还是对制冷机，迄今一直是人们努力研究的方向。

【摘自《物理教学》Vol.29，No.3（2007.3）；作者：武际可】

发布时间：2012/3/1 下午3:07:48  阅读次数：3475