重力在大气压强产生中的作用
孙成永 江苏盐城中学 选自《物理教师》2011年第1期
关于大气压强可以有两种解释:第一;由于地球对空气的吸引作用,空气压在地面上,就要靠地面或地面上的其他物体来支持它,这些支持着大气的物体和地面,就要受到大气压力的作用,单位面积上受到的大气压力,就是大气压强;第二;可以用分子动理论的观点解释。因为气体是由大量的做无规则运动的分子组成,而这些分子必然要对浸在空气中的物体不断地发生碰撞。每次碰撞,空气分子都要给予物体表面一个冲击力,大量空气分子持续碰撞的结果就体现为大气对物体表面的压力,从而形成大气压。单位体积中含有的分子数越多,则相同时间内空气分子对物体表面单位面积上碰撞的次数越多,因而产生的压强也就越大。
正因为有以上两种解释使得很多人产生了疑惑:用分子运动的观点解释,则大气压强只与气体分子的密度、运动速度等有关,从宏观的物理量上看只与气体的温度和体积有关,而我们周围的大气可以看成理想气体,气体分子之间相互作用忽略不计、气体分子之间不受重力影响,这说明大气压强与气体自身的重力无关。由于大气压强可以有两种解释产生了这样一个问题:用瓶子封闭一个大气压的空气,如果把这个瓶子放到宇宙飞船中,则这时瓶子里的气体的压强为多少?若把这瓶密闭的空气放到月球上,里面的大气压又是多少?两种解释会得到不同的结论:用大气压强是由于大气层受到重力作用而产生的,得到的结论是瓶子里大气压强为零;用分子动理论的观点解释,则瓶子的气体压强不变,还是一个大气压,到底哪一种结论正确呢?我们必须对大气压强有一个全面且正确的认识,才能回答上述问题。
为了彻底的弄清大气压强的有关问题,本文从以下4个方面来分析:
1.经典物理对大气压强的认识
经典物理关于气体有两个基本假设,一是分子运动论,二是理想气体模型。经典物理认为气体对某一个面的压强是由大量的气体分子对这个面的碰撞而产生的,其压强大小等于单位时间内大量气体分子对单位面积的器壁的冲量,从理想气体微观模型出发可以推出理想气体的压强公式为
p=nkT (1)
从(1)式可看出理想气体压强与气体的数密度n成正比,与热力学温度T成正比,其中是为玻尔兹曼常量,数值为:k=1.3806505×10-23J/K,分子数密度越大,温度越高,压强越大。
2.大气压强与空气重量关系的定量分析
根据分子运动论,玻尔兹曼把麦克斯韦速度分布律应用在重力场中得到玻尔兹曼分布律,公式为
n=n0
 (2)
(2)
其中m为气体分子的质量,Z为铅直方向的坐标,若地面为坐标原点,那么表示距地面的竖直高度,n0为z=0处的气体的数密度,根据(2)式可计算出在某一给定的温度下,在高度为z处的空气分子数密度n。
在一定温度T下,由(1)、(2)式可得到气体压强随高度变化的关系p=n0kT
 。当z=0时p0=n0kT,即表示在z处的大气压强p=p0,所以
。当z=0时p0=n0kT,即表示在z处的大气压强p=p0,所以
p=p0 (3)
(3)
从(3)式可见,若温度T不变,压强仅为高度的函数。若在大气层中,取一竖直方向的坐标,设气柱内各点温度相同,对(3)式微分可得
dp=-ρgdz。 (4)
ρ表示气体的密度,式中负号表示压强随高度的增加而减小,因为若在竖直高度上有一微小高度的增量(dz>0),必然使压强减小|dp|(dp<0),从(4)式还可以看出,在高度z~z+dz之间,大气压强减小量与高度z处密度ρ成正比。所以在地面附近比高空的大气压强随高度变化要显著。
设大气层高为h(理论上也可视为h→∞),坐标为z[0,∞]区间,当z→∞时,气体压强为零。坐标区间所对应的压强区间为[p0,0],对(4)式两边积分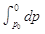 =
=
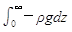 ,得0-p0=-g
,得0-p0=-g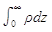 ,所以p0=g
,所以p0=g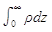 ,两边乘以气柱截面积S得
,两边乘以气柱截面积S得
p0S=g
 =g
=g
 =g
=g
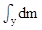 =Mg=G
=Mg=G
则p0=G/S ,p0为在z=0处大气压强的值。G表示由z=0处到大气顶层的气柱的重量。
上式明确地阐明了大气压与空气重量的关系,式子的物理意义是大气压在数值上等于单位截面积的整个空气柱的重量,因此在不要求本质地研究大气压产生的原因时,可以说大气压是由空气重量引起的。
如果把一个开口容器用盖封闭起来,容器里封闭一部分气体,严格地说容器内气体的压强是由气体分子碰撞的结果。因为此时这部分气体与开口时相比较,其气体的密度和温度都没有改变,那么容器内气体的压强仍为一个大气压 。
3.大气压随高度变化
我们知道离地面越高,空气越稀薄,空气的密度越小,因此大气压随高度减小是不均匀的,越高大气压随高度减小得越慢。“在海拔2km以内,可以近似地认为每升高12m,大气压降低1毫米汞柱。”
为了较深刻理解这段教材,我们仍用分子运动论的理论作一些必要的分析和研究。由上面得出的等温压强公式p=p0 很容易分析大气压随高度变化的两个规律:(1)大气压随高度的增加而减少,当z→∞,则p→0;(2)大气压随高度的增加而减少是不均匀的,越高大气压随高度减小得越慢,下面再作定量的研究。根据公式n=n0
很容易分析大气压随高度变化的两个规律:(1)大气压随高度的增加而减少,当z→∞,则p→0;(2)大气压随高度的增加而减少是不均匀的,越高大气压随高度减小得越慢,下面再作定量的研究。根据公式n=n0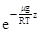 (式中R为理想气体常数,等于玻尔兹曼常数乘以阿伏伽德罗常数,μ为摩尔质量。)可知
(式中R为理想气体常数,等于玻尔兹曼常数乘以阿伏伽德罗常数,μ为摩尔质量。)可知
ρ=nm=n0m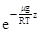 =ρ0
=ρ0
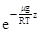 (5)
(5)
其中ρ0=n0m,即ρ0为z=0(设海平面)处气体的密度。在标准状况下(温度为0℃,一个标准大气压强)ρ0=1.29k/m3,又dp=-ρgdz,所以
dz=-dp/ρg (6)
由(5)式代入(6)式可得 dz=- (7)
(7)
(7)式表明了大气压随高度不同其变化率是不均匀的,这样在一定的温度下(例如T=273K)给定某一确定的高度应用(7)式可求出dz。为了便于比较,注意式中的dp应取1mmHg,即dp=1mmHg柱高=1.333×102Pa。例如z=100m,T=273K,由(7)式可计算得dz=10.7m。此结果告诉我们在海拔100m附近每升高10.7m大气压降低1mm汞高,依照上面方法可得出2km内不同的高度对应的dz值,根据计算结果列表1。
| 海拔高度z/m | 0 | 100 | 200 | 400 | 800 | 1000 | 1600 | 2000 |
| 空气密度/kg•m3 | 1.29 | 1.27 | 1.26 | 1.23 | 1.17 | 1.15 | 1.07 | 1.01 |
| dz /m | 10.5 | 10.7 | 10.8 | 11.1 | 11.6 | 11.8 | 12.9 | 13.5 |
从表1中可以看出在海拔1km以内,每升高11m左右大气压下降1mmHg,在1km至2km,每升高12m左右,大气压下降1mmHg,在初中物理中讲“海拔2km以内,可以近似地认为每升高12m大气压降低1mm汞柱,”这里结论是平均值。
4.计算大气层气体的总重量
解法1。根据对大气压的认识,大气压强等于地面单位面积上所受到的空气对它的压力,它的大小应等于单位截面空气柱的重力,所以整个大气层所产生的重力为:G=p04πR2,4πR2为地球整个表面积,代入有关数据可得,G1=5.214×1019N,这种解法有近似性,因为p0的意义是表示单位截面的从z=0开始无限高柱体内气体的重量。我们可以想象式子G1=p04πR2是大量的柱体组合而成,因为各柱体上、下截面是相等的,当离开地面一段距离后各个柱体是离开的,在应用上式时各柱体狭缝间一部分空气没有计算进去,为了使大气层所有气体分子都被计算进去,根据分子运动论的理论计算,可以得到满意的解答。
解法2。应用公式n=n0 用积分法求解,围绕地球的大气层的气体分子总数为
N总=
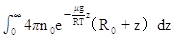 ,
,
R0为地球半径,积分得
N总=4πn0[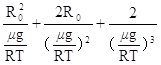 ]。
]。
所以大气层气体总重量为
G2=N总mg=4πn0mg[
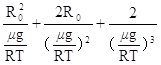 ]
]
代入数据可得:G=5.230×1019N
从这两种结果不难看出,解法2比较准确,解法1比较近似,但两种解法所得出的大气层气体的总重量相差不很多,说明在不要求从本质上研究大气压强采用重力是产生大气压的认识仍是可行的,对解决某些问题带来很大方便。
由(2)式我们可以得出结论:大气压强和气体压强一样,都是由于大量气体分子对器壁不断碰撞的结果。正因为这样,大气压的大小与大气所受重力的大小无关,只决定于所在处气体的密度和温度,但从(1)式和(3)式我们也清楚地看到:地球重力的作用使空气密度和大气压随高度的增加而发生变化,在地球引力为零的地方,即z=∞时,n=0,p=0。
综上所述,在瓶子里封闭一个大气压的空气若保持体积和温度不变的情况下,里面气体压强总是一个大气压,而与气体所受重力情况无关。
文件下载(已下载 3097 次)发布时间:2012/1/6 下午3:12:02 阅读次数:16670
