10.粗糙均匀小球间的碰撞
前一篇文章中我们讨论了光滑均匀小球间的碰撞,这种情况下其实小球是作为质点处理的。若小球是粗糙的,就不能忽略小球的大小,需要考虑接触面间的摩擦力,进一步求出摩擦力产生的冲量,这个冲量即会影响小球的线速度,还会使小球产生转动效果。
碰撞检测代码没有什么变化,而在碰撞反应代码中需要处理碰撞切线方向的冲量。还是以上一篇文章类似的两球碰撞情况为例说明具体原理。
如下图所示,质量为2kg,半径为2m的小球m1以初速度v10=5m/s向上运动,同时以角速度ω10=-1rad/s旋转(“-”表示逆时针方向转动);而质量为3kg,半径为3m的小球m2静止不动。
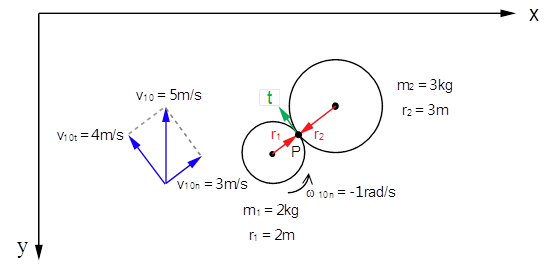
图1 两个粗糙小球间的碰撞
首先我们需要找到接触点P在世界空间中的坐标,对于两个球体来说是非常简单的。假设此时两球质心的坐标分别为C1=6i+13j,C2=10i+10j,则:
P.X=C1.X+(C2.X-C1.X)r1/(r1+r2)=6+4×2/5=7.6
P.Y=C1.Y+(C2.Y-C1.Y)r1/(r1+r2)=13-3×2/5=11.8
然后获取小球质心指向接触点的矢量:
r1=P-C1=1.6i-1.2j
r2=P-C2=-2.4i+1.8j
因为我们现在将小球看成刚体,因此关心的接触点P的速度而不是质心的速度,这也是与上一篇文章最主要的不同点之一。
已知质心速度,要求刚体上任一点的速度,需要用到以下公式计算:
vP=vC+ω×r
前面的文章已经讨论过,在物理上ω是一个矢量,在2D的情况中,ω的方向只有两种可能,垂直于平面向上或向下。如上图所示,根据右手螺旋定则,四指由+x轴转向+y轴,旋转方向为顺时针,此时大拇指指向纸内,即+z方向为垂直纸面向里。因此,在2D的情况下,只用一个标量就可以表示ω,当它为正时表示顺时针旋转,为负时表示逆时针旋转。
但叉乘只有在3D向量中才有几何意义,若u=(u1,u2,u3),v=(v1,v2,v3),则n×v=(u2v3-u3v2,u3v1-u1v3,u1v2-u2v1)。而标量ω实质上是ω=(0,0,ω),二维矢量r实质上是三维矢量r=(rx,ry,0),根据叉乘的定义,标量ω与二维矢量r的叉乘可以这样计算:
ω×r=(-ωry,ωrx,0)
这个算法其实已经写在了引擎的MathUtils类的Cross的一个重载方法中了,代码如下:
////// 拟叉乘,一个标量与二维矢量叉乘的结果是一个二维矢量 /// /// 标量</param> /// 二维矢量</param> ///二维矢量 public static Vector2 Cross(float s, Vector2 a) { return new Vector2(-s * a.Y, s * a.X); }
所以m1上接触点P的速度为:
v10=(0i-5j)+((1×-1.2)i+(-1×1.6)j)=-1.2i-6.6j
因为m2保持静止且不旋转,所以:
v20=0
接触点的相对速度为:
vr=v10-v20=-1.2i-6.6j
法线矢量n为球1质心指向球2质心的单位矢量,即n=0.8i-0.6j,进一步就可以求出相对法线速度:
vrn=vr•n=-1.2×0.8+(-6.6)×-0.6=3m/s(这个结果与光滑小球相撞的情况是相同的)
有了相对法线速度,我们就可以计算法线方向的冲量In(设e=1):
In=-vrn(1+e)/(1/m1+1/m2)=-3×2/(0.5+1/3)=-7.2N•s
然后将In分解到x,y方向分别计算x,y方向的速度变化量:
Inx=In•n.X=-5.76 N•s
v1x=v10x+Inx/m1=0+-5.76/2=-2.88m/s
Iny=In•n.Y=4.32 N•s
v1y=v10y+Iny/m1=-5+4.32/2=-2.84m/s
以上步骤和上一篇文章是相同的,唯一的变化就是相对速度指的是接触点的相对速度而不是质心的相对速度。
切线方向的处理
与处理法线方向的情况类似,我们需要求出相对切线速度,首先需要知道切线矢量t,因为切线必垂直于法线,所以将法线逆时针旋转90度就可以获取切线矢量。已知n=0.8i-0.6j,则:
t.X=n.Y=-0.6
t.Y=-n.X=-0.8
即:
t=-0.6i-0.8j
这样就可以求出相对切线速度:
vrt=vr•t=-1.2×-0.6+-6.6×-0.8=6m/s
然后怎样求切线方向的冲量呢?这涉及到物理中滑动摩擦力的知识。滑动摩擦力产生的条件是接触面间要有相对滑动,因此当vrt不等于零时,我们需要进一步计算它产生的效果。根据物理知识,接触面间的滑动摩擦力正比于接触面间的正压力,公式为:
f=μN
其中比例系数μ称为动摩擦因数,它的大小是由两物体的材料性质、粗糙程度等决定的,下表是常见的几种材料间的动摩擦因数
| 材料 | 钢—钢 | 木—木 | 木—金属 | 钢—冰 | 木头—冰 |
| 动摩擦因数 | 0.25 | 0.30 | 0.20 | 0.02 | 0.03 |
而正压力正比于法线方向的冲量,因此有:
It=μIn
式中It和In分别为切线和法线方向的冲量。
若取μ=0.2,则法线方向的冲量为
It=μIn=0.2×-7.2=-1.44N•s。
Itx=It•t.X=0.864 N•s
v1xʹ=v1x+Itx/m1=-2.88+0.864/2=-2.448m/s
Ity=It•t.Y=1.152 N•s
v1y=v10y+Iny/m1=-2.84+1.152/2=-2.264m/s
而且切线方向的冲量还会是物体产生转动效果影响它的角速度:
ω1t=ω10+r1×It/I
式中It为切线方向冲量(矢量),I为物体的转动惯量(标量),m1的转动惯量I为m1r12/2=4。以上公式化成标量式即:
ω1t=ω10+(r1xIty-r1yItx)/I=-1+(1.6×1.152+1.2×0.864)/4=-0.28rad/s。
即碰撞后小球1的旋转速度变小。
正确的切线方向
但这个代码还隐藏着一个错误,我们来讨论一下这种情况:如下图所示,质量为2kg,半径为2m的小球m1以初速度v10=5m/s向上运动,同时以角速度ω10=1rad/s顺时针旋转;而质量为3kg,半径为3m的小球m2静止不动。其实就是上一种情况的镜像。
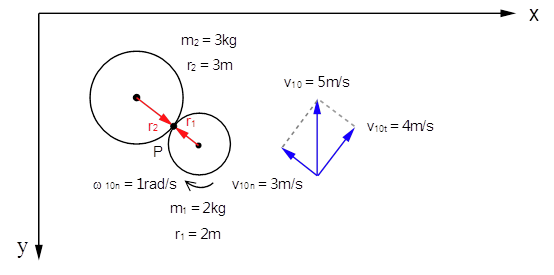
图2 正确的切线方向
这种情况中,各个相关矢量为:
n=-0.8i-0.6j
r1=-1.6i-1.2j
vr=v10=1.2i-6.6j
vrn=3m/s
vrt=-6m/s
In=-7.2N•s
It=-1.44 N•s
t=-0.6i+0.8j
Itx=It•t.X=0.864N•s
最后一个公式的计算结果是错误的,从图中明显可以看出,碰撞后切线冲量在x方向上的分量为负,而根据公式计算出的结果为正,Ity的算式没有列出,但结果也是与实际情况正好相反。
问题出在哪里?是切线算法有误!我们是通过将法线逆时针旋转90度获取切线的,但是将法线顺时针旋转90度也是切线,到底应该使用哪个切线?需要满足切线方向与相对切线速度方向一致,有个这个限制,切线矢量的计算式应为:
t=(n×vr)×n
根据叉乘恒等式,以上公式可以进行化简:
t=(n×vr)×n
=(n•n)vr-(vr•n)n
=vr-vrn n
=1.2i-6.6j+-3(-0.8i-0.6j)
=3.6i-4.8j
然后进行归一化,最后结果为:
t=0.6i-0.8j
与上面的错误切线恰好反向一直线,如果代入这个正确切线,计算结果就不会出错了!
但是在代码中仍然使用将法线逆时针旋转90度的错误计算公式,而没有使用这个正确的计算公式,理由是这个算法比较消耗资源。我们可以判断相对切线速度的大小,若它小于0,就将法线冲量取反,这样只需计算一次就可以获得同样的正确结果。
代码实现
弄清了物理原理,现在SolveCollision方法中的代码如下:
#region 碰撞检测临时变量
float r; // 两球半径之和
float distSqr; // 两球球心间距离平方
Vector2 normal; // 碰撞法线矢量
Vector2 tangent; // 碰撞切线矢量
float normalImpulse; // 法线方向的冲量
float normalMass; // 计算法线冲量时用到的等效质量
float tangentImpulse; // 切线方向的冲量
float vrn; // 接触点相对速度的法线分量
float vrt; // 接触点相对速度的切线分量
Vector2 vA; // BodyA的线速度
Vector2 vB; // BodyB的线速度
float wA; // BodyA的角速度
float wB; // BodyB的角速度
Vector2 contactPoint; // 碰撞接触点
#endregion
private void SolveCollision(Body bodyA, Body bodyB)
{
// 缓存两个Body的线速度和角速度
vA = bodyA.LinearVelocityInternal ;
vB = bodyB.LinearVelocityInternal;
wA = bodyA.AngularVelocityInternal ;
wB = bodyB.AngularVelocityInternal;
// 计算两个Body的半径之和
r = bodyA.Radius + bodyB.Radius;
// 计算两球心间距离的平方
distSqr = (bodyA.Position.X - bodyB.Position.X) * (bodyA.Position.X - bodyB.Position.X) + (bodyA.Position.Y - bodyB.Position.Y) * (bodyA.Position.Y - bodyB.Position.Y);
// 通过比较d平方和r平方判断是否发生碰撞。这里没有使用d.Length()和r比较,因为计算d的大小涉及开方操作比较耗费资源。
bool isTouching = distSqr <= r * r ? true : false;
// 计算球A质心指向球B质心的矢量,即法线矢量。normal=bodyB.Sweep.C - bodyA.Sweep.C的内联写法
normal.X = bodyB.Sweep.C.X - bodyA.Sweep.C.X;
normal.Y = bodyB.Sweep.C.Y - bodyA.Sweep.C.Y;
// 以下三行代码对法线normal进行归一化,即法线的单位向量。normal.Normalize()的内联写法。
float factor = 1f / (float)Math.Sqrt(normal.X*normal.X+normal.Y*normal.Y);
normal.X *= factor;
normal.Y *= factor;
// 碰撞切线矢量,相当于相对法线逆时针旋转90度
tangent = new Vector2(normal.Y, -normal.X);
// 获取接触点在世界空间中的坐标
float ratio = bodyA.Radius / r;
contactPoint.X = bodyA.Position.X + (bodyB.Position.X - bodyA.Position.X) * ratio;
contactPoint.Y = bodyA.Position.Y + (bodyB.Position.Y - bodyA.Position.Y) * ratio;
// 计算接触点与两球质心间的矢量
Vector2 rA = contactPoint - bodyA.Sweep.C;
Vector2 rB = contactPoint - bodyB.Sweep.C;
// 接触点法线方向的相对速度。
// 数学知识告诉我们:这个值为正表示相对法线速度方向与法线方向的夹角小于90度,即两球正在相互靠近
vrn = normal.X * ((vA.X - wA * rA.Y) - (vB.X - wB * rB.Y)) + normal.Y * ((vA.Y + wA * rA.X) - (vB.Y + wB * rB.X));
// 接触点切线方向的相对速度。
vrt = tangent.X * ((vA.X - wA * rA.Y) - (vB.X - wB * rB.Y)) + tangent.Y * ((vA.Y + wA * rA.X) - (vB.Y + wB * rB.X));
// 若d小于等于r且正在相互靠近则说明发生碰撞
if (isTouching && vrn > 0)
{
// ----------------------------
// 处理法线方向的碰撞
// ----------------------------
// 碰撞时法线方向受到的冲量的公式为:
// In=-vrn(1+e)/(1/m1+1/m2)
// 可将1/(1/m1+1/m2)看成一个等效质量normalMass
normalMass = 1.0f / (bodyA.InvMass + bodyB.InvMass);
// 恢复系数取为两个球体恢复系数的平均值
float restitution = (bodyA.Restitution + bodyB.Restitution) / 2;
// 根据公式计算法线方向的冲量
normalImpulse = -normalMass * vrn * (1 + restitution);
// 在两个刚体上施加法线方向的冲量
bodyA.LinearVelocityInternal.X += bodyA.InvMass * normalImpulse * normal.X;
bodyA.LinearVelocityInternal.Y += bodyA.InvMass * normalImpulse * normal.Y;
bodyB.LinearVelocityInternal.X -= bodyB.InvMass * normalImpulse * normal.X;
bodyB.LinearVelocityInternal.Y -= bodyB.InvMass * normalImpulse * normal.Y;
// ----------------------------
// 处理切线方向的碰撞
// ----------------------------
// 只有切线方向有相对运动时才会产生摩擦力效果
if (vrt != 0)
{
// 切线方向的冲量即动摩擦因数乘以法线方向的分量
tangentImpulse = normalImpulse * (bodyA.Friction + bodyB.Friction) / 2;
// 如果相对速度为负,则冲量取反
if(vrt<0)
tangentImpulse *= -1.0f;
// 获取x、y方向上的切线冲量的分量
float Ix = tangentImpulse * tangent.X;
float Iy = tangentImpulse * tangent.Y;
// 在两个刚体上施加切方向的冲量
bodyA.LinearVelocityInternal.X += bodyA.InvMass * Ix;
bodyA.LinearVelocityInternal.Y += bodyA.InvMass * Iy;
wA += bodyA.InvInertia * (rA.X * Iy - rA.Y * Ix);
bodyB.LinearVelocityInternal.X -= bodyB.InvMass * Ix;
bodyB.LinearVelocityInternal.Y -= bodyB.InvMass * Iy;
wB -= bodyB.InvInertia * (rB.X * Iy - rB.Y * Ix);
// 更新刚体的角速度
bodyA.AngularVelocityInternal = wA;
bodyB.AngularVelocityInternal = wB;
}
}
}
Silverlight示例
在silverlight中,MainPage.xaml.cs的代码如下:
namespace Stun2DPhysics4SLDemo
{
public partial class MainPage : UserControl
{
// 当一帧绘制结束时保存当前时刻
private DateTime LastTick;
// 物理引擎
World World;
// 保存Sprite的集合
private List<SpritePhysice> sprites;
SphereSprite ball0;
Line line;
// 小球的属性
float radius = 20.0f;
float density = 1.0f;
float linearDamping = 0.1f;
float angularDamping = 0.3f;
// 光标坐标
double mouseX;
double mouseY;
string sTxtFriction = "按数字键1切换动摩擦因数:";
string sTxtRestitution = "按数字键2切换弹性系数:";
bool isRunning = false;
double totalTime = 0;
int fps = 0;
public MainPage()
{
InitializeComponent();
World = new World(new Vector2(0, 150));
sprites = new List<SpritePhysice>();
ball0 = new SphereSprite(LayoutRoot, new Point(100, 290), World, radius, density, Colors.White, "0");
sprites.Add(ball0);
SphereSprite ball2 = new SphereSprite(LayoutRoot, new Point(100, 140), World, radius, density, Colors.Yellow, "2");
sprites.Add(ball2);
SphereSprite ball3 = new SphereSprite(LayoutRoot, new Point(100, 240), World, radius, density, Colors.Green, "3");
sprites.Add(ball3);
SphereSprite ball4 = new SphereSprite(LayoutRoot, new Point(100, 340), World, radius, density, Colors.Brown, "4");
sprites.Add(ball4);
SphereSprite ball5 = new SphereSprite(LayoutRoot, new Point(400, 240), World, radius, density, Colors.Blue, "5");
sprites.Add(ball5);
SphereSprite ball6 = new SphereSprite(LayoutRoot, new Point(475, 240), World, radius, density, Colors.Magenta, "6");
sprites.Add(ball6);
SphereSprite ball7 = new SphereSprite(LayoutRoot, new Point(725, 240), World, radius, density, Colors.Black, "7");
sprites.Add(ball7);
float firstRedBallX = 550f;
float firstRedBallY = 240f;
int n = 4;
for (int i = 0; i < n; i++)
{
float redBallX = firstRedBallX + 2 * radius * i * (float)Math.Cos (MathHelper .Pi /6);
int k = -i;
for (int j = 0; j < i+1; j++)
{
float redBallY = firstRedBallY + k * radius;
SphereSprite ball = new SphereSprite(LayoutRoot, new Point(redBallX, redBallY) , World, radius, density, Colors.Red, "1");
k=k + 2;
sprites.Add(ball);
}
}
// 设置小球的阻尼系数
foreach (SphereSprite s in sprites)
{
s.Body.LinearDamping = linearDamping;
s.Body.AngularDamping = angularDamping;
}
// 显示小球0和光标之间的连线
line = new Line();
line.Stroke = new SolidColorBrush(Color.FromArgb(255, 255, 255, 255));
line.StrokeThickness = 2;
LayoutRoot.Children.Add(line);
txtFriction.Text = sTxtFriction+"0.2";
txtRestitution.Text = sTxtRestitution+"1";
}
private void CompositionTarget_Rendering(object sender, EventArgs e)
{
// 保存自上一帧以来流逝的时间
TimeSpan elapsedTime = (DateTime.Now - LastTick);
// 计算帧频
totalTime += elapsedTime.TotalSeconds;
fps += 1;
World.Step ((float)elapsedTime.TotalSeconds );
for (int i = 0; i < sprites.Count; i++)
{
sprites[i].Update();
// 处理物体在边界上的碰撞,以后会通过引擎中的碰撞检测实现
if (sprites[i].Body.Position.X > (800.0f - sprites[i].Width / 2) || sprites[i].Body.Position.X < sprites[i].Width / 2)
{
sprites[i].Body.LinearVelocity *= new Vector2(-1, 1);
}
if (sprites[i].Body.Position.Y > (480.0f - sprites[i].Height / 2) || sprites[i].Body.Position.Y < sprites[i].Height / 2)
{
sprites[i].Body.LinearVelocity *= new Vector2(1, -1);
}
}
line.X1 = ball0.Body.Position.X;
line.Y1 = ball0.Body.Position.Y;
line.X2 = mouseX;
line.Y2 = mouseY;
if (totalTime > 1)
{
txtFps.Text = "Fps:" + fps.ToString();
totalTime = 0;
fps = 0;
}
// 保存当前时刻
LastTick = DateTime.Now;
}
private void btnStart_Click(object sender, System.Windows.RoutedEventArgs e)
{
if (!isRunning)
{
btnStart.Content = "暂停";
// 保存当前时刻
LastTick = DateTime.Now;
CompositionTarget.Rendering += new EventHandler(CompositionTarget_Rendering);
this.KeyUp += new KeyEventHandler(Page_KeyUp);
this.MouseMove += new MouseEventHandler(MainPage_MouseMove);
this.MouseLeftButtonDown += new MouseButtonEventHandler(MainPage_MouseLeftButtonDown);
isRunning = true;
}
else
{
btnStart.Content = "继续";
CompositionTarget.Rendering -= new EventHandler(CompositionTarget_Rendering);
this.KeyUp -= new KeyEventHandler(Page_KeyUp);
this.MouseMove -= new MouseEventHandler(MainPage_MouseMove);
this.MouseLeftButtonDown -= new MouseButtonEventHandler(MainPage_MouseLeftButtonDown);
isRunning = false;
}
}
///
/// 光标移动时获取坐标
///
void MainPage_MouseMove(object sender, MouseEventArgs e)
{
mouseX = e.GetPosition(LayoutRoot).X;
mouseY = e.GetPosition(LayoutRoot).Y;
}
///
/// 点击鼠标后根据光标的位置设置小球的初速度
///
///
///
void MainPage_MouseLeftButtonDown(object sender, MouseButtonEventArgs e)
{
Vector2 velocity = new Vector2((float)mouseX - ball0.Body.Position.X, (float)mouseY - ball0.Body.Position.Y);
ball0.Body.LinearVelocity = velocity;
}
private void Page_KeyUp(object sender, KeyEventArgs e)
{
// 按1键切换小球的动摩擦因数
if(e.Key == Key.D1)
{
if (ball0.Body.Friction == 0.2f)
{
// 设置小球的阻尼系数
foreach (SphereSprite s in sprites)
{
s.Body.Friction = 0;
}
txtFriction.Text = sTxtFriction + "0";
}
else {
// 设置小球的阻尼系数
foreach (SphereSprite s in sprites)
{
s.Body.Friction = 0.2f;
}
txtFriction.Text = sTxtFriction + "0.2";
}
}
// 按2键切换小球的弹性系数
if (e.Key == Key.D2)
{
if (ball0.Body.Restitution == 1f)
{
// 设置小球的阻尼系数
foreach (SphereSprite s in sprites)
{
s.Body.Restitution = 0.5f;
}
txtRestitution.Text = sTxtRestitution + "0.5";
}
else
{
// 设置小球的阻尼系数
foreach (SphereSprite s in sprites)
{
s.Body.Restitution = 1f;
}
txtRestitution.Text = sTxtRestitution + "1";
}
}
}
}
}
主要就是模拟斯诺克台球在屏幕上放置小球。点击鼠标可以发射白球,速度大小是由白球和光标间的距离决定的。你可以设置小球的动摩擦因数和恢复系数看一下效果有什么不同,当动摩擦因数为0时,小球不会发生转动。
文件下载(已下载 1133 次)
发布时间:2011/7/12 下午4:15:04 阅读次数:9089
