9．碰撞1——光滑均匀小球间的碰撞

在引擎中实现了碰撞效果定会使人留下深刻的印象，但这是一个很难的部分，要实现完美的碰撞效果非常不容易，你需要在精度和速度之间找到平衡点。通常碰撞分为两部分：碰撞检测和碰撞反应，碰撞检测是数学几何问题，需要判断是否发生碰撞、在何时何处发生碰撞，很难！网上有很多大部头的书专门讲解碰撞检测背后的数学原理，本人推荐《Real-Time Collision Detection》，在本网站有下载电子书。而碰撞反应主要是物理问题，相对而言简单得多，主要解决碰撞后物体的运动情况。

真实碰撞情况是非常复杂的，本文讨论最简单的情况：两个光滑的、质量分布均匀的小球之间的碰撞。两个小球之间的碰撞只有一个接触点，且相互作用力的方向必为球心连线，而且因为质量分布均匀，质心即球心，即相互作用力的方向必为质心连线，这称之为“中心碰撞”。因为小球光滑，所以无需考虑接触点切线方向的作用力，也就无需计算接触点的坐标，而且没有切线方向的作用力，所以小球也不会发生旋转。

在发布这篇文章之前，我也整理了两篇文章：一篇为11.3.2 两个轴上的动量守恒，此篇文章介绍了在flash中实现球体非对心碰撞的方法；另一篇为8.1 线性碰撞，介绍了在silverlight中实现球体对心碰撞的方法。两篇文章的共同点是使用的都是最简单的碰撞检测方法，本文使用的也是这种方法，两篇文章还实现了两球发生完全弹性碰撞时的碰撞反应，而本文要介绍更通用的方法，可以同时处理完全弹性碰撞、完全弹性碰撞和非完全弹性碰撞。

首先我们讨论如何检测两个小球之间是否发生碰撞。

1．碰撞检测

前面已经提及，在这种最简单的情况下，我们无需计算接触点的坐标，只需判断是否发生碰撞，这还是非常简单的，如图1所示：

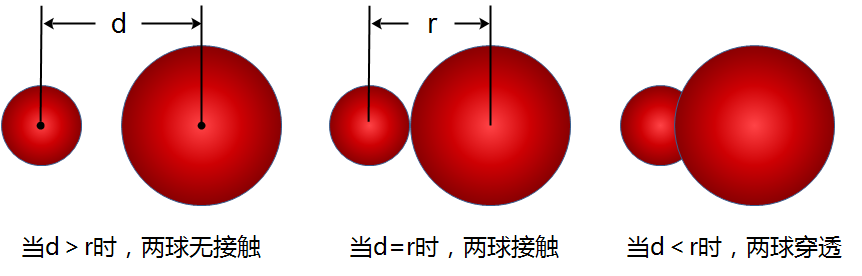
图1 两个球体之间的碰撞检测

我们首先计算两个球体质心间的距离d和两球半径之和r，然后判断d和r的大小关系得出是否发生接触，但是这只是发生碰撞的必要条件并不充分，还需要检查物体间的法向速度，以判断两物体是靠近中还是远离中，在代码中可以通过点乘相对速度和法线，然后从结果的正负情况进行判断。总而言之，碰撞发生的条件是物体正在接触且接触点朝对方移动，即如上中图所示，即使d＝r，若左球相对于右球的速度是向左的，仍然不会发生碰撞。

从上右图我们可以看到还会发生穿透现象，这会使模拟结果很不真实，这时就要使用连续碰撞检测（CCD）将程序倒退一个时间间隔再计算一次，直到没有穿透情况或者正好发生碰撞的情形。这个很难，本文不会介绍也不会现在在代码中实现，在小球速度不大的情况下几乎不会发生穿透现象。

代码实现

理解了原理，下面就讨论一下代码的实现。在World类的Step方法中的Slove方法后面添加以下代码：

public void Step(float dt)
{
    […] 
    // 对速度进行积分运算, 然后对位置进行积分计算。
    Solve(dt);
    
    // 遍历所有Body对象实现碰撞效果
    for (int i = 0; i < BodyList.Count - 1; i++)
    {
        Body body1 = BodyList[i]; 
        for (int j = i + 1; j < BodyList.Count; j++)
        {
            Body body2 = BodyList[j]; 
            
            SolveCollision(body1, body2);
        }
    }
    […]
}

为什么需要两个循环体的道理可以参见9.4 多物体碰撞检测策略。

而SolveCollision方法的代码如下：

#region 碰撞检测临时变量

float r;   // 两球半径之和
float d2; // 两球球心间距离平方
Vector2 normal; // 碰撞法线矢量
float vrn; // 相对速度的法线分量

#endregion

private void SolveCollision(Body body1, Body body2)
{
    // 计算两球的半径之和
    r = body1.Radius + body2.Radius;
    // 计算两球心间距离的平方
    d2 = (body1.Position.X - body2.Position.X) * (body1.Position.X - body2.Position.X) + (body1.Position.Y - body2.Position.Y) * osition.Y - body2.Position.Y);
    // 通过比较d平方和r平方判断是否发生碰撞。这里没有使用d.Length()和r比较，因为计算d的大小涉及开方操作比较耗费资源。
    bool isTouching = d2 <= r * r ? true : false; 
    
    // 计算球1质心指向球2质心的矢量，即法线矢量。normal=body2.Sweep.C.X - body1.Sweep.C.X的内联写法 
    normal.X = body2.Sweep.C.X - body1.Sweep.C.X; 
    normal.Y = body2.Sweep.C.Y - body1.Sweep.C.Y; 
    // 以下三行代码对法线normal进行归一化，即法线的单位向量。normal.Normalize()的内联写法。
    float factor = 1f / (float)Math.Sqrt(normal.X*normal.X+normal.Y*normal.Y); 
    normal.X *= factor; 
    normal.Y *= factor;
    
    // 计算相对速度的法线分量。Vector2.Dot (body1.LinearVelocityInternal - body2.LinearVelocityInternal,normal)的内联写法。
    // 数学知识告诉我们：这个值为正表示相对法线速度方向与法线方向的夹角小于90度，即两球正在相互靠近
    vrn = normal.X * (body1.LinearVelocityInternal.X - body2.LinearVelocityInternal.X) + normal.Y * (body1.LinearVelocityInternal.Y - body2.LinearVelocityInternal.Y);
    
    // 若d小于等于r且正在相互靠近则说明发生碰撞 
    if (isTouching && vrn > 0) 
    {
         // 碰撞反应代码，在后面实现
     }
}

2.碰撞反应

当上述碰撞检测过程检测到发生碰撞后，我们就要着手处理碰撞后物体的运动情况，这个问题主要是根据物理学中的动量守恒定律加以解决的。

2.1 动量守恒定律

如果一个系统不受外力或所受外力的矢量和为零，那么这个系统的总动量保持不变，这个结论叫做动量守恒定律。动量守恒定律是自然界中最重要最普遍的守恒定律之一，它既适用于宏观物体，也适用于微观粒子；既适用于低速运动物体，也适用于高速运动物体，它是一个实验规律，也可用牛顿第三定律和动量定理推导出来。

动量守恒定律和能量守恒定律以及角动量守恒定律一起成为现代物理学中的三大基本守恒定律。最初它们是牛顿定律的推论，但后来发现它们的适用范围远远广于牛顿定律，是比牛顿定律更基础的物理规律，是时空性质的反映。其中，动量守恒定律由空间平移不变性推出，能量守恒定律由时间平移不变性推出，而角动量守恒定律则由空间的旋转对称性推出。

在任何短暂的碰撞过程中，与相碰物体间巨大的内力相比，外力的冲量是微不足道的。因而总可认为，碰撞过程中系统的总动量是守恒的。

根据动量守恒定律，已知碰撞前两物体的初始条件，就可以求出碰撞后两物体的运动情况。

在无摩擦力的碰撞中，撞击的作用线垂直于碰撞的接触面。当速度沿作用线时，这种碰撞称为“直接碰撞”（direct impact）；当作用线通过物体质心时，这种碰撞称为“中心碰撞”（central impact）。质量分布均匀的球体遭受的撞击都是中心碰撞，而直接中心碰撞发生在作用线通过碰撞物体质心且速度沿着作用线时，对应的就是一维直线上的碰撞。当物体的速度不沿着作用线时，这种撞击称为“倾斜碰撞”(oblique impact)，在这种情况中你可以利用分解速度来分析倾斜碰撞，只有平行于作用线的分量才与碰撞有关，而垂直于作用线的分量则无，对应的是二维平面上的碰撞。图2显示了这些碰撞。

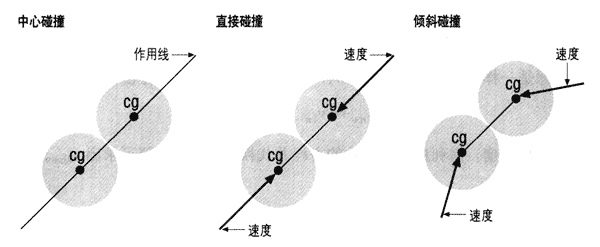
图2 撞击的种类

以上公式对应的都是一维直线上的碰撞，如果处理的二维平面，速度应该代矢量形式。

例如如图3所示有两个质量分布均匀的球体，一个质量m₁＝1kg，初速度v₁₀＝1m/s向右，另一个质量为m₂＝2kg，初速v₂₀＝2m/s向左，从图中可以看出这属于前面提到的直接中心碰撞，碰撞只发生在球心连线上。那么如何计算它们发生碰撞后的速度v₁和v₂？

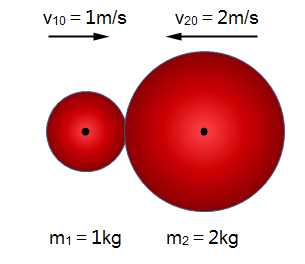
图3 两个小球的直接中心碰撞

根据能量损耗的情况主要分为三种情况。

2.1.1 完全非弹性碰撞

若在碰撞过程中相对动能完全耗散掉，碰撞后两物体不再分离，这种情况称之为完全非弹性碰撞。根据动量守恒定律（设向右为正）：

m₁v₁₀＋m₂v₂₀＝（m1＋m2）v_共

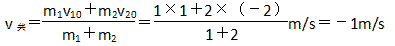
即碰撞后两者黏在一起以1m/s的速度向左运动。

2.1.2 完全弹性碰撞

若在碰撞过程中没有能量损耗，这种情况称之为完全弹性碰撞。需要动量守恒定律和动能守恒联立才能解出方程：

m₁v₁₀＋m₂v₂₀＝m₁v₁＋m₂v₂

以上两式联立解得：

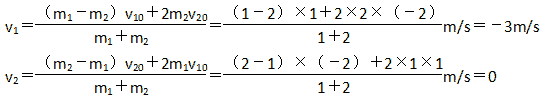
即m₁小球以3m/s的速度反弹，m₂小球恰静止。

2.1.3 非完全弹性碰撞

若碰撞过程中相对动能只耗散掉一部分，这种情况称之为非完全弹性碰撞，要解出方程，还需要一个由两碰撞物体的材质、结构、几何形状等决定的物理量：恢复系数e（coefficient of restitution），定义为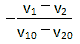 ，这个恢复系数可由实验测出，范围为[0,1]，当e＝0时即完全非弹性碰撞，e＝1时为完全弹性碰撞。下表为几种材料的恢复系数。

有了恢复系数，则碰撞后的速度v1和v2可由以下公式计算，若取e＝0.5，则：

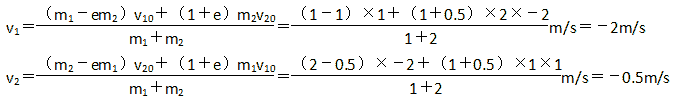
即碰撞后m₁和m₂小球都向左运动。

上述公式可以同时处理以上三种碰撞情况，当e＝0退化为完全非弹性碰撞，e＝1退化为完全弹性碰撞。

2.2 线性冲量

如果要解决球体的碰撞反应，使用上述的动量守恒定律和恢复系数就够用了，但是如果碰撞物体是不规则的的刚体，则需要用到更全面的方法。这种方法要计算碰撞物体间的线性冲量（本文不涉及角冲量的计算），然后将此线性冲量作用在物体上改变其速度。施加线性冲量的代码前面的文章已经实现了，只需通过物理公式的推导线性冲量的公式，此公式的推导过程较复杂，就不列出了，可参见《游戏开发物理学》第101-102页。我们只需知道结论，碰撞后施加在两物体上的冲量I矢量为：

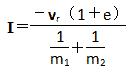
式中v_r为第一个刚体（注意：这个方法不仅可以用在小球的情况下，也可以用在不规则的刚体上）相对于第二个刚体的速度矢量。 有了作用在物体上的冲量，则可以用以下公式计算两个刚体碰撞之后的速度：

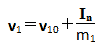
因为碰撞时作用在两个物体上的冲量大小相等，方向相反且在一直线上，所以：

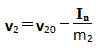
公式中的I_n为法线方向的冲量矢量。

下面我们根据这个通用方法将上面的非完全弹性碰撞的例子再做一遍。这个例子是一维直线上的碰撞，因此上述矢量式可以简化为标量式。首先计算相对速度

v_r＝v₁₀－v₂₀＝1－（－2）＝3m/s

然后计算冲量：

I＝－3×（1＋0.5）/（1＋0.5）＝－3N•s

两刚体的最后的速度为：

v₁＝1＋－3/1＝－2m/s

v₂＝－2＋3/2＝－0.5m/s

结果完全相同！但这种方法更为通用。

2.3 倾斜碰撞

前面讨论的例子只处理了一维直线上的碰撞情况，下面我们将讨论如果处理倾斜碰撞，如下图4所示，质量为2kg，半径为2m/s的小球1以5m/s的速度向上运动，质量为3kg，半径为3m的小球2以5m/s的速度向左运动，如何求出这种情况下的两个小球末速度？

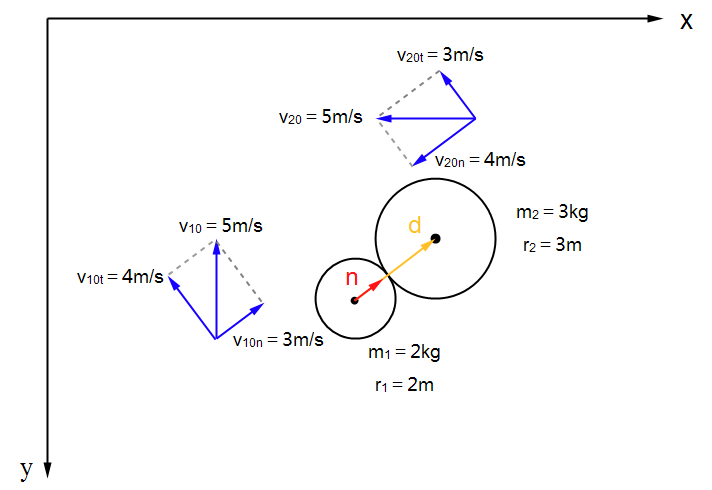
图4 两个小球的倾斜碰撞

首先我们需要求出碰撞的法线方向，这个方向就是小球1球心指向小球2球心的方向，图4用黄色箭头d表示，d的矢量表达式为d＝4i－3j（i和j表示x与y方向上的单位矢量），然后对它归一化，获取单位法线向量（用红色箭头表示）n＝0.8i－0.6j。然后获取v₁₀和v₂₀的法线分量v_10n＝3m/s和v_20n＝－4m/s，做好准备工作后，就可以按前面提到的公式计算法线方向的碰撞结果了，设e＝1，则：

v_rn＝v_10n－v_20n＝7m/s

I_n＝－7×（1＋1）/（0.5＋1/3）＝－16.8N•s

v_1n＝3－16.8/2＝－5.4m/s

v_2n＝－4＋16.8/3＝1.6m/s

而小球在切线方向的速度v_10t和v_20t保持不变，因此小球的最终速度大小为：

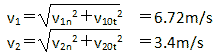
速度方向也可以求出，不再赘述。

2.4 代码实现

理解了上述原理，就可以编写碰撞反应代码了，完整代码如下：

#region 碰撞检测临时变量

float r;   // 两球半径之和
float d2; // 两球球心间距离平方
Vector2 normal; // 碰撞法线矢量
float normalImpulse; // 法线方向的冲量
float normalMass; // 计算法线冲量时用到的等效质量
float vrn; // 相对速度的法线分量
float restitution; // 恢复系数

#endregion

private void SolveCollision(Body body1, Body body2)
{
    // 计算两球的半径之和
    r = body1.Radius + body2.Radius;
    // 计算两球心间距离的平方
    d2 = (body1.Position.X - body2.Position.X) * (body1.Position.X - body2.Position.X) + (body1.Position.Y - body2.Position.Y) * osition.Y - body2.Position.Y);
    // 通过比较d平方和r平方判断是否发生碰撞。这里没有使用d.Length()和r比较，因为计算d的大小涉及开方操作比较耗费资源。
    bool isTouching = d2 <= r * r ? true : false; 
    
    // 计算球1质心指向球2质心的矢量，即法线矢量。normal=body2.Sweep.C.X - body1.Sweep.C.X的内联写法 
    normal.X = body2.Sweep.C.X - body1.Sweep.C.X; 
    normal.Y = body2.Sweep.C.Y - body1.Sweep.C.Y; 
    // 以下三行代码对法线normal进行归一化，即法线的单位向量。normal.Normalize()的内联写法。
    float factor = 1f / (float)Math.Sqrt(normal.X*normal.X+normal.Y*normal.Y); 
    normal.X *= factor; 
    normal.Y *= factor;
    
    // 计算相对速度的法线分量。Vector2.Dot (body1.LinearVelocityInternal - body2.LinearVelocityInternal,normal)的内联写法。
    // 数学知识告诉我们：这个值为正表示相对法线速度方向与法线方向的夹角小于90度，即两球正在相互靠近
    vrn = normal.X * (body1.LinearVelocityInternal.X - body2.LinearVelocityInternal.X) + normal.Y * (body1.LinearVelocityInternal.Y - body2.LinearVelocityInternal.Y);
    
    // 若d小于等于r且正在相互靠近则说明发生碰撞 
    if (isTouching && vrn > 0) 
    {
         // 碰撞时受到的冲量的公式为：
         // I＝－vr(1+e)/(1/m1＋1/m2) 
         // 可将1/(1/m1＋1/m2)看成一个等效质量
         normalMass normalMass = 1.0f / (body1.InvMass + body2.InvMass); 
         // 恢复系数取为两个球体恢复系数的平均值
         restitution = (body1.Restitution + body2.Restitution) / 2; 
         // 更据公式计算法线冲量
         normalImpulse = -normalMass * vrn * (1+restitution ); 
         // 分别求出x,y方向上的冲量分量 
         float Ix = normalImpulse * normal.X;
         float Iy = normalImpulse * normal.Y;
         
         // 在两个刚体上施加冲量
         body1.LinearVelocityInternal.X += body1.InvMass * Ix; 
         body1.LinearVelocityInternal.Y += body1.InvMass * Iy; 
         body2.LinearVelocityInternal.X -= body2.InvMass * Ix; 
         body2.LinearVelocityInternal.Y -= body2.InvMass * Iy; 
     }
}

其中恢复系数Restitution是在Body类中新添的一个属性。但是从物理上来说这是不正确的，因为恢复系数是碰撞的两个物体共同的属性，讨论一个物体的恢复系数是无意义的。但在计算机代码上只能这样做，我进行的操作是取两者的平均值，你也可以取个较大值或取个较小值。

其余原理在源代码的注释中已经写得很清楚了。

Silverlight示例

示例的代码就不贴了，自己看源代码吧。 在屏幕上添加了15个小球，随机赋予半径、初速和恢复系数。如果每个小球的恢复系数为1的话，则系统总动能不变，小球会永远不停地动下去，而这个例子中小球最终会停下来。

发布时间：2011/7/8 下午9:03:34  阅读次数：12873