7．刚体动力学

在前一篇文章中，我们直接设置了刚体的角速度和角加速度让它进行旋转，现在的问题是：刚体的角加速度究竟是由什么决定的？

物理知识

如下图所示，若外力F（图中的箭头表示）的作用线通过物体质心且刚体绕质心的初始角速度为零，则物体只做平动，可应用质心运动定理，建立刚体平动的动力学微分方程：

F_外＝ma＝mdv_C/dt

式中v_c为质心的运动速度矢量。

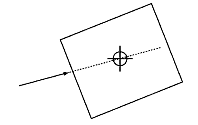
若如下图所示外力作用线不过质心O，刚体就要旋转，如果O是固定的，这在物理学上称为刚体定轴转动。

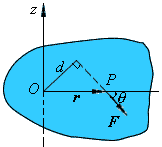
我们发现：在这个力的作用下，刚体的转动效果不仅与F的大小有关，还和F的作用线到转轴的距离有关，因此我们提出一个新的物理量——力矩（moment，torque），在高中物理中力矩定义为力与力臂的乘积，力臂的定义为力的作用线与转轴的距离，即图中的d。公式如下：

M＝Fd

在高中物理中不讨论力矩是否是矢量，只说明若假设顺时针力矩为正，则逆时针力矩取为负值，事实上是将力矩作为标量处理的。

但是大学物理告诉我们，力矩是一个矢量，它定义为转动轴到着力点的矢量与力矢量的叉乘，公式为：

M＝r×F         （公式1）

在右手坐标系中（即XNA使用的坐标系），M的方向是由右手螺旋定则进行判断的，即将右手拇指伸直，四指弯曲由r转向F，这时大拇指方向就是力矩的方向，上图中的力矩方向为竖直向下，即-z方向。若处理的是刚体定轴转动，那么力矩只有两个方向，这也是高中物理用带符号的标量表示力矩的原因。而在2D物理引擎中处理的也是这种情况，若你想要实现的是3D物理引擎，就需要讨论更复杂的刚体定点转动，目前还用不到。

在质点运动学中我们曾经讨论过：力F可以使质点产生加速度a，而物体的质量表示速度v改变的难易程度，公式为F＝ma。类似的情况有：在转动中，力矩M可以使刚体产生角加速度α，表示物体角速度ω改变难易程度的物理量叫做转动惯量I，所以刚体转动的动力学方程为：

M＝Iα＝Idω/dt

至于如何求物体的转动惯量，还是去翻大学物理书吧。

目前这个引擎要用到的是： 1．均匀矩形板以中心为转轴的转动惯量为m(a²＋b²)/12，其中m为板的质量，a、b分别为板长和板宽； 2．均匀薄圆盘，转轴为中心与盘面垂直的情况下，转动惯量为mR²/2，其中R为圆盘的半径。

若刚体内所有的运动点都平行于某一平面，则这种运动叫做刚体的平面平行运动。而2D物理引擎处理的就是这种运动。归纳起来，刚体平面平行运动可分解为质心的运动和绕质心的转动，二者的动力学方程分别为

质心运动定理：F_外＝ma＝mdv_C/dt

绕质心的转动：M＝Iα＝Idω/dt

故应用以上两个方程，即可建立刚体一般运动的微分方程。再利用欧拉运动学方程和初始条件，即可确定刚体在空间的一般运动规律。

在前面的质点动力学中，我们不仅讨论了牛顿定律，还讨论了适用范围更广的动量定理：I＝Ft＝Δp＝mΔv，在转动中也有对应的规律。与动量p对应的叫做角动量J，定义为J＝Iω（对应p＝mv）；与冲量I对应的叫做角冲量，又叫冲量矩，定义为Mt（对应I＝Ft），对应动量定理是角动量定理：

∫Mdt＝I(ω－ω₀)                （公式2）

即角冲量等于角动量的增量。

在Stun2Dphyisics中的实现

有了以上的物理知识，我们开始在引擎中添加新的代码。

1．在Body类中添加转动惯量

/// 

/// Body的转动惯量。 
/// 2D空间中的转动惯量是一个标量，表示body绕质心转动的难易程度。
/// 不同形状的物体转动惯量也不同。对于诸如圆、矩形之类的基本形状来说，有公式
/// 可以根据形状属性（圆半径或矩形的长宽）计算转动惯量。
/// 若Body不是基本形状，通常也可以使用接近的基本形状进行近似模拟。
/// 还可以使用更高级的算法计算非基本形状的转动惯量。
/// 
/// M转动惯量不能小于等于0
public float MomentOfInertia
{
    get { return momentOfInertia; }
    set
    {
        if (value <= 0)
            throw new ArgumentException("转动惯量不能为小于等于0", "value");

        momentOfInertia = value;

        if (isStatic)
            inverseMomentOfInertia = 0;
        else
            inverseMomentOfInertia = 1f / value;
    }
}

/// 

/// 转动惯量的倒数(1/)
/// 
public float InverseMomentOfInertia
{
    get { return inverseMomentOfInertia; }
}

额外设置一个转动惯量倒数的原因和设置一个质量倒数的原因是一样的。

2．添加工厂类自动创建Body

你可以手动创建一个Body，代码如下：

Body body=new Body();
Body.Mass=1; 
// 若Body为质量为1，长宽各为1的矩形，根据以上物理知识，它的转动惯量为
// 1*(12+12)/12=1/6
Body. MomentOfInertia=1/6; 

但是为了使用更方便，我们可以将这个计算公式整合到引擎中，所以在引擎项目中新建名为Factories的文件夹，在这个文件夹中新建一个名为BodyFactory.cs的类，代码如下：

namespace Stun2DPhysics4SL.Factories
{
    /// 

    /// 便于创建Body的工厂方法
    /// 
    public class BodyFactory
    {
        private static BodyFactory _instance;

        private BodyFactory()
        {
        }

        public static BodyFactory Instance
        {
            get
            {
                if (_instance == null)
                {
                    _instance = new BodyFactory();
                }
                return _instance;
            }
        }

        #region 矩形
        /// 

        /// 创建一个矩形Body。
        /// 
        /// 物理引擎。
        /// 矩形宽。
        /// 矩形高。
        /// 质量。
        /// 
        public Body CreateRectangleBody(PhysicsSimulator physicsSimulator, float width, float height, float mass)
        {
            Body body = CreateRectangleBody(width, height, mass);
            physicsSimulator.Add(body);
            return body;
        }

        /// 

        /// 创建一个矩形Body。
        /// 
        /// 矩形宽。
        /// 矩形高。
        /// 质量。
        /// 
        public Body CreateRectangleBody(float width, float height, float mass)
        {
            if (width <= 0)
                throw new ArgumentOutOfRangeException("width", "矩形宽必须大于0");

            if (height <= 0)
                throw new ArgumentOutOfRangeException("height", "矩形高必须大于0");

            if (mass <= 0)
                throw new ArgumentOutOfRangeException("mass", "质量必须大于0");

            Body body = new Body();
            body.Mass = mass;

            // 设置矩形的转动惯量。
            body.MomentOfInertia = mass * (width * width + height * height) / 12;
            return body;
        }
        #endregion

        #region 圆形
        /// 

        /// 创建一个圆形Body。
        /// 
        /// 物理引擎。
        /// 圆半径。
        /// 质量。
        /// 
        public Body CreateCircleBody(PhysicsSimulator physicsSimulator, float radius, float mass)
        {
            Body body = CreateCircleBody(radius, mass);
            physicsSimulator.Add(body);
            return body;
        }

        /// 

        /// 创建一个圆形Body。
        /// 
        /// 圆形半径。
        /// 质量。
        /// 
        public Body CreateCircleBody(float radius, float mass)
        {
            if (radius <= 0)
                throw new ArgumentOutOfRangeException("radius", "半径必须大于00");

            if (mass <= 0)
                throw new ArgumentOutOfRangeException("mass", "质量必须大于0");

            Body body = new Body();
            body.Mass = mass;

            // 设置圆形的转动惯量
            body.MomentOfInertia = .5f * mass * (float)Math.Pow(radius, 2f);
            return body;
        }
        #endregion        
    }
}

此代码中除了可以新建矩形Body，还可以创建圆形Body。

3．添加转动方法

首先在Body类中添加力矩变量：

private float torque;     // Body所受合力矩

/// <summary>
/// 在下一次更新时施加在Body上的合力矩。 
/// 在每次更新调用后都会清零，因此这个值必须在更新前被调用。 
/// 力矩可以看成是力的rotational analog。
/// 这个属性是只读的。
/// </summary>
/// 力矩。
public float Torque { get { return torque; } }

虽然力矩是一个矢量，但是在二维空间中只有两个方向，所以可以用一个浮点数表示力矩，而这个数的正负表示这两个方向。 然后移除角加速度变量AngularAcceleration = 0;，因为现在角加速度不是事先指定的，而是指定力矩在程序内部计算得出的。

下面在IntegrateVelocity方法中将代码：

dw = AngularAcceleration * dt; 

修改为：

dw = torque * inverseMomentOfInertia * dt; 

要让刚体转动，可以有三种方法，第一种方法是施加一个不过质心的力，代码如下：

#region ApplyForceAtLocalPoint临时变量
private Vector2 diff;
#endregion

/// <summary>
/// 在世界坐标系施加一个力，若这个力不过质点，则会施加力矩使刚体转动。 
/// </summary>
/// 力。 
/// 世界坐标系中的位置。
public void ApplyForceAtWorldPoint(Vector2 setForce, Vector2 point)
{
    Vector2.Subtract(ref point, ref position, out diff); 
    
    float _torque = diff.X * setForce.Y - diff.Y * setForce.X;
    
    // 施加力矩
    torque += _torque;
    
    // 施加力
    force.X += setForce.X;
    force.Y += setForce.Y; 
}

在上面的公式1中我们知道，力矩是物理知识我们力矩就是转动轴到着力点的矢量与力矢量的叉乘，因此转动轴到着力点的矢量r由上面的代码Vector2.Subtract(ref point, ref position, out diff);计算。

叉乘由代码float _torque = diff.X * setForce.Y - diff.Y * setForce.X;进行计算。

三维矢量叉乘的几何意义是获得垂直于这两个矢量所在平面的矢量，因此二维矢量叉乘没有几何意义（如果你看过XNA框架自带的Vector2结构，你会发现它并没有Vector3拥有的Cross方法），类似的定义是2D拟叉乘（pseudo cross product），2D拟叉乘返回的是一个标量，但这正好就是我们想要的结果，这个标量大于0表示顺时针旋转，小于0表示逆时针旋转。公式如下：

V1(x1, y1)×V2(x2, y2) = x1y2 – y1x2

这个公式对应的就是上面的计算机代码。在世界坐标系中施加力并不常用，我们往往更习惯将力施加在物体上的某点，即作用在本地坐标系上，这需要实现ApplyForceAtLocalPoint方法，需要设计坐标系的转换，要到以后才会实现。

第二种方法是直接设置力矩，代码如下：

/// <summary>
/// 在Body上施加一个力矩。
/// </summary>
/// 力矩。
public void ApplyTorque(float setTorque)
{
    torque += setTorque;
}

/// <summary>
/// 清除施加在Body上的力矩。
/// 在每次更新后都要调用这个方法。
/// </summary>
public void ClearTorque() 
{
    torque = 0; 
}

第三种方法是设置一个角冲量，代码如下：

 /// <summary>
/// 施加角冲量。
/// </summary>
/// 角冲量。
public void ApplyAngularImpulse(float setImpulse)
{
    AngularVelocity += setImpulse * inverseMomentOfInertia; 
}

物理原理是根据上面的公式2，角速度的改变量等于角冲量除以转动惯量。

4 . 在PhysicsSimulator.cs中添加清除力矩的方法

非常简单，只需在PhysicsSimulator.cs类的ApplyForces方法中添加这一行代码即可：

body.ClearTorque();

在Silverlight中的实现

因为自动创建Body的工厂类方法需要知道Body的质量、大小信息，所以需要在Sprite类中添加两个变量：

// Sprite长和宽
protected float width; 
protected float height; 

在SpritePhysics的构造函数中增加质量作为参数。

在Box1Sprite和Box2Sprite的重写方法CreateSpriteUC指定长和宽，以下是Box1Sprite类中CreateSpriteUC()方法的代码：

public override UserControl CreateSpriteUC()
{
    width = 64;
    height = 64;
    return new Box2();
}

最后在MainPage.xaml.cs中添加键盘控制代码：

private void Page_KeyUp(object sender, KeyEventArgs e)
{
    // 如果点击1键则在上面一个矩形左上角施加一个向右的力 
    if (e.Key == Key.D1 )
    {
        box1.Body.ApplyForceAtWorldPoint(new Vector2(9000, 0), new Vector2(32, 98));
        box1.Body.IsStatic = false;
    }
    // 如果点击2键，则在中间一个矩形上施加一个力矩
    if (e.Key == Key.D2 & previousKey != e.Key) 
    { 
        box2.Body.ApplyTorque(200000);
    }
    // 如果点击3键 
    if (e.Key == Key.D3 & previousKey != e.Key) 
    {
        box3.Body.ApplyAngularImpulse(3400); 
    }
}

如果点击键盘1键，则对上面一个矩形（质量为1kg）施加一个力，因为这个矩形的中心位于(64,120)，而这个力的作用点位于(32,98)，即这个矩形的左上角，方向为向右，大小为9000N，所有在这个力作用下，最上面一个矩形会既向右平抛，又顺时针翻滚。通常silverlight的帧频为60，即一帧时间为1/60秒，所以这个力会产生9000m/s²的加速度，在1/60内使物体获得150m/s的初速度，而此力对应的力矩为9000•32N·m＝288000N·m，而这个矩形的转动惯量为约683kg•m²，所以在1/60秒内使物体获得了约7rad/s的角速度。

若点击2，则直接对第二个矩形施加大小为200000N·m的力矩，使物体获得约5rad/s的角速度。

若点击3，则对最下面一个矩形施加大小为3333（即200000/60）的角冲量，也能使物体获得约5rad/s的角速度。

发布时间：2011/6/14 上午11:55:33  阅读次数：10791