6．刚体运动学

目前我们已经初步实现了质点的运动，质点是一个理想化模型，我们无需关心它的大小，因此也不需要处理它的旋转。如果在实际问题中必须涉及物体的转动及其形状和大小，我们就要采取另外的模型——刚体。

物理知识

在外力作用下,物体的形状和大小保持不变,而且内部各部分相对位置保持恒定（没有形变），这种理想物理模型称之为刚体。

刚体的基本运动可分为平动和转动。

（1）固联在刚体上的任一直线，在各时刻的位置始终保持彼此平行的运动，叫做平动（translation）

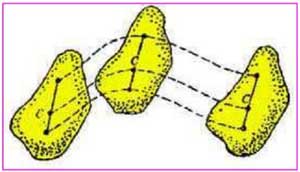
（2）刚体上所有各点都绕同一直线（转轴）做圆周运动，称为刚体的转动（rotation）。

刚体的一般运动可分解为平动和转动。如下图所示的手榴弹的抛体运动，手榴弹总是绕着一个本身的质心翻转，而质心在空中的轨道是一条抛物线（忽略阻力）。就是说，在手榴弹这一物体中，手榴弹在重力作用下运动的整体移动可以由质心的运动代表。

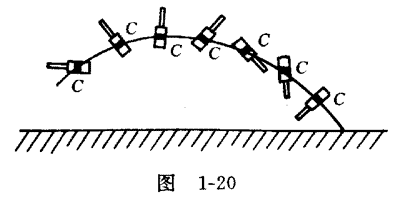
因此，刚体的平动完全可以由前面处理质点的代码处理，我们只需添加刚体转动的代码即可。

在研究质点平动时，我们需要指定三个物理量：位移s、速度v和加速度a，而速度可以通过加速度对时间的积分得出，位移可以通过速度对时间的积分得出。

在转动情况中，也有三个类似物理量：角位移θ，角速度ω和角加速度α。我们可以通过求角加速度对时间的积分求出角速度，公式如下：

ω＝∫ αdt

通过求角速度对时间的积分求出角位移，公式如下：

θ＝∫ ωdt

只需指定初始时刻的角加速度和角速度，我们就可以求出刚体在任意时刻的旋转量。

在Stun2DPhysics中的实现

由以上物理原理，我们需要在引擎中添加以下代码：

1． 在Body类中添加旋转相关的变量

public sealed class Body
{
    [..]
    private float previousAngularVelocity; // 上一次更新时的角速度
    private float previousRotation; // 上一次更新时的旋转量
    
    /// <summary>
    /// 获取或设置Body的角速度
    /// </summary>
    public float AngularVelocity;
    
    /// <summary>
    /// 获取或设置Body的角加速度
    /// </summary>
    public float AngularAcceleration = 0;
    
    internal float rotation; // 旋转量
    
    /// <summary>
    /// 获取或设置旋转量。
    /// </summary>
    public float Rotation
    {
        get { return rotation; }
        set { rotation = value;} 
    } 
    
    #region 积分运算临时变量
    private float dTheta; // 角位移改变量
    private float dw; // 角速度改变量 
    #endregion
    [..]
}

2．在IntegrateVelocity方法中添加计算角速度的代码

internal void IntegrateVelocity(float dt)
{
    [..]
    // 计算当前角速度
    dw = AngularAcceleration * dt; 
    previousAngularVelocity = AngularVelocity;
    AngularVelocity = previousAngularVelocity + dw;
}

3．在IntegratePosition方法中添加计算角位移的方法

/// 

/// 由引擎在内部调用，对位置进行积分运算。
/// 
/// 时间间隔</param>
internal void IntegratePosition(float dt){
    [..]
    /////////////////// 
    // 计算转动 // 
    ///////////////////
    
    // 角位移的改变量即角速度乘以时间
    dTheta = AngularVelocity * dt; 
    if(dTheta != 0f)
    {
        // 保存上一次更新时的旋转量
        previousRotation = rotation;
        // 计算当前旋转量 
        rotation = previousRotation + dTheta;
    }
}

在Silverlight中的使用

因为现在还需要处理UserControl的转动，所以需要在Sprite类和SpritePhysice类中添加处理旋转的代码，不是很难。

public abstract class Sprite
{
    [..]
    // 控件的旋转变换
    protected RotateTransform rotateTransform; 
    
    public Sprite(Canvas setCnvParent, Point initialLocation) 
    { 
        [..]
        // 设置控件的旋转变换
        rotateTransform = new RotateTransform(); 
        ucSpriteUC.RenderTransform = rotateTransform;
    }
}

public abstract class SpritePhysice : Sprite
{
    public override void Update()
    {
        [..] 
        rotateTransform.Angle = Body.Rotation * 180 / Math.PI; 
    }
}

在MainPage.xaml.cs修改了一些代码，实现了以下效果：将大矩形放置到屏幕左下角，当按下键盘A键时矩形做斜上抛运动，并且还会旋转。

在质点动力学中，我们问过：物体加速度是由什么决定的？答案是物体本身的质量和合外力，同样，刚体的角加速度是由什么决定的？答案是物体的转动惯量和合力矩，这将在下一篇文章——刚体动力学中加以讨论。

发布时间：2011/6/9 上午11:09:06  阅读次数：8501