2.3 热力学第一定律的建立

2.3.1 认识热的本质

热与分子运动联系紧密。我们现在知道，热其实就是大量分子无规则运动的结果。但是在历史上，对于热的本质却有两种对立的观点，一种是把热看成某种特殊物质（热质），叫热质说；另一种是把热看成物体内部分子的运动，叫运动说，后来逐步形成为分子动理论。两种观点进行过长期的争论。为了鉴别这两种观点孰是孰非，人们开展了大量实验研究和理论思考。可以说，热学早期发展史的一条主线就是如何科学地认识热的本质。在 18 世纪末到 19 世纪中叶，科学家从三个方面对热质说作出了明确的否决，热学才逐渐形成严密的理论体系。在这个体系中，占有特殊地位的就是大家所熟知的能量转化与守恒定律，这个定律在热学中也叫热力学第一定律。

18 世纪，热质说之所以兴盛是因为它能成功地解释量热学实验，而分子动理论却只能定性地说明少数热学现象，当时大多数物理学家都相信热质说。然而热质说毕竟似是而非，人们只要联系到更多的现象，认真地加以思考，就会看出其中的漏洞，甚至可以发现这是一个十分荒唐的理论。

首先，关于热质是否具有重量的问题，引起了人们的怀疑。

伦福德伯爵（Count Rumford，原名本杰明·汤普森，Benjamin Thompson，1753—1814）对热的本质作过周密的考查。他为了驳斥热质说，在1799 年公布了他做过的一个实验，这个实验的目的是测量“热质的重量”，看看一定重量的物质在温度变化前后重量有何变化。他用三个完全一样的瓶子分别装有等量的水、酒精和水银，放在一间恒温（16 ℃）的大房间内，搁置 24 小时后，用当时欧洲最精密的天平（灵敏度达百万分之一）来称重量。为了保证三个瓶子重量严格相等，他在较轻的瓶颈上挂一小段极细的银丝。然后将三个瓶子都移到 0℃ 的房子里，保持完全静止不受扰动，48 小时后再称其重量，结果是重量丝毫也没有变化，这时水已结成了冰。再将瓶子移回温室，即使冰又化成了水，重量仍无变化。伦福德宣称，他证明了热对物体的重量没有任何影响。

当然，伦福德仅仅靠热与重量无关的实验还不足以否定热质的存在，因为热质说者还可以假设热质不具重量就可以解释这个事实。伦福德接着又叙述了一个实验，无可辩驳地证明热质说的荒谬。

1797 年，伦福德在德国一家兵工厂监制大炮镗孔，他注意到铜炮被钻削时会产生大量的热，切下的铜屑更热，用水冷却，竟可使水立即沸腾。

这个现象其实不稀罕，摩擦生热自古尽人皆知。热质说者对这个现象也作了自圆其说的解释，说是因为物体在摩擦时，热质被拉曳，金属屑在从金属块中切削下来时带去了大量热质，因此显得特别热。伦福德爱好思索、喜欢钻研，他从年轻时代起就对热学中的疑难问题十分关心。他亲自做过许多热学实验，早就对热质这一套说法产生了怀疑，为了要从根本上作出判决，他就作了如下几个实验。

伦福德先比较金属屑和金属片的比热，从量热实验判定：它们的比热是一样的，于是就驳斥了热质说的金属屑比热大的论点。

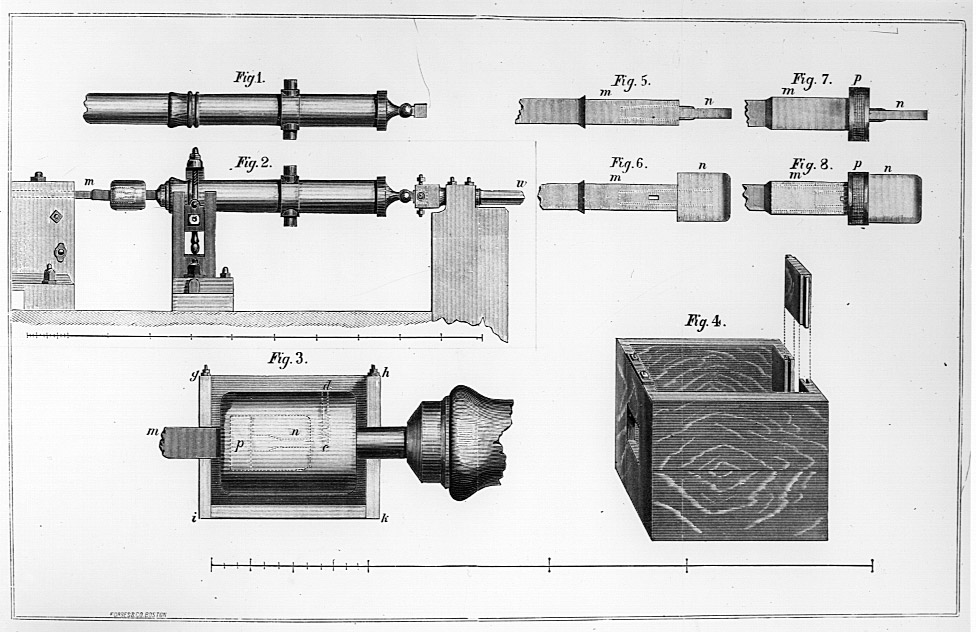
接着，伦福德做了一个专门设计的大炮钻孔实验，如图 2 – 13。他取一只重约 113 磅（约 51 公斤）的圆简铸件，放在钻孔机上，故意拿已经磨钝了的钻头钻孔，经过 30 分钟，铸件温度从 16℃ 升到 55℃。他在炮孔里共收集到切削下来的金属屑约 54 克，只占圆筒的 1/944。

伦福德问道：难道炮筒升温 39℃ 所需的热质是金属屑提供的吗？如果是这样，那么金属屑要降温 3.7 万度才能达到上述情况。

伦福德又做了一个水箱实验。他把圆筒放在一只水箱中，水重 18.77 磅（即 8.5 公斤），让马带动钝钻头在圆筒中旋转，经过 2 个半小时竟使水沸腾了。周围的观众人人都惊讶起来。这么多的水不用火烧，居然能沸腾，真是个奇迹。伦福德自己也简直无法抑制自己的喜悦心情。

伦福德想：这些热量从哪里来的？从金属切削的微粒里来的吗？事实证明不可能。从空气里来的吗？也不可能！因为有的实验是在水箱中做的，和空气隔离。从水里来的吗？更不对！水本身也热了，而且也没有发生任何化学变化。既不是空气，又不是水，只要继续摩擦，热会源源不断地产生，永无止境。那就证明，热的来源不是别的，而是运动。

1798 年 1 月 25 日伦福德在英国皇家学会宣读他的论文，文中写道：

“最近我应约去慕尼黑兵工厂领导钻制大炮的工作。我发现，铜炮在钻了很短的一段时间后，就会产生大量的热；而被钻头从大炮上钻下来的铜屑更热（像我用实验所证实的，发现它们比沸水还要热）。”

伦福德分析这些热是由于摩擦产生的，他说：“……我们一定不能忘记……在这些实验中，由摩擦所生的热的来源似乎是无穷无尽的。”[1]

伦福德的报告在 1798 年发表，立即得到英国化学家戴维（Humphry Davy，1778—1829）的响应。戴维也对热质说持怀疑态度。他在 1799 年发表了自己的摩擦生热的实验，并且致力于宣传热的运动说。

戴维所描述的实验考虑得非常周到。其中有一个是把两块温度为 – 2℃ 的冰，固定在由时钟改装的机构上，使两块冰不停地互相摩擦。整个装置放在大玻璃罩内再抽成真空。经过几分钟的剧烈摩擦，冰几乎全化成了水，温度达到 + 2℃。戴维根据这一类的实验论证说：热质是不存在的，摩擦和碰撞引起了物体内部微粒的特殊运动或振动，这种运动或振动就是热的本质。

伦福德和戴维的实验为热的运动说提供了有力的支持，成了建立能量转化与守恒定律的前奏。

19 世纪 40 年代以前，自然科学的发展为能量转化与守恒原理奠定了基础。除了在热学上对热的本质建立了正确的认识之外，还从以下几个方面做了准备。

1．力学方面的准备

机械能守恒是能量守恒定律在机械运动中的一个特殊情况。早在力学初步形成时就已有了能量守恒思想的萌芽。例如，伽利略研究斜面问题和摆的运动，斯梯芬研究杠杆原理，惠更斯研究完全弹性碰撞等都涉及能量守恒问题。17 世纪法国哲学家笛卡儿已经明确提出了运动不灭的思想。以后德国哲学家莱布尼茨引进活力的概念，首先提出活力守恒原理，他认为用 mv² 度量的活力在力学过程中是守恒的，宇宙间的“活力”的总和是守恒的。D．伯努利的流体运动方程（伯努利方程）实际上就是流体运动中的机械能守恒定律。

至 19 世纪 20 年代，力学的理论著作强调“功”的概念，把它定义成力对距离的积分，澄清了功和“活力”概念之间的数学关系，这就提供了一种机械“能”的度量，为能量转换建立了定量基础。1835 年哈密顿发表了《论动力学的普遍方法》一文，提出了哈密顿原理。至此能量守恒定律及其应用已经成为力学中的基本内容（参看 1.8 节）。

2．化学、生物学方面的准备

法国的拉瓦锡和拉普拉斯曾经用冰卡计测量物质在化学反应过程中所放出的热量以及物体燃烧或动物呼吸时所散发的热量。他们把燃烧物或待测动物放在冰卡计的内室中，如图 2 – 14 中的豚鼠。然后比较燃烧和动物呼吸所放出的热量与放出的二氧化碳之比，发现这两个比值近似相等。这个结果对能量转化与守恒定律的建立有重要意义，因为它启示了动物热的来源和呼吸的本质，从而为能量转化与守恒提供了不可多得的佐证。德国化学家莫尔（F．Mohr，1806—1879）从许多事例领悟到，不同形式的“力”（即能量）都是机械“力”的表现，他写道：

“除了 54 种化学元素外，自然界还有一种动因，叫做力。力在适当的条件下可以表现为运动、化学亲和力、凝聚、电、光、热和磁，从这些运动形式中的每一种可以得出一切其余形式。”

他明确地表述了运动不同形式的统一性和相互转化的可能性。

3．电磁学方面的准备

19 世纪二三十年代，随着电磁学基本规律的陆续发现，人们自然对电与磁、电与热、电与化学等关系密切注视。法拉第（Michael Faraday，1791—1867）尤其强调各种“自然力”的统一和转化，他认为“自然力”的转变，是其不灭性的结果。“自然力”不能从无生有，一种“力”的产生是另一种“力”消耗的结果。法拉第的许多工作都涉及转化现象，如电磁感应、电化学和光的磁效应等。他在 1845 年发表一篇讨论磁对光的作用的论文，表述了他对“力”的统一性和等价性的基本看法，他写道：

“物质的力所处的不同形式很明显有一个共同的起源，换句话说，是如此直接地联系着和互相依赖着，以至于可以互相转换，而在其行动中，力具有守恒性。”

正是在“力”的转化这一概念的基础上，法拉第做出了许多重要发现。

在电与热的关系方面，1821 年塞贝克（T．J．Seebeck）发现的温差电现象可以说是“自然力”互相转化的又一重要例证。后面还将提到，焦耳（J．P．Joule，1818—1889）在 1840 年研究电流的热效应中发现了 i²R 定律。这是反映能量转化的一个定量关系，对能量转化与守恒定律的建立有重要意义。

4．永动机的历史教训

永动机不可能实现的历史教训，从反面提供了能量守恒的例证。

2.3.2 能量转化与守恒定律初步形成

19 世纪初，由于蒸汽机的进一步发展，迫切需要对蒸汽机“出力”作出理论分析，因此，热与机械功的相互转化得到了广泛的研究。其中突出的事例有：

埃瓦特（Peter Ewart，1767—1842）对煤的燃烧所产生的热量和由此提供的“机械动力”之间的关系作了研究，建立了定量联系。

丹麦工程师和物理学家柯尔丁（L．Colding，1815—1888）对热、功之间的关系也作过研究。他从事过摩擦生热的实验，1843 年丹麦皇家科学院对他的论文签署了如下的批语：“柯尔丁的这篇论文的主要思想是由于摩擦、阻力、压力等造成的机械作用的损失，引起了物体内部的如热、电以及类似的动作，它们皆与损失的力成正比。”[2]

俄国的赫斯（G．H．Hess，1802—1850）比他们更早就从化学的研究得到了能量转化与守恒的思想。他原是瑞士人，3 岁时到俄国，当过医生，在彼得堡执教，以热化学研究著称。

1836 年赫斯向彼得堡科学院报告：“经过连续的研究，我确信，不管用什么方式完成化合，由此发出的热总是恒定的，这个原理是如此之明显，以至于如果我不认为已经被证明，也可以不假思索就认为它是一条公理。”[3]

在以后的岁月里，赫斯认识到上述原理的巨大意义，从各方面进行了实验验证，于1840 年 3 月 27 日在一次科学院演讲中提出了一个普遍的表述：“当组成任何一种化学化合物时，往往会同时放出热量，这热量不取决于化合是直接进行还是经过几道反应间接进行。”[4]以后他把这条定律广泛应用于他的热化学研究中。

赫斯的这一发现第一次反映了热力学第一定律的基本原理：热和功的总量与过程途径无关，只决定于体系的始末状态。它体现了系统的内能的基本性质与过程无关。这一定律不仅反映守恒的思想，也包括了“力”的转变思想。至此，能量转化与守恒定律已初步形成。

2.3.3 能量转化与守恒定律的确立

对能量转化与守恒定律作出明确叙述的，首先要提到三位科学家。他们是德国的迈尔（Robert Mayer，1814—1878）、赫姆霍兹（Hermann von Helmholtz，1821—1894）和英国的焦耳。

1．迈尔的工作

迈尔是一位医生。1840 年左右，迈尔作为随船医生前往印度尼西亚，在给生病的船员

放血时，得到了重要启示，发现静脉血不像生活在温带国家中的人那样颜色暗淡，而是像动脉血那样新鲜。当地医生告诉他，这种现象在辽阔的热带地区是到处可见的。他还听到海员们说，暴风雨时海水比较热。这些现象引起了迈尔的沉思。他想到，食物中含有化学能，它像机械能一样可以转化为热。在热带高温情况下，机体只需要吸收食物中较少的热量，所以机体中食物的燃烧过程减弱了，因此静脉血中留下了较多的氧。他已认识到生物体内能量的输入和输出是平衡的。

迈尔在 1842 年发表的题为《热的力学的几点说明》中，宣布了热和机械能的相当性和可转换性，他的推理如下：

“力是原因：因此，我们可以全面运用这样一条原则来看待它们，即‘因等于果’。设因 c 有果 e，则 c = e；反之，设 e 为另一果 f 之因，则有 e = f 等等，c = e = f = … = c。在一串因果之中，某一项或某一项的某一部分绝不会化为乌有，这从方程式的性质就可明显看出。这是所有原因的第一个特性，我们称之为不灭性。”

接着迈尔用反证法，证明守恒性（不灭性）：

“如果给定的原因 c 产生了等于其自身的结果 e，则此行为必将停止；c 变为 e；若在产生 e 后，c 仍保留全部或一部分，则必有进一步的结果，相当于留下的原因 c 的全部结果将大于 e，于是就将与前提 c = e 矛盾。”“相应地，由于 c 变为 e，e 变为 f 等等，我们必须把这些不同的值看成是同一客体出现时所呈现的不同形式。这种呈现不同形式的能力是所有原因的第二种基本特性。把这两种特性放在一起我们可以说，原因（在量上）是不灭的，而（在质上）是可转化的客体。”

迈尔的结论是：“因此力（即能量）是不灭的、可转化的、不可称量的客体。”[5]

迈尔这种推论方法显然过于笼统，难以令人信服，但他关于能量转化与守恒的叙述是最早的完整表达。

迈尔在 1845 年发表了第二篇论文：《有机运动及其与新陈代谢的联系》，该文更系统地阐明能量的转化与守恒的思想。他明确指出：“无不能生有，有不能变无”，“在死的和活的自然界中，这个力（按：即能量）永远处于循环转化的过程之中。任何地方，没有一个过程不是力的形式变化！”他主张：“热是一种力，它可以转变为机械效应。”[6]论文中还具体地论述了热和功的联系，推出了气体定压比热和定容比热之差 C_p – C_v 等于定压膨胀功 R 的关系式。现在我们称 C_p – C_v = R 为迈尔公式。

接着迈尔又根据狄拉洛希（Delaroche）和贝拉尔德（Berard）以及杜隆气体比热的实验数据 C_p = − 0.267卡/（克·度），C_v = 0.188卡/（克·度）计算出热功当量。

计算过程如下：

在定压下使 1 厘米³ 空气加热温升 1 度所需的热量为：Q_p = mc_pΔt = 0.000 347 卡（取空气密度 ρ = 0.0013克/厘米³）。相应地，在定容下加热同量空气温升 1 度消耗的热 Q_v = 0.000 244 卡。二者的热量差 C_p – C_v = 0.000 103 卡。另一方面，温度升高 1 度等压膨胀时体积增大为原体积的 1/274 倍；气体对外做的功，可以使 1.033 千克的水银柱升高 1/274 厘米。即

功 = 1.033×\(\frac{1}{{27400}}\) = 3.78×10⁻⁵ 千克·米。

于是迈尔得出热功当量为

J = \(\frac{A}{{{Q_p} - {Q_v}}}\) = \(\frac{{3.78 \times {{10}^{ - 5}}}}{{1.03 \times {{10}^{ - 7}}}}\) = 367 千克·米/千卡

或 3597 焦耳/千卡，现在的精确值为 4187 焦耳/千卡。

迈尔还具体地考察了另外几种不同形式的力。他以起电机为例说明了“机械效应向电的转化。”他认为：“下落的力”（即重力势能）可以用“重量和（下落）高度的乘积来量度。”“与下落的力转变为运动或者运动转变为下落的力无关，这个力或机械效应始终是不变的常量。”

迈尔第一个在科学史中将热力学观点用于研究有机世界中的现象，他考察了有机物的生命活动过程中的物理化学转变，确信“生命力”理论是荒诞无稽的。他证明生命过程无所谓“生命力”，而是一种化学过程，是由于吸收了氧和食物，转化为热。这样迈尔就将植物和动物的生命活动，从唯物主义的立场，看成是能的各种形式的转变。

1848 年迈尔发表了《天体力学》一书，书中解释陨石的发光是由于在大气中损失了动能。他还应用能量守恒原理解释了潮汐的涨落。

迈尔虽然第一个完整地提出了能量转化与守恒原理，但是在他的著作发表的几年内，不仅没有得到人们的重视，反而受到了一些著名物理学家的反对。由于他的思想不合当时流行的观念，不断遭到人们的诽谤和讥笑，使他在精神上受到很大刺激，曾一度关进精神病院，备受折磨。

2．赫姆霍兹的研究

从多方面论证能量转化与守恒定律的是德国的赫姆霍兹。他曾在著名的生理学家缪勒（Johannes Muller）的实验室里工作过多年，研究过“动物热”。他深信所有的生命现象都必得服从物理与化学规律。他早年在数学上有过良好的训练，同时又很熟悉力学的成就，读过牛顿、达朗贝尔、拉格朗日等人的著作，对拉格朗日的分析力学有深刻印象。他的父亲是一位哲学教授，和著名哲学家费赫特（Fichte）是好朋友。赫姆霍兹接受了前辈的影响，成了康德哲学的信徒，把自然界大统一当作自己的信条。他认为如果自然界的“力”（即能量）是守恒的，则所有的“力”都应和机械“力”具有相同的量纲，并可还原为机械“力”。1847 年，26 岁的赫姆霍兹写成了著名论文《力的守恒》，充分论述了这一命题。这篇论文原是 1847 年 7 月 23 日在柏林物理学会会议上的报告，由于被认为是思辨性、缺乏实验研究成果的一般论文，没有能够在当时有国际声望的《物理学年鉴》上发表，而是以小册子的形式单独印行。

但是历史证明，这篇论文在热力学的发展中占有重要地位，因为赫姆霍兹总结了许多人的工作，一举把能量概念从机械运动推广到了所有变化过程，并证明了普遍的能量守恒原理。这是一个十分有力的理论武器，从而可以更深入地理解自然界的统一性。

赫姆霍兹在这篇论文一开头就声称，他的“论文的主要内容是面对物理学家，”他的目的是“建立基本原理，并由基本原理出发引出各种推论，再与物理学不同分支的各种经验进行比较。”[7]

在他的论述中有一明显的趋向，就是企图把一切自然过程都归结于中心力的作用。大家知道，在只有中心力作用的条件下，能量总是守恒的，但是这只是能量守恒原理的一个特例，把中心力看成是普遍能量守恒的条件就不正确了。

他的论文共分六节，前两节主要是回顾力学的发展，强调了活力守恒（即动能守恒），进而分析了“力”的守恒原理（即机械能守恒原理）；第三节涉及守恒原理的各种应用；第四节题为“热的力当量性”。他明确地摒弃了热质说，把热看成粒子（分子或原子）运动能量的一种形式；第五节“电过程的力相当性”和第六节“磁和电磁现象的力相当性”讨论各种电磁现象和电化学过程。还特别以电池中的热现象为例对能量转化关系进行了详细研究。文章最后提到，能量概念也有可能应用于有机体的生命过程。他的论点和迈尔接近，不过，他当时可能并不知道迈尔的工作。

赫姆霍兹在结束语中写道：“通过上面的叙述已证明了我们所讨论的定律没有和任何一个迄今所知的自然科学事实相矛盾，反而却引人注目地为大多数事实所证实。……这定律的完全验证，也许必须看成是物理学最近将来的主要课题之一。”

实际上，验证这一定律的实验工作早在赫姆霍兹论文之前就已经开始了。焦耳在这方面做出了巨大贡献。

3．焦耳的实验研究

焦耳是英国著名实验物理学家。1818 年他出生于英国曼彻斯特市近郊，是富有的酿酒厂主的儿子。他从小在家由家庭教师教授，16 岁起与其兄弟一起到著名化学家道尔顿（John Dalton，1766—1844）那里学习，这在焦耳的一生中起了关键的指导作用，使他对科学发生了浓厚的兴趣，后来他就在家里做起了各种实验，成为一名业余科学家。

这时正值电磁力和电磁感应现象发现不久，电机当时叫磁电机（electric-magnetic engine）——刚刚出现，人们还不大了解电磁现象的内在规律，也缺乏对电路的深刻认识，只是感到磁电机非常新奇，有可能代替蒸汽机成为效率更高、管理方便的新动力，于是一股电气热潮席卷了欧洲，甚至波及美国。焦耳当时刚 20 岁，正处于敏感的年龄，家中又有很好的实验条件，他父亲厂里有蒸汽机，这使他对革新动力设备发生了兴趣，就投入到电气热潮之中，开始研究起磁电机来。

从 1838 年到 1842 年的几年中，焦耳一共写了八篇有关磁电机的通讯和论文，以及一篇关于电池、三篇关于电磁铁的论文。他通过磁电机的各种试验注意到电机和电路中的发热现象，他认为这和机件运转中的摩擦现象一样，都是动力损失的根源。于是他就开始进行电流热效应的研究。

1841 年他在《哲学杂志》上发表文章《电的金属导体产生的热和电解时电池组中的热》，叙述了他的实验：为了确定金属导线的热功率，让导线穿过一根玻璃管，再将它密缠在管上，每圈之间留有空隙，线圈终端分开。然后将玻璃管放入盛水的容器中，通电后用温度计测量水产生的温度变化。实验时，他先用不同尺寸的导线，继而又改变电流的强度，结果判定“在一定时间内伏打电流通过金属导体产生的热与电流强度的平方及导体电阻的乘积成正比。”这就是著名的焦耳定律，又称 i²R 定律。

随后，他又以电解质做了大量实验，证明上述结论依然正确。

i²R 定律的发现使焦耳对电路中电流的作用有了明确的认识。他仿照动物体中血液的循环，把电池比作心肺，把电流比作血液，指出：“电可以看成是携带、安排和转变化学热的一种重要媒介”，并且认为，在电池中“燃烧”一定量的化学“燃料”，在电路中（包括电池本身）就会发出相应大小的热，和这些燃料在氧气中点火直接燃烧所得应是一样多。请注意，这时焦耳已经用上了“转变化学热”一词，说明他已建立了能量转化的普遍概念，他对热、化学作用和电的等价性已有了明确的认识。

然而，这种等价性的最有力证据，莫过于热功当量的直接实验数据。正是由于探索磁电机中热的损耗，促使焦耳进行了大量的热功当量实验。1843 年焦耳在《磁电的热效应和热的机械值》一文中叙述了他的目的，写道：

“我相信理所当然的是：磁电机的电力与其他来源产生的电流一样，在整个电路中具有同样的热性质。当然，如果我们认为热不是物质，而是一种振动状态，就似乎没有理由认为它不能由一种简单的机械性质的作用所引起，例如像线圈在永久磁铁的两极间旋转的那种作用。与此同时，也必须承认，迄今尚未有实验能对这个非常有趣的问题作出判决，因为所有这些实验都只限于电路的局部，这就留下了疑问，究竟热是生成的，还是从感应出磁电流的线圈里转移出来的？如果热是线圈里转移出来的，线圈本身就要变冷。……所以，我决定致力于清除磁电热的不确定性。”

焦耳把磁电机放在作为量热器的水桶里，旋转磁电机，并将线圈的电流引到电流计中进行测量，同时测量水桶的水温变化。实验表明，磁电机线圈产生的热也与电流的平方成正比。焦耳又把磁电机作为负载接入电路，电路中另接一电池，以观察磁电机内部热的生成，这时，磁电机仍放在作为量热器的水桶里，焦耳继续写道：“我将轮子转向一方，就可使磁电机与电流反向而接；转向另一方，可以借磁电机增大电流。前一情况，仪器具有磁电机的所有特性；后一情况适得其反，它消耗了机械力。”

比较磁电机正反接入电路的实验，焦耳得出结论：“我们从磁电得到了一种媒介，用它可以凭借简单的机械方法，破坏热或产生热。”

至此，焦耳已经从磁电机这个具体问题的研究中领悟到了一个具有普遍意义的规律，这就是热和机械功可以互相转化，在转化过程中一定有当量关系。他写道：

“在证明了热可以用磁电机生成，用磁的感应力可以随意增减由于化学变化产生的热之后，探求热和得到的或失去的机械功之间是否存在一个恒定的比值，就成了十分有趣的课题。为此目的，只需要重复以前的一些实验并同时确定转动仪器所需的机械力。”[8]

焦耳在磁电机线圈的转轴上绕两条细线，相距约 27.4 米处置两个定滑轮，跨过滑轮挂有砝码，砝码约几磅重（1 磅 = 0.453 59 千克），可随意调整。线圈浸在量热器的水中，从温度计的读数变化可算出热量，从砝码的重量及下落的距离可算出机械功。在 1843 年的论文中，焦耳根据 13 组实验数据取平均值得如下结果：

“能使 1 磅的水温度升温华氏 1 度的热量等于（可转化为）把 838 磅重物提升 1 英尺的机械功。”

838 磅·英尺相当于 1135 焦耳，这里得到的热功当量 838磅·英尺/英热单位等于 4.511 焦耳/卡（现代公认值为 4.187 焦耳/卡）。

焦耳并没有忘记测定热功当量的实际意义，就在这篇论文中他指出，最重要的实际意义有两点：（1）可用于研究蒸汽机的出力；（2）可用于研究磁电机作为经济的动力的可行性。可见，焦耳研究这个问题始终没有离开他原先的目标。

焦耳还用多孔塞置于水的通道中，测量水通过多孔塞后的温升，得到热功当量为 770 磅·英尺/英热单位（4.145 焦耳/卡）。这是焦耳得到的与现代热功当量值最接近的数值。

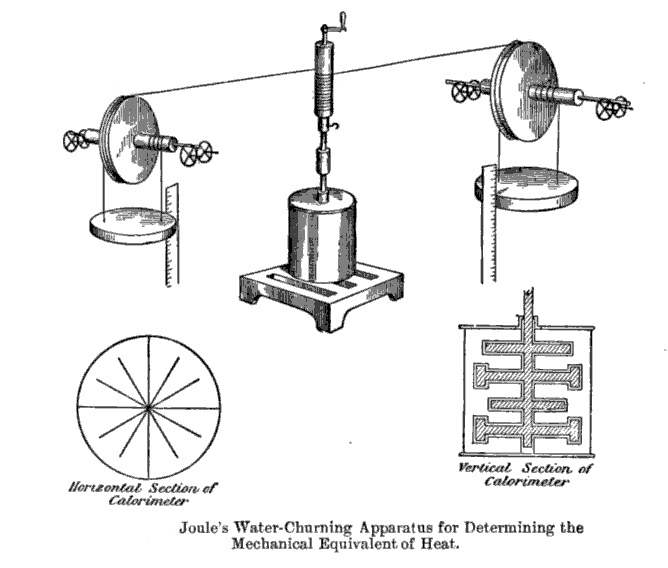
1845 年，焦耳报导他在量热器中安装一带桨叶的转轮，如图 2 – 19，经滑轮吊两重物下滑，桨轮旋转，不断搅动水使水升温，测得热功当量为 890 磅·英尺/英热单位，相当于 4.782 焦耳/卡。

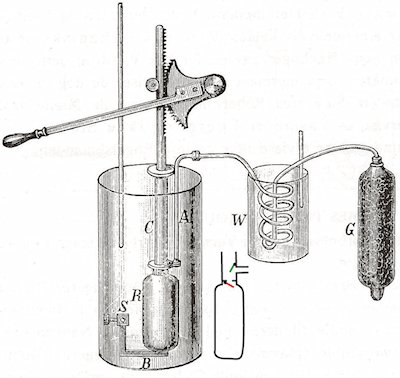
同年，焦耳写了论文《空气的稀释和浓缩所引起的温度变化》，记述了如下实验：把一个带有容器 R 的压气机 C 放在作为量热器的水桶 A 中，如图 2 – 21。压气机把经过干燥器 G 和蛇形管 W 的空气压缩到容器 R中，然后测量空气在压缩后的温升，从温升可算出热量。气压从一个大气压变为 22 个大气压，压缩过程视为绝热过程，可计算压气机做的功。由此得到热功当量为 823 及 795 磅·英尺/英热单位。然后，经蛇形管释放压缩空气（图 2 – 22），量热器温度下降，又可算出热功当量为 820、814、760 磅·英尺/英热单位，从空气的压缩和膨胀得到的平均值为 798 磅·英尺/英热单位，相当于 4.312 焦耳/卡。

1849 年 6 月，焦耳作了题为《热功当量》的总结报告[9]，全面整理了他几年来用桨叶搅拌法和铸铁摩擦法测热功当量的实验，给出如下结果（单位均以磅·英尺/英热单位表示）：

焦耳的实验结果处理得相当严密，在计算中甚至考虑到将重量还原为真空中的值。对上述结果，焦耳作了分析，认为铸铁摩擦时会有微粒磨损，要消耗一定的功以克服其内聚力，因此所得结果可能偏大。汞和铸铁在实验中不可避免会有振动，产生微弱的声音，也会使结果偏大。在这三种材料中，以水的比热最大，所以比较起来，应该是用水做实验最准确。因此，在他的论文结束时，取 772 磅·英尺/英热单位作为最后结果，这相当于4.154 焦耳/卡。对此，他概括出两点：

“第一，由物体，不论是固体或液体，摩擦产生的热量总是正比于消耗的力之量；

第二，使 1 磅水（在真空中称量，用于 55 ℉ ~ 60 ℉）的温度升高 1 ℉，所需消耗的机械力相当于 772 磅（物体）下落 1 英尺。”

焦耳从 1843 年以磁电机为对象开始测量热功当量，直到 1878 年最后一次发表实验结果，先后做实验不下四百余次，采用了原理不同的各种方法，他以日益精确的数据，为热和功的相当性提供了可靠的证据，使能量转化与守恒定律确立在牢固的实验基础之上。

4．全面的表述

能量转化与守恒定律是自然界基本规律之一。恩格斯对这一规律的发现给予崇高的评价，把它和达尔文进化论及细胞学说并列为三大自然发现。能量转化与守恒定律这个全面的名称就是恩格斯首先提出来的。

完整的数学形式则是德国的克劳修斯（Rudoff Julius Emanuel Clausius，1822—1888）在 1850 年首先提出的，他全面分析了热量 Q、功 W 和气体状态的某一特定函数 u 之间的联系，考虑一无限小过程，列出全微分方程：dQ = du + AdW，他写道：“气体在一个关于温度和体积所发生的变化中所取得的热量 Q，可以划分为两部分，其中之一为 u，它包括添加的自由热和做内功所耗去的热（如果有内功发生的话），u 的性质和总热量一样，是 V 和 t 的一个函数值，因而根据其间发生变化的气体初态和终态就已经完全确定；另一部分则包括做外功所消耗的热，它除了和那两个极限状态有关外，还依赖于中间变化的全过程。”

这里的 u 后来人们称作内能，A 是功热当量，W 是外功。克劳修斯虽然没有用到能量一词，但实际上已经为热力学奠定了基石。

W．汤姆孙（William Thomson，即开尔文勋爵，Lord Kelvin，1824—1907）在 1851 年更明确地把函数 u 称为物体所需要的机械能（mechanical energy），他把上式看成热功相当性的表示式，这样就全面阐明了能、功和热量之间的关系。

1852年，W．汤姆孙进一步用动态能和静态能来表示运动的能量和潜在的能量。1853 年兰金（W．J．M．Rankine，1820—1872）将其改为实际能和势能，他这样表述能量转化与守恒定律：“宇宙中所有能量，实际能和势能，它们的总和恒定不变。”

1867 年在 W．汤姆孙和泰特（Tait）的《自然哲学论文》中将上述实际能改为动能，一直沿用至今。

我们可以用一张联络图来表示能量转化与守恒定律的建立过程，如图 2 – 23。

[1] Magie W F．A Source Book in Physics．McGraw-Hill，1935．151

[2] 转引自：Γелькфер Я М．История и Методология Термодинамикии Статистическоǔ физики．Высшая Школа，1981．136

[3] 转引自：Elkana Y．The Discovery of the Conservation of Energy．Harvard，1974．119

[4] 同注 2

[5] 转引自：Holton and Roller．Foundations of Modern Physical Science．Addison-Wesley，1965．345

[6] 转引自：Lindsay R B．Energy：Historical Development of the Concept．Dowden：Hutchinson & Ross，1975．284

[7] 转引自：Lindsay，ed．Applications of Energy Nineteen Century．Dowden：Hutchinson & Ross，1976．7

[8] The Scientific Papers of J．P．Joule，Vol．1．Tayler，1884．149

[9] The Scientific Papers of J．P．Joule，Vol．2．Tayler，1884．328

发布时间：2010/9/2 下午12:27:37  阅读次数：14115