矩阵的基础知识

此篇文章来自于http://www.riemers.net/index.php，原文地址分别是http://www.riemers.net/eng/ExtraReading/matrices_geometrical.php，http://www.riemers.net/eng/ExtraReading/matrices_maths.php，http://www.riemers.net/eng/ExtraReading/homogenous_matrices.php。

矩阵和DirectX

在DirectX 程序中使用的矩阵究竟是什么？也许你已经了解了矩阵的概念，但还想完全控制它们；也许你不关心数学，但想了解矩阵的几何意义，如果属以上两种情况，那么这个教程就是为你准备的。

首先讨论矩阵的几何意义，它可以总结为3个容易理解的特性。第二部分涵盖矩阵使用的数学知识，最后讨论齐次矩阵，它是DirectX实际使用的矩阵。

变换（Transformations）

你应该已经知道变换（transformation），它将任意3D点的坐标变换到另一个3D点的坐标。下图你可以看到3个基本变换的例子：

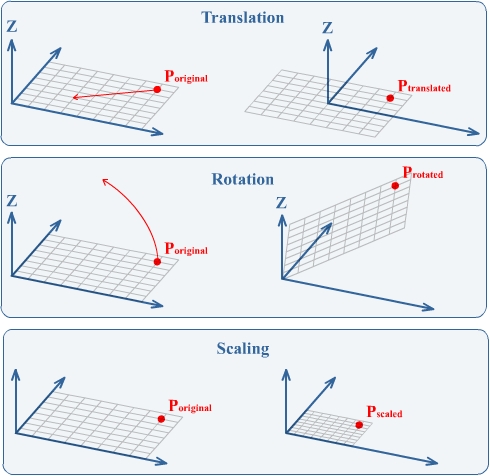
第一个变换只是简单地将3D空间中的所有点移动到左下方，这种变换叫做平移（translation）。第二个变换是旋转（rotation），所有点绕一个指定轴旋转，本例中是绕Z轴旋转。最后一个基本变换是缩放，所有点的坐标乘以一个特定的数值。

我将它们称为基本变换，是因为你能想象的任何变换都可以用这三个基本变换的组合表示。

下图你可以看到平移的结果，然后还要进行旋转：

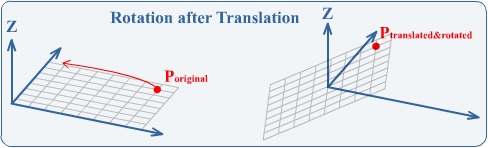
这实际上就是我们在系列1中使用的变换，我们首先将地形中点移动到初始位置，然后当用户按键时旋转它。

3个特性

特性1：矩阵可以看做一个特殊（但并不复杂）的元素，可以表示上述变换。所以假如你有3个矩阵：Mtrans, Mrot和Mscal，它们分别对应一种变换。

特性2: 如果你将一个矩阵乘以对应的3D点坐标，就可以获取变换后的点坐标，如下图所示：

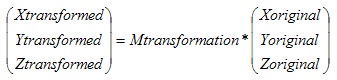
这意味着对任意点，你可以简单地通过将它的坐标乘以一个矩阵获取它的投影、旋转和缩放！

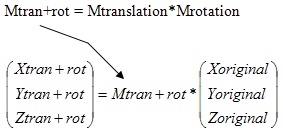
特性3: 如果你将两个矩阵M1和M2相乘，会获得一个新矩阵M3。对应这个新矩阵M3的变换即对应前两个矩阵的变换组合。第三个特性非常有用。例如上面平移后旋转的例子中，计算给定点的位置的一个方法是首先计算经过平移矩阵M1的变换，然后将结果乘以M2计算旋转，这让你必须为每个点计算2次，由下图表示：

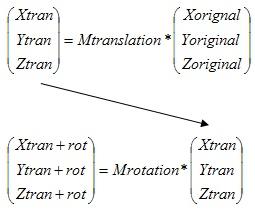
使用第三个特性，你只需简单地先计算M1和M2的乘积获取M3。然后将点乘以矩阵 M3获取点的平移并旋转后的坐标！2个矩阵的乘法很快(64次乘法和48次加法)，而变换场景中的所有点要慢得多(每个点16次乘法和12次加法)

矩阵数学

阅读这部分内容时意味着你已经对矩阵有了一个基本的认识，但你还想更深入了解。

所以首先学习一下矩阵看起来象什么。一个矩阵其实就是一个数据表格，就像Excel表格一样，或者也可以看成一个2维浮点数数组。要处理3D坐标，需要使用矩阵的3行和3列，如下图所示：

你可以将一个3D点的坐标作为一个矩阵的一列和3行，点和矩阵间的乘法如下定义：

现在你应该知道了所有知识。如你所见，并不是很难。下面举一个例子。设3D空间有一个坐标为(6,18,9.5)的点。先看一个简单的例子：我们想将场景变大为2倍，这意味着我们要缩放2倍，一个简单的缩放矩阵如下所示：

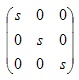
结果是：

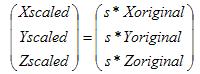
在这个例子中，s = 2，所以点的坐标变为(12, 36, 19)。

下面看一下旋转矩阵，它看起来有点复杂，但记住所有sin和cos实际上就是一个介于-1和+1之间的数值。下面三个矩阵表示绕X,Y和Z轴的旋转，θ为旋转角度：

例如将点(10,5,0)绕Z轴旋转45度，我们的旋转矩阵如下：

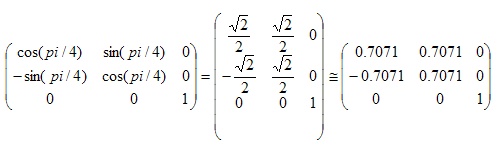
因为pi=3.14对应180度，45度对应pi/4。结果是：

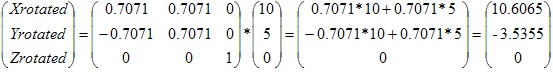
所以当我们将点(10,5,0)旋转45度，结果是点(10.6065, -3.5355, 0)！幸运的是，DirectX可以为你完成这些运算，但现在我们理解了工作原理。

现在还有一个问题，你无法通过乘以一个点的坐标获取点的平移信息。要解决这个问题，DirectX使用了齐次矩阵（homogeneous matrices）。

齐次矩阵

如果你使用DirectX访问一个矩阵，你会看到16个数据项，这意味着4行和4列。选择这种方式是为了让矩阵也可以表示平移。

要平移一个点，我们需要添加一个数字。使用3x3矩阵，我们只能获取初始矩阵的倍数。所以在X,Y和Z边上需要添加一个常数。为了简单起见，设为1。从现在开始，我们使用4个坐标表示一个3D点。例如，位于(10,5,0)的点的坐标为(10,5,0,1)。这些坐标称为点的齐次坐标（homogeneous coordinates）。

缩放和旋转矩阵保持不变，但多了一个额外的行和列其值为0，但m44值为1。下图你可以看到以齐次形式的缩放和Y旋转矩阵：

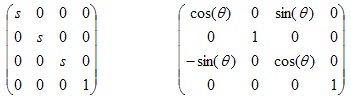
看起来有点复杂，但现在我们可以定义一个平移矩阵了：

让我们看一个小例子。如果我们想将点(10,5,0)移动(-8,2,4)。可以这样做：

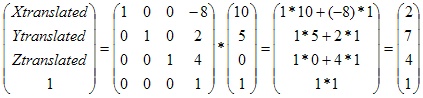
结果是(2,7,4)。但这里我仍想强调3个基本特性：

1) 我们有一个矩阵对应每个基本变换

2) 将点的坐标乘以一个矩阵会获得变换后的坐标

3) 两个矩阵相乘获得一个新矩阵，对应变换的组合

如果你理解以上特性，你会注意到第4个坐标没有几何意义，它只是让我们可以定义一个平移矩阵。

你会注意到有时这个常量不是1。事实上，通用规则是只需简单地将X,Y和 Z 坐标除以第4个坐标，我们将第4个坐标称之为W坐标。

简单地说：(20,10,0,2) = (10,5,0,1)，这两个坐标表示的是同一个3D点(10,5,0)，所以从4个坐标中获取3D点的简单规则是：

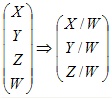
发布时间：2010/5/6 下午4:26:42  阅读次数：13451