万有引力与潮汐

岳阳市第四中学 缪纯丽 选自《物理教师》2009年第12期

高中一年级学过万有引力后，有学生问：“我们地理课中讲到海水的潮汐是由于万有引力引起的，请老师跟我们解释一下。”对于这一问题，还得从天体的运动和万有引力来分析。

1什么叫做潮汐？

潮汐是指海洋中的水按一定规律的涨落现象，白天海水的涨落称为“潮”，晚上海水的涨落称为“汐”。潮汐主要是由于月亮和太阳对于海水的引力造成的。但由于月亮距离地球较近，它绕着地球运动，海洋潮汐主要是月亮的影响为主，太阳的影响相对小一些。

海洋的潮汐跟航海业、海洋渔业和国防有着密切的关系；海洋的潮汐可以产生巨大的能量，世界各国已经利用或正在利用潮汐发电。因此，研究和利用潮汐规律有着非常重要的意义。

2引潮力的产生

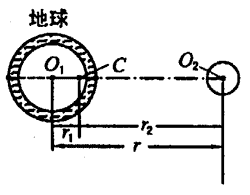我们主要分析月亮的引力而产生的引潮力，为了分析问题简单起见，假设地球表面全部被海水包围，且月亮和地球都是均匀球体。质心都与其球心重合。月亮绕地球转动，可以看作两球绕其公共质心C作圆周运动，如图1所示。公共质心C的位置可这样确定：设地球的质量为M，月亮的质量为m，两球心相距O₁O₂＝r，两球心相距公共质心O₁C＝r₁，O₂C＝r₂，则有

Mr₁＝mr₂，r₁＋r₂＝r。

因此得到

r₁＝mr/(M＋m)，r₂＝Mr/(M＋m)。

如果设地球的半径为R，又由r＝60R，M＝81m，代入上式得到，r₁＝3R/4 ，即公共质心c在地球内部，距离地心为3R/4 处。

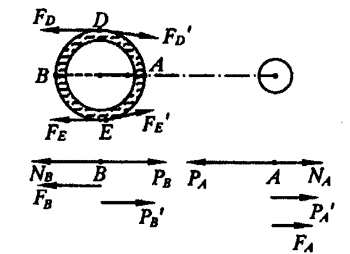
如果研究海水中向着月面的A质点和背着月面的B质点，如图2所示。设地球对两质点的引力分别为PA和PB，月亮对它们的引力分别为P_A′和P_B′，海水的支持力分别为N_A和N_B，绕公共质心转动的惯性离心力分别为F_A和F_B，在转动平衡时，有

N_A＋P_A′＋F_A=P_A，

N_B＋F_B＝P_B＋P_B′。

将上面两式整理得

N_A＝P_A－（F_A＋P_A′），

N_B＝P_B－（F_B－P_B′）。

其中（F_A＋P_A′）和（F_B－P_B′）是惯性离心力与月亮引力的合力。

若此合力为零，则不会出现潮汐现象，海水的涨落就是由这个合力造成的。因此，这个合力被称为引潮力。显然，A质点所受的引潮力方向是指向月亮而背离地球的。对于B质点所受的引潮力方向，我们作以下分析：设地球和月亮绕公共质心C转动的角速度为ω，A和B的转动半径为r_AC和r_BC，取质点A和质点B具有相等的质量Δm，则有

F_A＝Δmr_ACω²和F_B＝Δmr_BCω²。

由前面的计算可知r_AC＝3R/4 ，rBC＝7R/4 ，得到F_A＜F_B。另一方面，可以认为地球各个质元Δm所受到的惯性离心力的合力等于月亮对地球的引力，即

F_合＝GmM/r² ＝GmΣΔm/r² 。

式中G为万有引力常数，地球的各个质元Δm所受的惯性离心力平均值为

f＝GmΔmr/² 。

对上面几个力比较，我们得到

F_A＜f和F_B＞f＞P_B′。

则质点B所受的引潮力方向也是背离地球的。可见，无论是面向月亮还是背向月亮的海水，都要受到背离地球的引潮力的作用而形成海水高峰。A点的海水高峰叫顺潮，B点的海水高峰叫对潮。

我们如果对图2中的D、E两点进行分析，可以得到其引潮力是指向地球内部的，则D、E两处的海水会形成低谷。

同理，如果对于地球和太阳进行分析，它们绕其公共质心转动，相应的惯性离心力与太阳引力的合力，就构成太阳的引潮力。虽然太阳的质量比月亮大，但太阳离地球的距离远远大于月亮离地球的距离，所以太阳的引潮力要比月亮的引潮力小很多，潮汐现象主要是由于月亮的引潮力起着决定性作用。

3潮汐现象的规律

由于地球的自转。地球上的各个点要依次经过图2中的A、B、D、E的位置。这就是同一地点的海水，每天要涨落两次的原因。潮汐又有大潮和小潮、近地潮和远地潮、近日潮和远日潮，都是由于引潮力的变化而产生的。

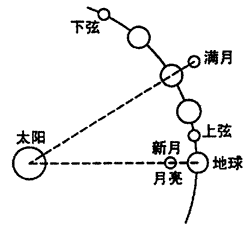
大潮和小潮是由于太阳引潮力的影响而形成的。当太阳、地球和月亮运动到同一直线时，如图3所示，太阳和月亮的引潮力叠加，海水所受到的引潮力最大，以致海水高峰最大，称为大潮。大潮总是出现在农历的初一（新月）和十五（满月）左右。当农历的初七、初八（上弦）和廿三、廿四（下弦）时，太阳、地球和月亮的相对位置几乎构成一个三角形。这时月亮的引潮力被太阳的引潮力抵消了一部分。海水所受到的引潮力最小，因而形成的海水峰最小，称为小潮。

每次潮汐的大小，还与月亮或地球在其轨道上的位置有关。实际上月亮绕地球运动的轨道是椭圆，地球位于此椭圆的一个焦点上。因而在月亮运行的过程中，当月亮位于近地点时引潮力最大，称为近地潮；当月亮位于远地点时引潮力最小，称为远地潮。同样，地球绕太阳运动的轨道，也有近日点和远日点。与此相应，亦有近日潮和远日潮。近日潮在一月初，远日潮在七月初。

发布时间：2010/4/7 下午1:00:46  阅读次数：13238