泊松

上海市徐汇业余大学 曾铁 选自《物理教师》2009年第7期

1．简历

法国力学家、物理学家和数学家S.D.泊松（1781～1840）出生于法国卢瓦雷省的皮蒂维耶，故于巴黎郊外的索镇。

泊松曾在枫丹白露中学学习，遵从父亲（其父是退伍军人，当过村长等）之命，先读医科。青年时代，他研究过一种如何分啤酒的数学游戏。

1798年，他以第1名的成绩进入著名的巴黎综合工业学院（法国研究型大学，位列法国四大名校之首；又译为巴黎多科工艺学院）改学数学，他的数学才能很快受到了老师、著名数学家P.S.拉普拉斯（1749～1827）和J.L.拉格朗日（1736～1813）等的赏识。

18岁时，泊松发表关于有限差分方程的积分论文，初露锋芒。1800年，他又在巴黎综合工业学院发表了2篇数学论文，受到法国数学家A.M.勒朗德（1752～1833）的好评。

1800年，他毕业留校任教。因其优秀的研究论文，被指定为讲师；1802年任副教授；1806年接替法国物理学家、数学家J.B.J.傅立叶（1768～1830）任教授。

法国物理学家N.L.S.卡诺（1796～1832）、A.J.菲涅尔（1788～1827）、著名数学家A.L.柯西（1789～1857）和德国数学家P•狄利克雷等是泊松的学生。泊松和拉普拉斯、拉格朗日关系很好，既是师生、又是朋友，甚至有父子之情，这两位恩师对泊松的研究、进步帮助较大。

1803年，S.D.泊松加入法国科学普及协会。1804年，他推荐法国物理学家D.F.J.阿拉果（1786～1853）担任巴黎天文台秘书。1808年，泊松任法国经度局天文学家；1815年。任圣希尔军事学院检查员；1827年，继拉普拉斯之后任法国经度局几何学家。1809年，巴黎理工学院成立，他任该校的数学和力学教授。

1812年，因法国物理学家E.L.马吕斯（1775～1812）去世出现空缺，泊松当选为法国科学院物理学部院士。但是，泊松一直反对J.B.J.傅立叶在法国科学院任职。

1816年，泊松任索邦大学（巴黎大学）教授，并任巴黎综合工业学院毕业生主考官；1820年，任大学皇家教育顾问，1826年，被选为彼得堡科学院名誉院士；1837年，又被封为男爵。

1817年，泊松和N.巴尔迪结婚。泊松是一个无神论。

1829年夏天，泊松在巴黎与来访的德国数学家C.G.J.雅可比（1804～1851）进行学术交流。

1837年，作为法国科学界的代表，他成为贵族院的议员。

S.D.泊松是19世纪伟大的力学家、物理学家和数学家；他既是优秀的科学家，也是优秀的教师。泊松曾说：“人生只有两样美好的事情，发现数学和教数学。”他精力充沛，研究领域广泛，主要研究领域是数学物理，撰写了一些关于力学、热学理论的论文。在数学史上，泊松在所有领域中是一个称职的他人工作的扩展者。

他一生致力于理论研究，其成果为理论物理及数学物理奠定了基础。泊松将数学理论应用于物理问题的研究，对近代理论物理的发展起到了指导作用。导体表面电荷的分布、导体附近的电力与电位、导体与绝缘体各种组合的电容量等问题，泊松证明都可以用数学方法予以解决；他的许多研究成果都涉及到现代科学的基础理论。泊松始终从事数学和物理学的研究与教学，其主要工作是将数学应用于力学和物理学之中，对数学和物理学均作出了重要贡献。他的科研范围很广，研究过理论力学、电磁学、外弹道学、水力学、固体导热问题和固体与液体运动方程、毛细现象等；他对势论、积分理论、傅立叶级数、概率论和变分方程、流体动力学作过详尽的探究；在定积分、有限差分理论、微分方程、积分方程、行星运动理论、弹性力学和数学物理方程等方面均有建树。因此，数学和物理学中有许多用他的名字命名的名词和专用术语，例如，泊松括号、泊松比、泊松方程、泊松积分（公式）、泊松常数、泊松分布、泊松定律、泊松级数、泊松变换（位势变换）、泊松回归、泊松代数、泊松二项试验模型、泊松流、泊松核、泊松效应、泊松变量、泊松求和公式、泊松大数定理、泊松稳定性、泊松过程（两种随机过程之一）、泊松密度函数和泊松正向稳定轨线，等等。

他一生发表研究论文300多篇，出版了多部重要、影响力较大的专著，如《力学教程》、《热学的数学理论》、《分析教程》、《关于刑事案件和民事案件审判概率的研究》和《毛细管作用新论》等等。

2．主要科研工作

S.D.泊松的科学生涯始于研究微分方程及其在摆的运动和声学理论中的应用，他的工作特点是应用数学研究各类力学和物理问题，并由此得到数学上的新发现。泊松没有作出过贡献的数学分支极少，他的电磁理论的研究，实质上是创建了数学物理的一个分支。

他是19世纪著名分析学家之一，也是一流的数学物理学家。泊松研究分析学的主要目的，是利用分析学说明、解释自然，并主要应用于力学与物理学。他为建立完整的分析力学体系做出了贡献，也是弹性的数学理论的奠基人之一。

在天体力学方面，他研究过太阳系诸行星的轨道，尤其是地球轨道有无长期摄动的问题，以及月球和其他大行星运动理论；泊松推广了拉格朗日、拉普拉斯有关月球和行星轨道稳定性的研究，计算出了球体和椭球体之间的引力等；他讨论行星稳定性问题时，提出可将拉普拉斯已解决的一阶近似在扰动力作用下的情况，扩展至二阶近似。他的太阳系稳定性研究与引力论研究发展了拉格朗日、拉普拉斯的思想；泊松用行星内部质量分布表示重力的公式，对20世纪60年代后通过人造卫星轨道确定地球形状的计算仍有实用价值；他还建立了星系动力学的一个基本方程，即泊松方程。

泊松对发散级数作过深入的研究，奠定了发散级数求和的理论基础，并引进了可和性概念。把任意函数表示为三角函数和球函数时，他广泛地使用了发散级数，并用它求解微分方程：他还将许多含有参数的积分化为含参数的幂级数，并将摄动函数展开成幂级数和三角级数的混合级数（泊松级数）。他的关于定积分的一系列论文以及在傅立叶级数方面取得的成果，为后来的数学家P.G.L.狄利克雷和黎曼的研究铺平了道路。

泊松等人是在万有引力定律基础上发展、完善起来的。数学形式简单、优美且实用的势论，构造了万有引力和静电作用的超距作用理论。他的势论研究成功之处，在于他将所考虑的问题集中在所求点及其附近，而非象拉格朗日、拉普拉斯那样只将注意力放在产生势的外部系统上。他指出，由于万有引力定律和库仑定律都遵从平方反比关系，所以关于万有引力的数学分析方法可以用来分析静电现象。他认为在静电学中可以找出与万有引力情况相似的势函数V来，并能通过它研究静电学的问题。

他是最先提出把万有引力势理论移用到静电学和静磁学中的人之一，并发展了静电学的解析理论。当时的业内专家对泊松的静电学理论及其成就评价道：他“驱散了至今还笼罩着物理学许多领域的阴霾”。

泊松的静电学理论及其成就，还在英国的科学界颇有影响。为此，英国物理学界开始重新认识电学，并确立了电学的重要地位。英国著名数学家G.格林（1793～1841）的研究深受泊松影响，格林的工作为培育、形成数学物理中著名的剑桥学派（著名物理学家W。汤姆生、L.瑞利和J.C.麦克斯韦等都是该学派的成员）做出了巨大贡献。

泊松在热力学发展中也起了重要作用，他指出热学研究应当数量化、精确化，热力学问题要用数学方法处理。泊松的经典著作《热学的数学理论》等书，对德国物理学家G.S.欧姆（1787～1854）的电学研究等也发挥了积极的作用。

他对用初等函数及其积分表示偏微分方程的解作过研究。他认为所有偏微分方程均可用级数展开式来求解，这些级数的每一项都是一些函数的乘积，其中每个函数又是一个独立变量的函数，这类展开式包括了最一般的解。泊松曾说，拉格朗日提出过任意函数可表示为傅立叶级数，时间比J.B.J.傅立叶早。

泊松还给出了调和分析中的泊松求和公式，欧拉一马克劳林求和公式的余项也是泊松加上去的。

泊松也是19世纪概率、统计领域的领军人物之一，他改进了概率论的运用方法，尤其是用于统计的方法，导出了在概率论和数理方程里有重要应用的泊松积分。泊松主张概率方法具有普适性，并与当时持反对观点的学者进行辩论。泊松从事概率论研究，与他通过力学、物理学问题研究数学的做法不同，泊松则是根据法庭审判问题研究概率、统计的。将概率和统计理论运用于社会科学的研究之中，泊松是先行者之一。

1809年，泊松为研究行星运动创立了一种有用的数学分析工具，即微分方程的运算符号“泊松括号”（一种偏微分方程的缩写数学符号，具有一些特殊的性质），它能用简单的形式将经典力学的基本方程表示出来。同年，泊松研究太阳系稳定性问题时，提出了新的、更广泛的稳定性定义。这一年，他在巴黎综合技术学校学报发表了论文《关于行星平均运动的久期不均等》和《关于力学问题中任意常数的变化》。

1811年，泊松在《论导体表面电荷的分布》一文中，根据拉普拉斯等人的均匀椭球球面的引力定律，解决了C.A.库仑（1736～1806）没有解决的电荷面密度与导体形状的关系问题，其结论是均匀椭球面上的电荷密度与通过这一点的法线到对面距离的长度成正比。推而言之，即导体表面曲率越大，电荷面密度越大。同年，他又把最先是为万有引力而发展起来的势论，转用到库仑定律和静电学之中，建立了计算电势的方程。同年，他写作了《力学教程》。

1812年，泊松提出宏观电荷中性是物质的自然状态之概念，充电可作为两种电荷分离的一种手段，还指出势函数在电学里有着重要的用途。同年，他发现拉普拉斯微分方程ΔV＝0只在固体之外才是正确的。

1811～1812年，泊松发表了2篇关于静电学势论的论文。1813年他用数学方法证明处于静电平衡的导体内部任何带电粒子所受的力为零，否则，导体内部就会有电荷流动。泊松还解决了当时的电学难题，即电荷在相互临近的诸导体表面上的分布问题，其基本原理和思路是每个导体的内部各处，静电合力必须为零。他认为，电荷自由分布在任何导体表面时。势函数V在导体表面上的数值必定是一常数。

1813年，泊松发展了拉普拉斯方程，他撰文指出，如观察点在充满引力物质的区域内部，则拉普拉斯方程（1777年，拉普拉斯提出一个质量系统对空间任意点的引力，可用一个函数对空间这一点的坐标的微商来表示，此函数叫做拉普拉斯函数，用V记之，它等于质量系统中各质量除以到所求点的距离再求和。1782年，拉普拉斯证明拉氏函数V满足拉普拉斯方程，即ΔV＝0。这是一种二阶偏微分方程）应改为ΔV＝－4πρ，这就是著名的泊松方程（ρ为引力物质的密度或电荷密度）。他强调要重视势函数V在电学理论中的应用，并提出导体表面是等势面。

泊松方程是一个常出现在数学物理各领域的重要方程，它完善了拉普拉斯方程，广泛用于电学、磁学、力学、热学等各种势场的研究与计算之中。当空间充满各向同性、线性和均匀的媒质时，静电学的泊松方程为ΔV＝－ρ/ε_rε₀ （ρ为自由电荷密度，ε_r、ε₀分别是媒质的相对介电常数和真空介电常数）；静磁学的泊松方程（矢量方程）是ΔA＝－μ₀μ_rJ（A为磁矢势，μ₀、μ_r分别是媒质的相对磁导率和真空磁导率，J是传导电流密度）。

1811年，泊松出版了理论力学名著《力学教程》（第1、第2卷），1833年又增补出了第2版。他首先用冲量分量形式研究、撰写分析力学，《力学教程》在很长时间内是标准的大学教科书。

1812年起，泊松长期研究弹性力学里的平板问题，得到了圆板弯曲和振动问题的解答。他讨论过杆件的纵向、横向和扭转等振动问题，还首先得出了弹性球体径向自由振动的解答，最先用三角级数研究梁挠度曲线问题，第1次得到了板的挠曲方程等。

1813年，泊松研究一类刚体定点转动问题（刚体只受重力作用，重心在OZ轴上，刚体关于O点的惯性椭球是旋转椭球），获得了轴对称重刚体定点转动微分方程的积分，并得到了精确解。

1809～1819年，泊松研究波动方程及其初值问题，得到了关于波的传播公式等。

1815年起，泊松开始研究热传导问题。分析热传导问题时，他使用了按三角函数、拉普拉斯曲面调和函数和勒朗德多项式等的展开式。1807年，J.B.J.傅立叶写出了热传导理论（1815年出版），它所依赖的基本思想是把温度分布分解成空间正弦分量。泊松等人对此表示怀疑，并提出了批评。泊松的热学研究均收录在其代表作《热学的数学理论》之中。1835年，这部专著出版；1837年又增补再版。书中主要讨论了二维稳定热传导等问题，泊松绝热方程便在该书里。

1815年，他注意到并在1820年的一篇论文中，讨论了沿复平面路经所取的复函数的积分之用处；泊松是第1个沿复平面上的路径求复变函数积分的人。

1816年，他发表研究水波的专著《关于波的理论报告》。1817年，泊松在其出版物中对序列收敛的条件提出过正确的概念，并提出了一般振动及波动理论。

1817年3月，法国科学院为鼓励对光衍射问题的研究，提出了2个征文题目，作为1819年数理科学的悬奖项目，即（1）利用精确的实验确定光的衍射效应；（2）依据实验用数学归纳法推求光线通过物体附近时的运动情况。1818年4月，法国物理学家A.J.菲涅尔（后被称为“物理光学的缔造者”）提交了应征论文，他从横波观点出发，圆满地解释了光的偏振；用半波带法定量地计算了圆孔、圆板等障碍物产生的衍射花纹，而且与实验符合得很好。该文还用数学方法将惠更斯原理发展为后来的惠更斯—菲涅耳原理，它进一步考虑了各个次波叠加时的相位关系。但是，菲涅尔光的波动理论遭到了光的粒子说者的反对。征文竞赛5人（拉普拉斯、J.B.毕奥、阿拉果、盖•吕萨克和泊松）评奖委员会中光的粒子说支持者S.D.泊松，运用菲涅尔征文里的波动方程推导出一个关于圆盘衍射的结论，即如果菲涅尔的波动方程是正确的，那么当把圆盘放在光束中，就会在圆盘后面一定距离处屏幕上盘影的中心点出现一个亮斑。泊松认为这是荒谬的，并宣布已经驳倒了光的波动理论。阿拉果、菲涅耳等人先后检验泊松的预言，实验却都证实了泊松的结论，即盘影的中心点确实出现了一个亮斑。所以，征文获奖者是菲涅尔。如此，这个亮斑就被称为“泊松亮斑”。自19世纪初开始，光的波动理论被更多的人认可和接受。直至19世纪末光的波动说取得绝对的优势，“泊松亮斑”的由来与影响起到了重要作用。“泊松亮斑”也是光学史乃至物理学史、科学史中一个重要而有趣的事件与故事。

1820年9月，泊松和法国物理学家A.M.安培（1775～1836）一起利用实验研究丹麦物理学家H.C.奥斯特（1777～1851）的电流磁效应理论问题。

1821年，泊松运用波斯考维奇的原子论观点，把平板弯曲视为由质点系组成的理想薄膜，在用分析力学推导的基础上，依据质点之间作用力与距离改变成正比，推出了各向同性弹性体的微分形式的平衡方程。这一年，泊松研究球形磁体问题时，在推导磁体产生的势过程中发现了面积分与体积分的关系，这可以说是数学分析中格林定理的先声。同年，他在《时间的知识》杂志发表论文《关于月球的天平动》。同年，在泊松等人的支持、鼓励下，19世纪伟大的法国数学家A.L.柯西出版了几部微分学和数学发展史中的重要著作，即《分析教程》、《无穷小计算讲义》和《无穷小计算在几何中的应用》。

泊松将磁视为两种不同性质的磁流体，从而建立了泊松静磁学理论。1821～1822年，他发表了两篇静磁学论文；它们又分别于1824年摘要刊载在法国的《化学和物理学年鉴》（第25卷）和英国《科学季刊》（第17卷）上。1823年，他又发表了一篇磁学论文。在C.A.库仑研究的基础上，泊松提出了磁体间相互作用的势函数积分方程，把磁的研究发展到了定量阶段。

1823年，泊松研究理想气体的绝热压缩与绝热膨胀问题，他从理论上探讨了绝热过程中气体压强与体积的变化规律，此规律由拉普拉斯写成公式：ρV^γ＝C，即热学里的泊松定律（分析力学中有一个定律也叫泊松定理，它是解正则方程的一个重要方法）。其中γ＝C_p/C_V ，它叫做比热容比，又叫泊松系数；C_p、C_V分别是定压比热和定容比热；C是常数。同年，他发表了用热质理论研究气体性质的相关论文。

1826年，泊松研究一个带电体表面的电势问题时，又将泊松方程具体、细化成3种形式，即ΔV＝0（导体表面无电荷）；ΔV＝－2πρ（电荷只分布在导体表面）；ΔV＝－4πρ（电荷分布在导体内部）。至此，泊松建立了完整的静电学势理论（Δ是拉普拉斯算符的简写）。

1827年，他在法国《科学院备忘录》上发表论文《关于地球绕其重心的运动》。 1828年，泊松发现：如果发光以太是一种类固体，那么光的横向振动必然伴随着纵向振动，这与当时光的波动说相矛盾。

由牛顿声速公式v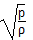＝ 算出的声速数值总比实验数据小，S.D.泊松等人分析后指出，声波中气体压缩和稀疏改变得很快，这不是等温过程，而应是绝热过程，所以牛顿声速公式要修改。修正的牛顿声速公式为v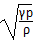＝（p是大气压，ρ是空气密度），其中γ＝1.41，它是空气的定压比热和定容比热的比值；由新声速公式得到的数值和实验数据吻合了。

1829年，泊松在《弹性体平衡和运动研究报告》中，用分子间相互作用的理论导出了弹性体的运动方程，发现弹性介质可以传播纵波和横波，并从理论上推出各向同性弹性杆在受到纵向拉伸时，横向收缩应变与纵向伸长应变之比是一个常数，这就是材料的“泊松比”之由来。“泊松比”又称横向变形系数（弹性体在侧向不受约束的情况下，纵向伸长时横向要同时收缩，此时横向张应变与纵向张应变之比的绝对值）。泊松推出的泊松比为0.25，但这个数值随材料而异，一般与泊松的理论值有出入。同年，他还推出了粘性流体运动偏微分方程，并给出了通解。这一年，泊松发表论文《关于类球体的引力》。1830年左右，在研究弹性介质中波的传播问题时，他论证了远离震源处纵波和横波的存在，即地震学里的P波（压缩波）与S波（剪切波）。同年，他将当时的法国物理学及其思想归为两类：物理力学和解析力学。他认为，前者“唯一的原理是把一切还原为分子运动，而这些分子是把力的效果从一点传到另一点并保持这些力之平衡作用的核心”，前者期望用牛顿平方反比定律这一数学格式，精密地描述宇宙的一切现象，这是牛顿范式；后者则强调现象的解析格式，轻视对物理原因进行讨论，这是非牛顿范式。

1831年1月，在泊松的提议下，年轻的法国数学家E.伽罗瓦（1811～1832）写了一篇数学论文，即《关于用根式解方程的可解性条件》（即“伽罗瓦理论”）送交法国科学院。泊松审读后却退回了这篇论文，理由是“难以理解”，并要伽罗瓦再写一份详尽的阐述。泊松未能赏识E.伽罗瓦，并发现、帮助这个数学天才是数学史上的一件憾事。同年，泊松发表《弹性固体和流体的平衡与运动一般方程研究》，首次完整地给出了说明粘性流体物理性质的微分方程，即本构方程；导出了流体力学中的纳维一斯托克斯方程，解决了无旋的空间绕体流动的问题，并推动了小振幅波理论的发展。这一年，他出版了《毛细管作用新论》。

1835年，他发表《关于均匀椭球体的引力》一文，精确计算出了由球体和椭球体引起的引力等。在概率与统计的研究中，他继承、发展了拉普拉斯概率理论，拉普拉斯概率研究路线图是其研究方向。为确定一个陪审员在裁定罪行上可能出错的概率，他考察、研究了许多有关著作、法律条文和法庭记录等。他的相关成果曾在法国科学院宣读。1827年和1832年，泊松在《天文年历》杂志发表两篇关于观察的平均结果概率的论文，它们评论了拉普拉斯名著《分析概率论》第4章。这两篇论文是《分析概率论》第4章的一个很好的导言，它们让拉普拉斯的误差理论通俗易懂和简单化了。1832年，泊松还发表了著作《关于判决概率的研究》。同年，就概率理论在法律领域的应用问题等，泊松与一批法国数学家发生了论战。1837年，泊松概率论的代表性著作《关于刑事案件和民事案件审判概率的研究》出版。“大数定律”这一名称就是泊松在该书引进的，他发展了“大数定律”。这本著作记录了他发现的“泊松分布”（二项式分布的一种特殊情况；当一给定试验中的成功概率是用试验的次数去除某一常数时，二项式分布就成了泊松分布），自然科学和社会科学中许多随机现象都遵从这种重要的概率分布，工业、农业、商业、交通运输、公用事业、医学和军事等领域常用到它。“泊松分布”曲线是一钟形状的曲线。泊松说过，“我建立了描述随机现象的一种概率分布”。在大量生产中当废品比例预计很小时，泊松分布对于产品检验和质量控制特别有用。

他也探究过常微分方程中贝塞尔方程的特殊情形；研究了积分方程问题；用变分法解决了许多弹性理论问题；还研究过膜的振动问题以及地球转动对弹道曲线的影响等。

泊松一生都对摆的研究感兴趣，直到晚年他仍在用许多时间和精力从事摆的研究。

3．其他

泊松是19世纪法国分析学派的代表性人物，法国数学家柯西在其名著《分析教程》的序言里说：“在综合工业学院，许多人非常好意地引导我迈进了科学生涯的第1步，在他们之中，我特别感谢地提到拉普拉斯和泊松，他们非常关心这部分析教程的出版，所以我才写出这部教程。”

泊松在拉普拉斯葬礼上发表颂词，称赞拉普拉斯是一代天才和圣贤，是“法国的牛顿”。泊松说拉普拉斯是一位急于开拓新领域的自然科学家，尤其善于解决难题；“对科学的热爱即是他的生命，至死方休。爱的冲动源于内心火热，不拜他人所赐，与他结交的人更是对他恭敬从命，并称赞有加。——他的观点使我的思想焕然一新”。泊松还这样评价拉普拉斯：“数学的分析在他看来是有着最广泛的应用的一个工具，他经常通过使特殊的方法以满足特殊问题的需要。”拉普拉斯“是通过把最高贵的数学引进来以服务于理解自然的科学家”。

参考文献：

1．全日制普通高中教科书（必修加选修）《物理（第3册）》。北京：人民教育出版社，2003。29

2．宋德生等。电磁学发展史。南宁：广西人民出版社，1989。103～113

3．M•克莱因。古今数学思想（第3册，第4册）。上海：上海科技出版杜，1980。

4．http://zh.wikipedia.org/zh-cn，“泊松”。

5．王幼军。拉普拉斯概率理论的历史研究。上海：上海交通大学出版社，2007。

6．王竹溪。中国大百科全书（物理卷）。北京：中国大百科全书出版社，1987。

7．李文林。数学的进化。北京：科学出版社，2006。

发布时间：2010/3/24 上午11:06:10  阅读次数：16437