线速度方向变化快慢用什么物理量描述？

上海市杨浦区教师进修学院 李沐东 选自《物理教师》2009年第7期

在进行高中物理“匀速圆周运动”章节的学习时，常会在各类教科书和参考资料上看到这样的提法：“向心加速度是描述线速度方向变化快慢的物理量”。例如“向心加速度的方向始终与速度的方向垂直，它只是描述物体运动速度方向变化的快慢程度，并不描述运动速度大小的变化快慢程度。”；“向心加速度表示做匀速圆周运动的质点速度方向变化的快慢。”。

产生上述提法的根源在于：做曲线运动的物体不仅速度的大小可以发生变化而且线速度的方向时刻在变化，因此物体具有加速度，且加速度与速度成一定夹角。这种情况比较复杂，但我们由匀加速直线运动和匀速率圆周运动这两个特殊情况的加速度特点可以得到一些启示，即可以把一般的加速度a分解为两部分：一个分量方向与速度方向在同一直线上，称为切向加速度a_τ；另一个分量方向与速度方向垂直，称为法向加速度a_n。再从加速度是描述速度变化快慢的物理量这一概念出发，从而说：切向加速度是描述速度大小变化快慢的物理量，而法向加速度(对于圆周运动即为向心加速度)是描述速度方向变化快慢的物理量。这一说法似乎顺理，但成章吗？

这一观点在解释质点做匀速圆周运动时问题不大，但在解释做绕轴转动的刚体时，就会遇到难以调和的矛盾。如下例。

一根轻质细杆绕其一端O点匀速转动，杆上分布A、B两点，如图1所示。已知r_A＜r_B，当轻质杆从位置1转到位置2时，A、B两点的线速度方向改变的角度一致，所以线速度的方向改变快慢一致；但由于有a_n＝rω²，所以两点的向心加速度有a_A＜a_B的关系，这说明向心加速度并不是描述线速度方向变化快慢的物理量。

由此，一部分物理教师对上述说法提出异议，因A、B两点的角速度ω是相同的，从而提出“角速度ω是标志圆周运动的线速度的方向变化快慢的物理量”的观点。

这两个观点孰对孰错。杂志上也有不少相关的讨论文章，各持己见。那么线速度方向变化快慢到底该用什么物理量来衡量？本文拟从定义速度方向变化快慢的物理量出发，对相关物理量的物理意义和数学定义式进行分析，以澄清认识。

首先对一般曲线运动的速度方向变化的快慢研究入手，对于速度方向变化快慢可以作如下推导：

d（v/v）/dt＝(vdv/dt－vdv/dt)/v²＝va/v²－va_τ/v²＝a/v－va_τ/v²＝(a_τ＋a_n)/v－a_τ/v＝a_n/v

这里（v/v）为速度方向的单位矢量，其大小为1，只表示速度的方向，因而d（v/v）/dt即表示速度方向变化的快慢。

根据上述的推导，描述速度方向变化快慢的物理量应为a_n/v，即法向加速度除以速率，方向为法向加速度的方向，单位为s^-1。

对于匀速圆周运动，a_n为向心加速度，v为线速度的大小。由于v值不变，所以对于单个质点的匀速圆周运动，a_n/v为一定值，用a_n相替代，似乎不会出现矛盾，所以导致有人认为：“向心加速度是描述线速度方向变化快慢的物理量”。但a_n/v与a_n数值上一般不同、单位也不同，所以“向心加速度是描述线速度方向变化快慢的物理量”的说法不妥。

对于匀速圆周运动有a_n＝vω，所以上式比值的大小为ω。无论是单个质点匀速圆周运动还是刚体绕轴匀速转动，ω均不变，所以导致有人认为：“角速度ω是描述线速度方向变化快慢的物理量”。虽然a_n/v与ω的大小相同、单位相同，但方向不同，两者的物理意义也不同，所以“角速度ω是描述线速度方向变化快慢的物理量”的说法也不妥。

根据上述的分析可知，a_n/v是描述速度方向变化快慢的物理量，当然也适合描述圆周运动线速度方向变化的快慢。线速度方向变化的快慢均不能以a_n与ω来描述。鉴于高中阶段学生的理解力与知识储备，不便于讨论线速度方向变化快慢的问题，高中阶段最好回避这个问题。

既然向心加速度a_n不是描述线速度方向变化快慢的物理量，那它的物理意义到底是什么呢？

正如本文开始所述，一般曲线运动的加速度求解较难，所以将其分解为切向和法向两个分量，再进行求解。在实际求解一般曲线运动的加速度时，还把曲线的每个元段看成是所在圆周的一部分的思想，即以圆周运动的加速度推导来求解曲线运动的加速度。以下就通过圆周运动的加速度的推导，来揭示向心加速度的物理意义。

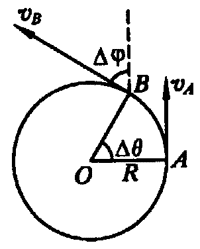在圆周运动中，线速度的方向时刻发生变化，如图2所示。取质点在某一点A的线速度v_A，当质点运动到B点时线速度为v_B。将线速度v_A、v_B进行平移，构成图3所示的矢量几何图。

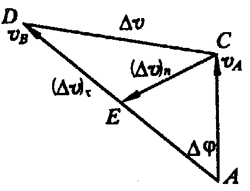
在矢量v_B（即线段AD）上截取AE＝v_A，并连接CE，令ED＝(Δv)_τ，CE＝(Δv)_n。这样，线速度的速度变化量Δv可分解为(Δv)_τ、(Δv)_n两部分的矢量和，即Δv＝(Δv)_τ＋(Δv)_n。其中（Δv）_τ表示由于线速度大小（即速率）变化引起的速度变化量，而(Δv)_n表示由于线速度方向变化引起的速度变化量。根据加速度的定义得

a＝lim_Δt→0Δv/Δt＝lim_Δt→0(Δv)_τ/Δt＋lim_Δt→0(Δv)_n/Δt。

当Δt→0时，有∠CAE→0，这时(Δv)τ的方向趋于v_A的方向，即A点的切线方向，所以lim_Δt→0(Δv)_τ/Δt表示的分加速度叫做切向加速度，用a_τ表示。大小为

a_τ＝lim_Δt→0(Δv)_τ/Δt＝dv/dt

切向加速度a_τ反映了圆周运动的速度在大小上的变化，或者说是描述由于线速度大小（即速率）的变化而引起的速度变化的快慢（即(Δv)_τ的变化快慢）的物理量。

当Δt→0时，有∠CAE→0，所以底边(Δv)_n与腰v_A垂直，因此lim_Δt→0(Δv)_n/Δt的方向沿半径方向指向圆心，我们称这个分加速度为向心加速度。以a_n表示。大小为

a_n＝lim_Δt→0(Δv)_n/Δt＝lim_Δt→0v_AΔθ/Δt＝v_Aω＝v_A²/R

向心加速度a_n反映了圆周运动的速度在方向上的变化，或者说是描述由于线速度的方向变化而起的那部分速度变化的快慢（即(Δv)_n变化的快慢）的物理量。

质点在A点的加速度a 可以看作a_n与a_τ的矢量和，即

a＝a_n＋a_τ。

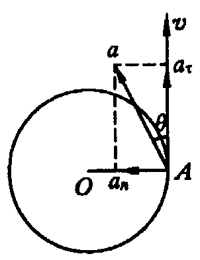式中三者的矢量关系如图4所示。由于a_n 与a_τ方向互相垂直，所以圆周运动的总加速度大小为

a²＝a_n²＋a_τ²

若θ为a与v的夹角，则 θ＝tan^-1(a_n/a_τ )

以上关于加速度的讨论及结果，适用于任何的平面曲线运动。

根据以上分析可知，向心加速度是为了解决一般曲线运动的加速度的求解而引入的，它是描述做圆周运动的质点由于线速度的方向的变化而引起的速度变化快慢的物理量。对于匀速圆周运动，v是常数，所以a_τ＝0，则a＝a_n。因此，匀速圆周运动的向心加速度即为物体的加速度，是描述线速度这个矢量变化快慢的物理量，它的物理意义等同于上述推导的a_n，不应该单纯理解为描述线速度方向变化快慢的物理量。

综合全文的分析，可以得出如下一些结论：

（1）速度方向变化的快慢可以用a_n/v来描述。

（2）对于匀速圆周运动，无论以向心加速度或角速度来描述线速度方向的变化快慢均是不严谨的。且匀速圆周运动的向心加速度即为物体的加速度，是描述线速度这个矢量变化快慢的物理量。

（3）在目前的高中物理教学中，不宜提线速度方向变化快慢的问题来进行讨论。

参考文献：

1．高级中学课本。物理（一年级用）。上海：上海科学技术出版杜。

2．高级中学课本。物理拓展型课程第1册。上海：华东师范大学出版社。

3．张修文。关于向心加速度的辨析。物理教学探讨，2006（5）（上半月）。

4．蒋基豪，吴常光。“关于向心加速度的辨析”质疑。物理教学探讨。2007（2）（上半月）。

5．陈卫东，李俊。顺理不一定成章。中学物理教学参考，2005（4）。

6．张大洪，尹学明。向心加速度是描述什么的7。高中数理化，2007（6）。

7．[美]M.Alonso，E.J.Finn合著，梁宝洪译。大学物理学基础（第1卷）。力学与热力学。北京：高等教育出版社，1983。

8．戴坚舟，刘宝坤，施善定编著。工科大学物理。上海：华东化工学院出版社，1992。

9．张三慧编著。大学基础物理学（上册）。北京：清华大学出版社，2005。

10．罗蔚茵。力学简明教程。广州：中山大学出版社，1985。

发布时间：2010/3/12 下午4:46:05  阅读次数：13618