点电荷间相互作用力的探索过程及启示

甘肃省武威市武威二中 王惠芳 选自《中学物理教学参考》2009年第5期

我们已经知道，自然界中存在两种电荷，那么电荷之间相互作用力的大小跟哪些因素有关呢？科学家们是怎样研究的？了解这一过程会让我们受到很多启示。

一、点电荷间相互作用的早期研究

早在公元前五世纪的希腊时代，就有了关于静电现象的历史记载。我国西汉末年就有经过摩擦的玳瑁能够吸引微小物体的记载。但直到1660年，盖里克发明了摩擦起电机后，人们才真正开始了对电现象的详细观察和细致研究。

1733年，杜菲（Du Fay，1698～1739）经过实验区分出两种电荷，并由此总结出静电作用的基本性质：同性相斥，异性相吸。

二、对点电荷间相互作用的各种猜测

到18世纪中叶，牛顿力学已经取得辉煌胜利，人们借助于万有引力定律，对电场力和磁场力作了种种猜测。

1．爱皮努斯（F．U．T．Aepinus，1724～1802）的假说

德国柏林科学院院士爱皮努斯1759年对电场力作了研究。他在书中假设电荷之间的斥力和引力随带电物体间距离的减少而增大，从而对静电感应现象作出了更完善的解释。不过，他并没有实际测量电荷间的作用力，因而这个观点只是一种猜测。

2．D．伯努利的假说

在1760年，D．伯努利首先猜测电场力会不会也跟万有引力一样，服从平方反比规律。他的想法显然有一定的代表性，因为平方反比规律在牛顿的形而上学自然观中是很自然的观念。

3．普利斯特利（Priestley，1733～1804）的假说

1755年，富兰克林在空罐实验（也叫冰桶实验）中观察到这样一种现象：“把一只品脱银罐放在电支架（即绝缘支架）上，使它带电，用丝线吊着一个直径约为1英寸的木髓球，放进银罐中，直到触及罐的底部。但是，当取出木髓球时，却发现接触没有使它带电，像从外部接触的那样。”

当时，没有人能解释这种现象。后来，富兰克林写信告诉他的朋友普利斯特利这一实验现象并向他求教。普利斯特利是位化学家，对电学也很有研究。普利斯特利重复做了富兰克林的空罐实验，最后，他从这个实验中得出：“电的吸引力与万有引力服从同一规律，即平方反比规律。因为很容易证明，假如地球是一个球壳，在壳内的物体受到一边的吸引作用，决不会大于另一边的吸引。”

普利斯特利的这一结论并不是凭空想出来的，因为牛顿早在1687年就证明过，如果万有引力服从平方反比规律，那么均匀的物质球壳对壳内物体应无作用。不过，普利斯特利的结论并没有得到科学界的普遍重视，因为他并没有特别明确地进行论证，仍然只停留在猜测阶段。

三、点电荷间相互作用的定量研究

尽管这时人们对电的认识有了初步的成果，但是，如果不建立定量的规律，电的知识还不能形成一门严密的科学。后来，科学家们沿着这个思路开始了对点电荷间相互作用的定量研究。

1．罗宾森（John Robison，1739～1805）的实验研究

1759年，罗宾森从爱皮努斯的著作中了解到他对电场力的猜测。他对此很感兴趣，就设计了一个杠杆装置。装置利用活动杠杆所受重力和电场力的平衡，从支架平衡的角度求电场力与距离的关系。他确定了同种电荷间的斥力反比于电荷间距的2.06次幂，异种电荷间的吸引力反比于电荷间距的小于2的次幂。他认为，指数有偏差的原因是由于实验误差。由此，他得到结论：电场力服从平方反比规律。可惜，他的实验结果因没有及时发表而未对科学的发展起到应有的推动作用。

2．卡文迪许（Hrmry Cavendish，1731～1810）的实验研究

英国的卡文迪许考虑到电场力和万有引力的相似性，设想有一薄球壳，在它表面上有均匀分布的电荷，在这个球壳内放入一个电荷，若电荷之间的相互作用力反比于它们之间距离的平方，那么根据引力的讨论可以得知，整个球壳上均匀分布的电荷对该电荷总作用力的合力为零。

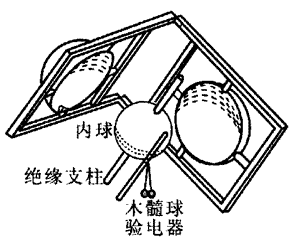1773年，卡文迪许用两个同心金属球壳做实验，外球壳由两个半球组成，两半球合起来正好形成内球的同心球。卡文迪许这样描述他的装置（如图1所示）：

“我取一个直径为12.1英寸的球，用一根实心的玻璃棒穿过其中心当做轴，并覆盖以封蜡……然后把这个球封在两个中空的半球中间，半球直径为13.3英寸，1.20英寸厚……然后，我用一根导线将莱顿瓶的正极接到半球，使半球带电。”卡文迪许通过一根导线将内外球连在一起，外球壳带电后，取走导线，打开外球壳，用木髓球验电器试验内球是否带电。结果发现木髓球验电器没有指示，证明内球没有带电，电荷完全分布在外球上。卡文迪许将这个实验重复了多次，确定了电场力服从平方反比规律，其指数偏差不超过2％。

卡文迪许这个实验的设计相当巧妙。他用的是当年最原始的测电仪器，却获得了相当可靠而且精确的结果。该实验比库仑用扭秤测电场力的实验早11年，而且结果更为精确。该结果在1744年前就已完成，但直到19世纪中叶，开尔文在卡文迪许的手稿中才发现，1879年才由麦克斯韦整理发表，这实在是科学史上的一大遗憾。

3．库仑（Coulomb，1736～1806）的实验研究

法国物理学家库仑在研究点电荷之间的相互作用时，把类比的方法发挥得淋漓尽致。

（1）同种电荷间的相互作用

库仑早年从事摩擦及扭转的研究，发现了金属丝的扭力定律，得出了力与扭转角成正比的规律。另外，他还发明了扭秤，它能测量极小的力，其精度可达到10－8N。库仑就用它来测量电荷之间的排斥力与电荷间距离的关系。

通过实验，库仑得出结论：“两个带有同种类型电荷的小球之间的排斥力与这两小球中心之间距离的平方成反比。”但库仑的实验结果精确度并不很高，其指数偏差可达4％。那么，他为何不用F∝1/R^2.04或F∝1/R^1.96 的形式发表自己的结论呢？据史料记载，库仑借鉴了万有引力定律，事先有了平方反比的概念，才会得出这样的结论。

另外，库仑并没有进行改变电量的实验，而是说：“假说的前一部分无需证明”。显然他是在模仿万有引力定律，因为万有引力是与相互作用的两物体的质量成正比的。

（2）异种电荷间的相互作用

对于异种电荷之间引力与电荷间距离的关系，用扭秤实验研究遇到了很大的困难。经过不断探索，库仑从力学的单摆实验中得到启发来解决这个问题。在这之前人们已经知道，地球上的物体都受到地球引力的作用，引力的大小与物体和地球中心之间距离的平方成反比。若把地球视作一个质量集中在其中心的质点，地球上悬挂的物体绕其悬点作微小摆动时，其振动周期T与物体到地球中心的距离R成正比，即T∝R。库仑设想，如果异种电荷之间的引力也服从平方反比规律，那么只要设计一种电摆就可以进行实验了。库仑通过改变距离，测量振动周期，得出距离之比为3∶4∶8，振动周期之比为20∶41∶60。如果按平方反比规律，则振动周期之比应为20∶40∶54。考虑到漏电等因素，修正后的实验值与平方反比规律得出的值已经很接近了。这里他仍然借鉴了万有引力定律，最后库仑确定不论同种电荷还是异种电荷，它们之间作用力的大小均符合与距离平方成反比的规律。

四、现在的观点

鉴于库仑总结出的平方反比规律所依据的实验精度不高，而库仑定律是电磁学的基本定律，是否精确地满足平方反比关系又至关重要，所以从库仑定律发表以后直到现代，科学家们用越来越精确的实验来验证平方反比规律，也就是检验距离r的方次与“2”之间究竟有多大偏差。1971年的实验表明，这个偏差如果有，也不会大于3×10^－16。可见，库仑定律是一个经过实验检验的精确度极高的物理定律。

五、启示

从库仑定律的发现经过我们可以看到假说和类比的方法在科学研究中所起的重要作用。假说是对自然现象有根据的推测，假说的不断修正、补充和更新，会更多地、更正确地反映客观现实的某些方面。因此，它是人们的认识向客观真理接近的有效方式。类比的方法指通过活化人们头脑中储存的知识信息，找出一些表面上不相关联的对象之间共性的方面，这种方法在科学研究中占有很重要的地位。

由此可见，库仑定律的建立既是实验经验的总结，又是理论研究的成果。如果不是先有万有引力定律的发现，单靠具体实验数据的积累，不知要到何时才能得到严格的库仑定律的表达式。

总之，教师在教学过程中要充分挖掘物理教材中蕴含的物理方法教育的素材，在知识教学的同时讲授方法，启示学生思考和领悟，从而逐步培养学生良好的思维品质，提高学生分析问题和解决问题的能力。

发布时间：2010/1/11 上午8:30:30  阅读次数：16732