第二章D 共点力的平衡教学建议

（一）学习目标

1．理解共点力平衡的概念和条件；会用力的合成与分解方法求解简单的共点力平衡问题。

2．感受处理共点力平衡问题的分析过程，能运用数学中建立直角坐标系和三角函数关系等方法解决共点力平衡问题。

3．感悟共点力平衡的实际应用价值。

（二）重点和难点

本节重点是共点力平衡的条件及应用。

本节难点是分析和解决共点力平衡的实际问题。

（三）教学建议

本节教材首先创设了神舟号飞船返回舱的种种平衡状态的情景，然后引导学生学习共点力平衡的特点和条件。既贴近了时代，贴近了实际，又能激发学生的民族自豪感，为课堂教学创设了一个广阔的科技背景。接着从学生已有的二力平衡知识出发讨论i力平衡问题，从平衡状态到平衡条件再到实际应用。教材的示例编写中还考虑到用多种方法解题，在这里将力的合成和分解知识与共点力平衡的条件结合起来运用，对学生来说，解题的能力又有了飞跃。其中还应用共点力平衡原理去解决返回舱在海面降落时的回收问题。这些都体现了新教材的特点。

本节内容建议安排2课时，第1课时学至示例1，第2课时为习题课。

1．关于共点力平衡的教学建议

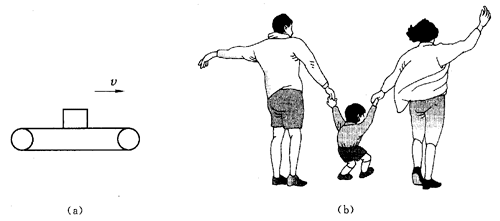
首先要明确的是：物体处于静止或匀速直线运动状态都属于平衡状态。建议讲完共点力平衡之后再回过头来举例说明关于平衡状态的问题。如图18（a），匀速前进的传送带上的物体，只受到两个力的作用；图18（b）中，父母提着小孩匀速前进，小孩也只受三个力的作用（空气阻力不计）。

教材中图2-44和图2-45表明：物体平衡时合力必定为零。图2-45更是将不平衡到新的平衡这个过程表达了出来。这里还应说明多个共点力作用于一个物体，处于平衡状态时，最终都可以归结到二力平衡，合力为零。

2．关于“示例”的教学建议

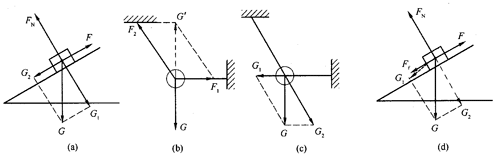
教材中示例1采用的是F与G的合力与FN相平衡来解题，而不是将F与FN的合力与G平衡来解，是为了告诉学生三力平衡时，“任意两个力的合力都等于第三个力”，各种解法都可以运用。而“想一想”是要求学生还可考虑到用分解的办法来处理，如图19（a）所示，将重力正交分解就是一例。这里还可以安排一些“自主活动”，补充一些巩固性的练习，如图19（b）所示。值得注意的是用共点力平衡方法画出的受力图与用重力分解方法作出的受力图是不同的，前者是以物体为对象进行受力分析，然后再行解题；后者是以重力作用下对两根绳子产生的效果进行分解来解题的，如图19（c）所示，这时受分力作用的对象是绳子，不是球，但两种解法的结果是相同的。在只有两个分力的情况下，用分解方法，有时比较简捷；但物体受力较多的情况下，用共点力平衡的方法比较妥当。对学生来说，一旦掌握熟练之后，常常会把共点力平衡的方法与力的分解的方法结合起来运用，做到游刃有余。如图19（d）所示，斜面上木块在推力作用下向上运动，还受到摩擦力的作用，一般总是先进行受力分析，将各个共点力都画出来，然后将重力分解后进行解题。这种情况要随学习内容的深入，再与学生逐步讨论，对初学者来说，不宜讲得太复杂。

3．关于本节最后部分的教学建议

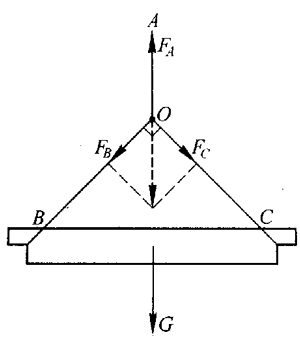
本节的最后还可以回头来讨论一下本章导言中东海大桥建设时大型吊车吊起200t横梁的事例，假设钢绳OB与OC夹角为90°（图20），则它们承受的拉力是多大？从整体来看，由于两力平衡，钢绳OA的拉力为200t，即2×10⁶N，F_A、F_B、F_C为共点力，可以求得F_B＝F_C＝×10⁶N即1.4×10⁶N。可以告诉学生，实际上单根钢绳无法承受这么大的力。通常在悬吊时用多根悬绳来分担。

（四）作业说明

本节共有练习题10道，如果按2课时教学，建议第1课时布置第1～5题，其余题在第2课时布置。

参考答案如下：

A组

1．mgcosθ mgsinθ 方向略

2．10N 方向与8N的力成143°

3．A组能平衡，B组不能平衡。A组中两个较小的力相加大于最大的力，总合力可为零，B组则不能

4．还应加18N的力与原9N力的方向一致

5．（1）12.5N （2）7.5N

6．减小 减小

7．C

8．OP部分先断裂 0P与竖直方向夹角为60°

B组

9．C

10．G/3

发布时间：2009/11/25 上午9:23:55  阅读次数：5058