第二章B 力的合成教学建议
（一）学习目标
1．知道共点力，理解力的合成概念；理解平行四边形定则，会用作图法或解直三角形法求合力；会用橡皮筋、弹簧测力计等实验器材研究合力与分力的关系。
2．通过实验探究过程学习平行四边形定则；认识力的合成是一种等效替代方法；感受矢量与标量的求和方法。
3．通过有关力的合成的实际事例分析，感悟力的合成在桥梁、工地及日常生活中的实际意义和应用价值。
（二）重点和难点
本节重点是互成角度的两个力的合成及平行四边形定则。
本节难点是对平行四边形定则的探究及运用该定则解题。
（三）教学建议
本节教材的编写从古代拔鼎故事引入，目的是引发对所讨论问题的兴趣，也体现了科学与人文的结合。然后用大桥斜拉索说明等效替代的概念，进而通过实验探究得出力合成的平行四边形定则。最后通过示例对该定则加以应用。比较典型地体现了本教材“情景－探究－应用”的特点。
本节建议用2课时完成，第1课时完成探究实验，第2课时学习示例并做一些有关的训练。
1．关于“引入”部分的教学建议
“泗水拔鼎”这篇古文可先让学生阅读一下，在分析当时拔鼎情景时，可以让学生想像，系在鼎的绳索可能是怎样的？是斜向的，向四周的，而不是竖直向上的，拉的效果呈相互抵消状态，学生可能会说出“不能形成合力”等话语，当然更符合本节的要求；另一方面，学生可能会考虑到陷于沙泥中的鼎，底部排除水后，大气压力紧紧将它压在河底，如同一个马德堡半球，若鼎的横截面积以0.5m2计算，大气压力可达5×104N（约相当于质量为5t的物体产生的重力），这也是难以拔起的原因之一。
下面图10是当时拔鼎时情景的示意图，可以帮助学生理解石刻中的内容。
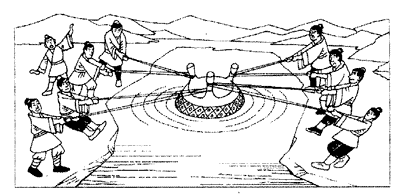
2．关于“力的合成”的教学建议
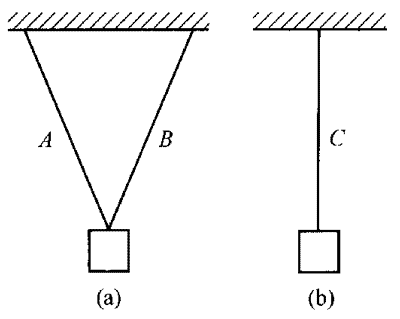
杨浦大桥的案例突出了等效思想，但要注意，“等效”不等于“等同”，“等效”只是在某一方面，某一方向上的效果相同，它不代表所有的情况下都相同。如图11所示，重物用A、B两根绳子系住，也可以用一根绳C替代两根绳将它系住，这只是在竖直方向上是等效的；当有水平向左的力作用于物体时，这两种情况下物体的运动情况不同，是不等效的。
教材58页“点击”中是将共点力的概念适当扩展，这对解决实际问题相当有用，可以让学生自学，不必花过多时间展开。
3．关于“学生实验”的教学建议
“探索研究”之前先复习初中学过的同一直线上两力合成知识，再提出不在一直线上的两个共点力怎样合成？要求学生先猜想，如果学生猜出“平行四边形对角线”，那么实验变成为验证，这也是一种探究，关键是怎样用等效替代方法来得到“平行四边形定则”。实验步骤一定要学生自己通过讨论确定，然后进行操作，一般地说，步骤（1）：用两个弹簧测力计互成角度地拉绳套，使橡皮筋伸长到一定的位置，记下这个位置，画出弹簧测力计方向，记录示数F1和F2。步骤（2）：用一个弹簧测力计代替原来两个弹簧测力计将橡皮筋拉伸到原来位置，记下示数F和方向。步骤（3）：用画力的图示方法，取单位线段，画出F1和F2及F，将F1和F2为邻边画出平行四边形，得到其对角线F'，看看F'与F是否完全重合。改变两力的夹角再做一次实验，并得出结论，最后才总结出平行四边形定则。
这个实验要求学生规范地操作。学生易犯的毛病是：力的作用线画得不准确；读数时手按住结点；两次拉结点不达同一点等。此外还有凑数据现象。
为此，要进行认真仔细、实事求是的思想教育。
4．关于“自主活动”的教学建议
教材60页的“自主活动”要求做一个平行四边形支架，可以发给学生器材，当场组装。
若时间紧，可作为课外作业，自找材料（纸板即可）完成。这里主要应强调矢量加法与标量加法是不同的。
这里可以补充一个练习：两个大小均为5N的共点力合成后，最小值和最大值为多大？它们夹角多大时，合力等于分力？合力与其中一个分力间最大夹角是几度？
答案：0和10N，120°，接近90°。
（四）作业说明
本节共有练习题11道，如果按2课时教学，第1课时可布置第1～5题，第2课时布置其他各题。其中11题作为选做题。
参考答案如下：
A组
1．合 分
2．D
3．F合＝0.45N tanθ＝1/2 θ＝26.6°（可从计算器上求得）
4．合力为3300N（作图求得）
5．B
6．0 50
7．7 1 5
8．略
B组
9．100 100
10．6N（F1与F5合力为1N，F2为2N，F2与F4合力为3N）
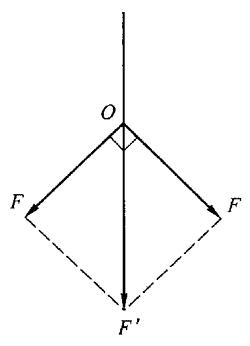
11．本题既有实际意义，又不是能直接得到结果，有一定的难度。首先要分析出绳的拉力F'可看成是OA与OB绳拉力F的合力（从图上看出OA与OB与OC是对称的，即OA与OB拉力相同）。从图12上可以看出，F'＝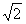
F，所以F'/F ＝
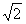。设绳的半径分别为r'和r，横截面积分别为S'、S。则F'/F ＝S'/S ＝πr'2/πr2
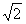＝r'2/r2 ＝ ，所以r'/r
≈1.2。即OC绳的直径约是OA、OB绳直径的1.2倍
发布时间：2009/11/23 上午10:03:21 阅读次数：4817
