5.9 使用双线性插值计算地形的精确高度

问题

当你制作一个使用地形的游戏时，你需要知道地形确定点的精确高度。例如，在地形上移动一个模型时(见教程4-17)，当检测到光标和地形之间的碰撞时（下一个教程），或防止相机与地形碰撞时（见教程2-6）。

因为在前一个教程中你定义了地形每个顶点的3D位置，所以获取这些点的高度很简单。对位于这些顶点间的位置而言，你需要使用一种插值方法获取这个位置的精确高度。

解决方案

如果你想知道高度的点与地形的一个顶点发生碰撞，那么你已经知道了地形上该点的精确高度。如果这个点并没有与顶点发生碰撞，那么说明这个点在地形的一个三角形上。因为三角形是一个平面，所以你可以通过在三角形三个顶点间进行插值获取任何点的精确高度。

工作原理

首先从X和Z坐标开始，你想知道该点的对应Y坐标，这可以通过对三角形三个顶点的高度进行插值获取。

这意味着你首先要找到点究竟在哪个三角形中，这并不容易。但首先我想介绍插值。

线性插值

如果你只处理分离的数据、想知道分离点之间的某些值，需要用到某种类型的插值。这种情况如图5-17坐标所示。对某些分离的(整数) X值，你知道Y值。当X=2，你知道Y=10，X=3时Y=30。但你不知道X=2.7时的Y值。

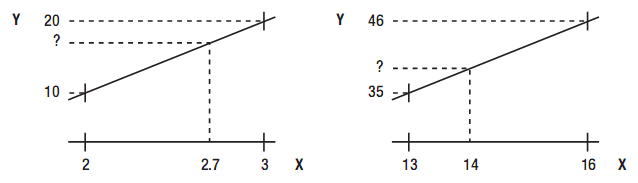
使用线性插值，你通过连接两点的线段找到X=2.7对应的Y值，如图5-17所示。使用线性插值，通过连接两点的线段找到X=2.7对应的Y值。线性插值总是将X表达成0和1之间，0对应X的最小值（你知道对应的X值，本例中为2），1对应X的最大值（本例中为3）。本例中你想找到X=2.7时的Y值，结果是0.7，意思是“2和3至之间的70%。”

在图5-17的左图中，0%对应Y值10，100%对应Y值20，所以70%对应Y=17。这很容易看出，但右图的情况如何？14对应0.33，因为它是13和16之间的33%。但35和46之间的33%是多少？显然，你希望有代码可以为你计算结果。

首先要有代码找到0和1对应的值。从X值开始，首先减去最小的X值，这样最小值变为0。然后，将最大值缩放为1，你可以通过将它除以最大值和最小值之差实现。

下面是图5-17左图的做法： 2.7→(2.7－min)/(max－min)=(2.7－2)/(3－2)=0.7

然后，进行逆运算获取对应的Y值：首先缩放这个值(通过乘以最大值和最小值的差值)，并加到最小的Y值上：

0.7* (maxY－min Y)＋minY=0.7*(20－10)＋10=0.7*10＋10=17

这里你采取图5-17左图简单例子的规则，但你可以使用这个方法计算任何线性插值。看一下图5-17右图更难的例子，在这种情况中，你知道X=13对应Y=35，X=16对应Y=46，但你想知道X=14对应的Y值。所以，首先获取0和1之间对应的值：

14→(14－minX)/(maxX－minX) =(14－13)/(16－13)=0.33

知道了对应值，就做好了获取对应Y值的准备：

0.33* (maxY－minY)＋minY=0.33*(46－35)＋35=0.33*11＋35=3.67＋35=38.67

最后，需要进行浮点计算。图5-17的右图中找到X=14对应Y=38.67。事实上，几乎所有插值计算都返回一个浮点数。

技巧：XNA提供了一个功能可以为你计算Vector2, Vector3或Vector4的插值。例如，如果你想获取哪个Vector2位于(5,8)和(2,9)之间的70%，你可以使用Vector2. Lerp(new Vector2(5,8), new Vector2(2,9), 0.7f)。

双线性插值

在地形的例子中，对所有(X,Z)值，你已经定义了一个顶点并知道了它的精确高度。对所有在这些独立顶点之间的(X,Z)值，你不知道精确的Y值，所以需要进行插值。这次你需要获取0和1之间的值，包含X和Z。

有了这些值，就可以分两步计算出精确的Y值。

获取对应值

给定任意(X,Z)坐标，你需要找到地形上的精确Y高度。首先使用前面的公式找到对应的X和Z值，但这次因为在3维空间中，你需要用两次：

int xLower = (int)xCoord; 
int xHigher = xLower + 1; 
float xRelative = (xCoord - xLower) / ((float)xHigher - (float)xLower); 
int zLower = (int)zCoord; 
int zHigher = zLower + 1; 
float zRelative = (zCoord - zLower) / ((float)zHigher- (float)zLower);

在地形中每个X和Z的整数值你定义了一个顶点，所以你知道精确的Y值。所以对每个X的浮点数，你要将它们转换为整数获取最小的X值(例如，2.7变为2)。将这个值加1获取最大X值(2.7对应3作为最大值)。知道了边界，很容易使用前面的公式找到对应值。Z值的求法类似。

获取minY和maxY的值

知道了0和1之间的对应值，下一步是找到精确Y值。但是，首先需要知道minY和maxY值。这些值表示顶点中的高度。你需要知道点在哪个三角形中才能知道使用哪个顶点的高度作为Y值。

你知道点P的X和Z坐标，所以你知道点周围的四个顶点，很容易获取它们的Y值：

float heightLxLz = heightData[xLower, zLower]; 
float heightLxHz = heightData[xLower, zHigher]; 
float heightHxLz = heightData[xHigher, zLower]; 
float heightHxHz = heightData[xHigher, zHigher];

LxHz表示“低X坐标，高Z坐标” 决定(X,Z)。

点在哪个三角形中用来绘制地形的两个三角形。有两个方式可以定义这两个三角形，如图5－18所示。绘制三角形的方式影响到P点的高度，如图所示。

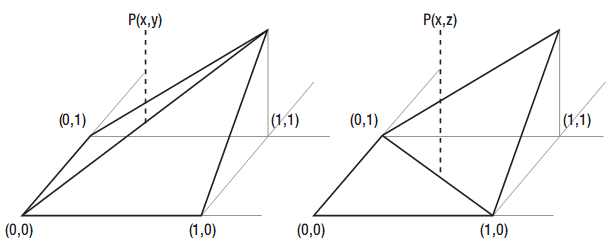
图5-18 从四个顶点绘制两个三角形的两种方法

虽然四个顶点有相同的坐标，但两种情况中的点的高度并不相同，图中你可以可出明显的区别。

基于我即将讨论的理由，更好的方式是图5－18的右图。

使用这个旋转方式，很容易确定点在哪个三角形上方。两个三角形之间的边界由对角线给出。在右图中，如果xRelative + zRelative 为1的话，这条线对应具有X和Z坐标的点。

例如，如果这个点在四个点中央，如图5－18所示，xRelative和zRelative都是0.5f，所以和为1，说明在对角线上。如果这个点偏向左边一点，xRelative会小一些，和会小于1，对Z坐标也是类似的情况。所以如果和小于1，(X,Z)坐标位于左下角的三角形内；否则，该点在右上角的三角形内：

bool pointAboveLowerTriangle = (xRelative + zRelative < 1);

注意：图5－16中定义的所有三角形都是以图5－18右图中的形式绘制的。

获取精确高度

知道了对应高度，四个周围顶点的高度和点位于哪个三角形中，你就可以计算精确高度了。

如果点在左下方的三角形中，这时pointAboveLowerTriangle为true，下面是使用双线性插值获取三角形任意点高度的代码：

finalHeight = heightLxLz; 
finalHeight += zRelative * (heightLxHz - heightLxLz); 
finalHeight += xRelative * (heightHxLz - heightLxLz);

根据前面解释的单插值的方法，从lowestX的Y值开始。因为这是“双”插值，你要从lowestXlowestZ的Y值开始。

在单插值中，你maxY之间添加高度差，并乘以对应的X值。在双插值中，你乘的是 zRelative和xRelative。

换句话说，从左下顶点的高度开始，对这个高度，你添加了这个顶点和有着更高Z坐标的顶点间的高度差，并乘以距离第二个顶点的Z坐标的接近程度。最后一行代码类似：对这个高度，你添加了左下顶点和右下顶点的高度差，乘以距离右下顶点的X坐标的接近程度。

如果该点在右上三角形的内部，这时pointAboveLowerTriangle为false，情况有所不同，你需要以下代码：

finalHeight = heightHxHz; 
finalHeight += (1.0f - zDifference) *(heightHxLz - heightHxHz); 
finalHeight += (1.0f - xDifference) * (heightLxHz - heightHxHz);

从高度开始，从右上顶点开始，遵循同样的步骤：添加高度差，乘以对应距离。

代码

这个方法包含前面解释的所有代码。基于任意(X,Z)坐标，无论是整数还是浮点数，这个方法返回该点的精确高度。首先检查该点是否在地形上。如果不是，返回默认的高度10。

public float GetExactHeightAt(float xCoord, float zCoord) 
{
    bool invalid = xCoord < 0; 
    invalid |= zCoord < 0; 
    invalid |= xCoord > heightData.GetLength(0) - 1; 
    invalid |= zCoord > heightData.GetLength(1) - 1; 
    
    if (invalid) 
        return 10; 
    
    int xLower = (int)xCoord; 
    int xHigher = xLower + 1; 
    float xRelative = (xCoord - xLower) / ((float)xHigher - (float)xLower); 
    int zLower = (int)zCoord; 
    int zHigher = zLower + 1; 
    float zRelative = (zCoord - zLower) / ((float)zHigher - (float)zLower); 
    float heightLxLz = heightData[xLower, zLower]; 
    float heightLxHz = heightData[xLower, zHigher]; 
    float heightHxLz = heightData[xHigher, zLower]; 
    float heightHxHz = heightData[xHigher, zHigher]; 
    
    bool pointAboveLowerTriangle = (xRelative + zRelative < 1); 
    float finalHeight; 
    if (pointAboveLowerTriangle ) 
    { 
        finalHeight = heightLxLz; 
        finalHeight += zRelative * (heightLxHz - heightLxLz); 
        finalHeight += xRelative * (heightHxLz - heightLxLz); 
    }
    else 
    {
        finalHeight = heightHxHz; 
        finalHeight += (1.0f - zRelative) * (heightHxLz - heightHxHz); 
        finalHeight += (1.0f - xRelative) * (heightLxHz - heightHxHz); 
    }
    return finalHeight; }

发布时间：2009/9/16 上午11:39:59 阅读次数：8219