杨氏双缝干涉条纹间距到底是不是相等的?
海军航空工程学院 李磊 梁吉峰 选自《物理教师》2008年第11期
在杨氏双缝干涉实验中,在现行的高中物理教科书中得出相邻的明纹(或者暗纹)中心间距为:\(\Delta x = \frac{L}{d}\lambda \),其中 L 为双缝与屏的间距,d 为双缝间距,对单色光而言,其波长 λ 为定值,所以我们得出的结论是干涉图样为等间距的一系列明暗相同的条纹,但是在现行的高中物理教科书中所给的干涉条纹的照片却并非如此,如图 1。我们可以看到只是在照片中央部分的干涉条纹是等间距的,但是在其边缘部分的条纹的间距明显与中央部分的条纹间距不同。问题到底出在哪里呢?

首先我们来看现行的教科书上对于杨氏双缝干涉的解释,如图 2。
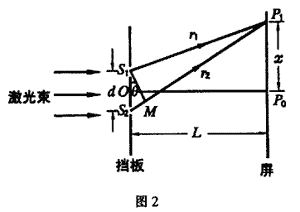
设定双缝 S1、S2 的间距为 d,双缝所在平面与光屏 P 平行。双缝与屏之间的垂直距离为 L,我们在屏上任取一点 P1,设定点 P1与双缝 S1、S2 的距离分别为 r1 和 r2,O 为双缝 S1、S2 的中点,双缝 S1、S2 的连线的中垂线与屏的交点为 P0,设 P1 与 P0 的距离为 x,为了获得明显的干涉条纹,在通常情况下 L ≫ d,在这种情况下由双缝 S1、S2 发出的光到达屏上 P1 点的光程差 Δr 为
\({S_2}M = {r_2} - {r_1} = d\sin \theta \) (1)
其中 θ 也是 OP0 与 OP1 所成的角。因为 d ≪ L,θ 很小,所以
\(\sin \theta \approx \tan \theta = \frac{x}{L}\) (2)
因此 \(\Delta r \approx d\sin \theta \approx d\frac{x}{L}\)。
当 \(\Delta r \approx d\frac{x}{L} = \pm k\lambda \)时,屏上表现为明条纹,其中 k = 0,1,2,……, (3)
当 \(\Delta r \approx d\frac{x}{L} = \pm (k + \frac{1}{2})\lambda \)时,屏上表现为暗条纹,其中是 k = 0,1,2,……。 (3′)
我们继续算得光屏上明条纹和暗条纹的中心位置。当 \(x = \pm k\frac{L}{d}\lambda \) 时,屏上表现为明条纹,其中 k = 0,1,2,…。 (4)
当 \(x = \pm (k + \frac{1}{2})\frac{L}{d}\lambda \)时,屏上表现为暗条纹,其中 k = 0,1,2,…。 (4′)
我们还可以算出相邻明条纹(或者暗条纹)中心问的距离为
\(\Delta x = {x_{k + 1}} - {x_k} = \frac{L}{d}\lambda \) (5)
至此我们得出结论:杨氏双缝干涉条纹是等间距的。
问题就在于以上的推导过程中,我们用过两次近似,第 1 次是在运用公式 Δr= r2-r1 ≈ dsinθ 的时候,此式近似成立的条件是 ∠S1P1S2 很小,因此有 S1M⊥S2P1,S1M⊥OP1,因此 ∠P0OP1=∠S2S1M,如果要保证 ∠S1P1S2 很小,只要满足 d≪L 即可,因此 Δr≈dsinθ 是满足的。
第 2 次近似是因为 d≪L,θ 很小,所以 sinθ ≈ tanθ。下面我们通过表 1 来比较 sinθ 与 tanθ 的数值。
表1
| θ | 1° | 2° | 3° | 4° | 5° | 6° |
| sinθ | 0.017452 | 0.034899 | 0.052359 | 0.069756 | 0.087155 | 0.104528 |
| tanθ | 0.017455 | 0.034920 | 0.052407 | 0.069926 | 0.087488 | 0.105104 |
| θ | 7° | 8° | 9° | 10° | 11° | |
| sinθ | 0.121869 | 0.139173 | 0.156434 | 0.173648 | 0.190808 | |
| tanθ | 0.122784 | 0.140540 | 0.158384 | 0.176326 | 0.194380 |
从表 1 中我们可以看出当 θ=6° 时,\(\frac{{\tan \theta - \sin \theta }}{{\sin \theta }}\) ≈ 0.6%。因此当 θ ≥ 6° 时,相对误差就超过了 0.6%,因此我们通常说 sinθ = tanθ 成立的条件是 θ ≤ 5°,当 θ > 5° 时,sinθ ≈ tanθ 就不再成立。而在杨氏双缝干涉实验中,θ 很小所对应的条件应该是 x ≪ L,这应该对应于光屏上靠近 P0 的点,在此种情况下上述的推导过程是成立的,干涉条纹是等间距的。
而当 x 较大时,也就是光屏上离 P0 较远的点所对应的 θ 角也较大,当 θ > 5° 时,sinθ ≈ tanθ 就不再成立,上述推导过程也就不完全成立了,(2)式就不能再用了。
此时 \(\sin \theta = \frac{x}{{\sqrt {{L^2} + {x^2}} }}\)
所以,\(\Delta r = d\sin \theta = \frac{{dx}}{{\sqrt {{L^2} + {x^2}} }} = \pm k\lambda \),屏上表现为明条纹,其中 k = 0,1,2,…,
\(\Delta r = d\sin \theta = \frac{{dx}}{{\sqrt {{L^2} + {x^2}} }} = \pm (k + \frac{1}{2})\lambda \),屏上表现为暗条纹,其中 k = 0,1,2,…。
因此可以得到光屏上明纹或者暗纹的中心位置为 \(x = \pm \frac{{Lk\lambda }}{{\sqrt {{d^2} - {k^2}{\lambda ^2}} }}\) ,屏上表现为明条纹,其中 k = 0,1,2,…,
\(x = \pm \frac{{L(k + \frac{1}{2})\lambda }}{{\sqrt {{d^2} - {{(k + \frac{1}{2})}^2}{\lambda ^2}} }}\),屏上表现为暗条纹,其中 k = 0,1,2,…。
则相邻的明条纹中心间距为
Δx明 = xk+1明 一 xk明 = \(\frac{{L(k + 1)\lambda }}{{\sqrt {{d^2} - {{(k + 1)}^2}{\lambda ^2}} }} - \frac{{Lk\lambda }}{{\sqrt {{d^2} - {k^2}{\lambda ^2}} }}\)
邻暗条纹中心间距为
Δx暗 = xk+1暗 一 xk暗 = \(\frac{{L(k + 1 + \frac{1}{2})\lambda }}{{\sqrt {{d^2} - {{(k + 1 + \frac{1}{2})}^2}{\lambda ^2}} }} - \frac{{L(k + \frac{1}{2})\lambda }}{{\sqrt {{d^2} - {{(k + \frac{1}{2})}^2}{\lambda ^2}} }}\)
由上式可见相邻的明、暗条纹就不再是等间距的了,这也正如教科书上的照片所示的条纹分布。
下面我们通过一个实例来定量计算等间距条纹的条数。
例 1:用氦氖激光器(频率为 4.74×1014 Hz)的红光照射间距为 2mm 的双缝时,试求我们能观察到的等间距的条纹的条数。
解:因为 \(\Delta r = d\sin \theta = k\lambda \),所以
\[k = \frac{{d\sin \theta }}{\lambda } = \frac{{\nu d\sin \theta }}{c} = \frac{{4.74 \times {{10}^{14}} \times 2 \times {{10}^{ - 3}} \times \sin 5^\circ }}{{3.0 \times {{10}^8}}} \approx 2.8\]
考虑到光屏的两侧,我们最终能够在光屏上观察到的等间距的条纹大致为 5 条。
文件下载(已下载 3164 次)发布时间:2009/6/26 上午9:15:50 阅读次数:39420
