月球的运动——从一道高考题谈起

福建南安国光中学 刘怀敏 选自《物理教师》2008年第12期

2008年全国理综（卷Ⅰ）第17题出现了以月球运动为背景的一道题。一时间关于月球的运动引发了众多师生的讨论，大家纷纷提出了自己的看法。高考原题如下：

已知太阳到地球与地球到月球的距离的比值约为390，月球绕地球旋转的周期约为27天。利用上述数据以及日常的天文知识，可估算出太阳对月球与地球对月球的万有引力的比值约为（ ）

（A）0.2         （B）2         （C）20            （D）200

此题提供的答案为（B）。一般考生会利用地球绕太阳旋转一周365天，把地球绕太阳旋转和月球绕地球旋转作为匀速圆周运动，它们相互间万有引力提供向心力来处理。由

GM₁M₂/R² ＝M₂4π²T²/R，GM₂M₃/r² ＝M₃4π²t²/r

式中M₁为太阳质量，M₂为地球质量，R为日地距离，T为地球绕太阳旋转一周所用时间；M₃为月球质量，r为月地距离，t为月球绕地球旋转一周所用时间。由于地球到月球距离比起太阳到地球距离来说小很多，因此太阳到月球距离可认为约和太阳到地球距离相等。由万有引力公式。联立上述两式得：

F₁/F₂ ＝M24π²R/T²  / M₃4π²r/t² ＝Rt²/rT²

将太阳到地球与地球到月球的距离的比值约为390，t为27天，T为365天代入（若考虑到为估算题，为计算方便，可用360代入），即可得出答案约为2，选（B）。至此本题圆满解决。

但马上有人提出异议，不对！我们计算时把月球绕地球的运动看成绕地球球心的匀速圆周运动，即认为是地球对月球的万有引力来提供向心力。我们处理问题的前提是忽略了太阳对月球的万有引力，而结果却是太阳对月球的万有引力为地球对月球的万有引力的2倍，结论反过来说明了前提的错误！逻辑自相矛盾。如果结论是正确的，那地球和太阳两者对月球的万有引力的合力怎么可能始终指向地球，从而使月球绕地球作匀速圆周运动呢？

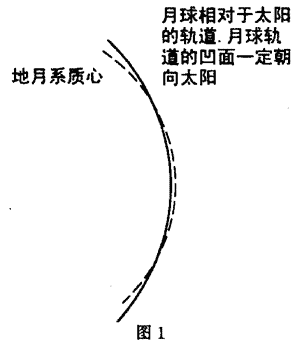实际上月球的运动一直是天体力学中的主要问题之一。详细的月球运动问题要涉及十分复杂的数学问题。常常是把月球运动理解为探索月球在地球和太阳引力作用下的运动问题，而所有三个天体都处理为质点。当我们以太阳为参考系时说月球绕地球旋转并不恰当。准确地说，月球是在绕太阳旋转。地球只是引起了月球轨道曲率的变化。从图1可见，月球轨道的凹面总是朝向太阳。这是因为作用在月球上的合力方向是向内的。甚至当月球处在地球和太阳之问亦然。

那我们在一般计算中，把月球绕地球运动看成只受地球万有引力作用，忽略太阳对月球的引力作用的处理方法和实际的情况都是相符的啊，是否真的是错了吗？原来，我们常见的处理方法是以地球为参考系来考察月球的运动的，默认地球为惯性参考系，但实际上地球并不是一个真正意义上的惯性参考系，它本身也在做绕太阳旋转的变速运动。在考察月球运动时必须考虑该变速运动带来的影响，此时可将太阳作为足够好的惯性参考系。现将月球，地球，太阳三者作为质点，考虑到地球绕太阳旋转引起的惯性力。可得方程如下。

旋转的加速度

a＝4π^2R/T²＝GM₁/R²

可得月球在此非惯性系中受惯性力为

M₃a＝M₃4π²R/T² ＝GM₁M₃/R²

由于地球到月球距离比起太阳到地球距离来说小很多，因此太阳到月球距离可认为约和太阳到地球距离相等。从上式我们可以看出此惯性力恰好和太阳对月球的吸引力相等。在地球参考系中月球受到地球吸引力，惯性力，太阳吸引力三力共同作用。惯性力和太阳吸引力两者恰好抵消，月球在地球的吸引力下围绕地球做圆周运动。实际的地球和月球系统中两者并不能简单地看成质点，因此严格来说月球是在绕两者的质心旋转。

综上所述，研究月球的运动按所选参考系的不同有两种思路。如果以太阳为参考系，那月球是在绕太阳旋转，地球只是引起了月球轨道曲率的变化，我们所见的月球绕地球旋转只是视觉上的运动。如果以地月系质心为参考系，月球是在绕地月系的质心在旋转。太阳对月球的吸引力抵消了地月系围绕太阳旋转而出现的惯性力。文中所提的一般考生的做法并没有真正理解月球的运动规律，只是将所学的公式套用下去，这也提醒了广大物理教师教学中应注意抓住物理本质，使学生真正掌握物理本质，而不是仅仅只会套公式计算。

发布时间：2009/6/26 上午8:07:06  阅读次数：10979