力学中的“自锁”现象探秘
湖北省襄樊市第一中学 蓝坤彦 选自《物理教师》2008年第12期
力学中有一类现象,当物体的某一物理量满足一定条件时,无论施以多大的力都不可能让它与另一个物体之间发生相对运动,物理上称这种现象为“自锁”。本文通过如下 3 例来进行说明。
1.通过控制角度达到“自锁”
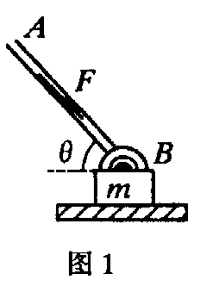 例 1:在机械设计中常用到下面的力学原理。如图 1 所示,只要使连杆 AB 与滑块 m 所在平面间的夹角 θ 大于某个值,那么,无论连杆 AB 对滑块施加多大的作用力,都不可能使之滑动,且连杆 AB 对滑块施加的作用力越大,滑块就越稳定,工程力学上称之为“自锁”现象。为使滑块能“自锁”,θ 应满足什么条件?(设滑块与所在平面问的动摩擦因数为 μ)
例 1:在机械设计中常用到下面的力学原理。如图 1 所示,只要使连杆 AB 与滑块 m 所在平面间的夹角 θ 大于某个值,那么,无论连杆 AB 对滑块施加多大的作用力,都不可能使之滑动,且连杆 AB 对滑块施加的作用力越大,滑块就越稳定,工程力学上称之为“自锁”现象。为使滑块能“自锁”,θ 应满足什么条件?(设滑块与所在平面问的动摩擦因数为 μ)
解析:滑块 m 的受力分析如图 2 所示,将力 F 分别沿水平和竖直两个方向分解,则根据平衡条件,在竖直方向上有 FN = mg + Fsinθ,在水平方向上有 Fcosθ = Ff ≤ μFN。由以上两式得 Fcosθ ≤ μmg + μFsinθ。因为力 F 可以很大,所以 μmg 可以忽略,那么上式可以变为 Fcosθ ≤ μFsinθ,则 θ 应满足的条件为 θ ≥ arccotμ。
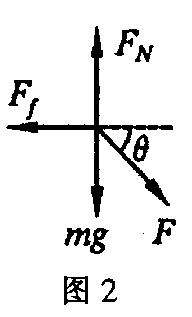
探秘:通过控制角度使推力在摩擦力方向上的分力总是小于最大静摩擦力,从而达到自锁的目的。在修建公路时,要考虑坡度就是这个道理。当坡度满足一定的条件后,即使汽车由于特殊原因在坡上熄火也能停下来,不至于下滑而无法控制。
2.通过控制摩擦因数达到“自锁”
例 2:一般家庭的门上都安装一种暗锁,这种暗锁由外壳 A、骨架 B,弹簧 C(劲度系数为 k)、锁舌 D(倾斜角 θ = 45°)、锁槽E,以及连杆、锁头等部件组成,如图 3(a)所示。
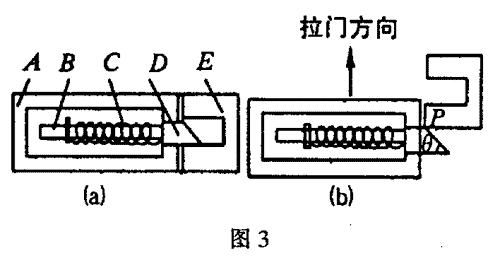
设锁舌 D 与外壳 A 和锁槽 E 之间的摩擦因数均为 μ,且受到的最大静摩擦力 f = μN(N 为正压力)。有一次放学后,当某学生准备锁门外出,他加最大力时,也不能将门关上(此种现象称为自锁),此刻暗锁所处的状态如图 3(b)所示,P 为锁舌 D 与锁槽 E 之间的接触点,弹簧由于被压缩而缩短了 x,求在正压力很大的情况下,仍然能够满足自锁条件,则 μ 至少要多大?
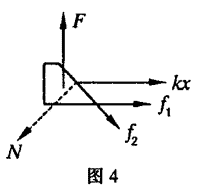
解析:受力分析如图4所示,由力的平衡条件可知
\[kx + {f_1} + {f_2}\cos 45^\circ - N\sin 45^\circ = 0\tag{1}\]
\[F - N\cos 45^\circ - {f_2}\sin 45^\circ = 0\tag{2}\]
\[{f_1} = \mu F\tag{3}\]
\[{f_2} = \mu N\tag{4}\]
由(1)~(4)式得正压力的大小
\[N = \frac{{kx}}{{(1 - {\mu ^2})\sin 45^\circ - 2\mu \cos 45^\circ }} = \frac{{\sqrt 2 kx}}{{1 - 2\mu - {\mu ^2}}}\]
当 N 趋于 ∞ 时,须有 1-2μ-μ2 = 0,解得 μ = 0.414。
探秘:摩擦因数是物体粗糙程度的反映,在其他条件相同的情况下,μ(最大静摩擦因数)越大物体受的最大静摩擦力就越大,物体越不容易被拉动。如果且达到一定程度,使其他力在摩擦力方向上的合力总是小于最大静摩擦力时,物体就达到了自锁。
3.通过控制弹力达到“自锁”
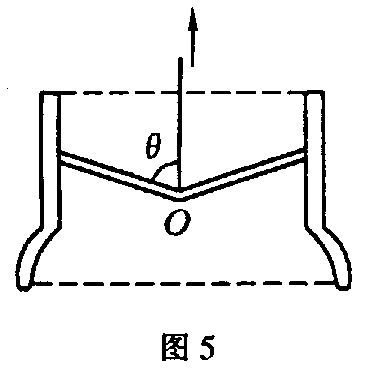
例 3:如图 5 所示,由两根短杆组成的一个自锁定起重吊钩,将它放入被吊的罐口内,使其张开一定的夹角压紧在罐壁上,当钢绳匀速向上提起时,两杆对罐壁越压越紧,若罐和短杆的承受力足够大,就能将重物提升起来,罐越重,短杆提供的压力越大,称为“自锁定机构”。若罐质量为 m,短杆与竖直方向夹角为 θ = 60°,求吊起该重物时,短杆对罐壁的压力(短杆质量不计)。
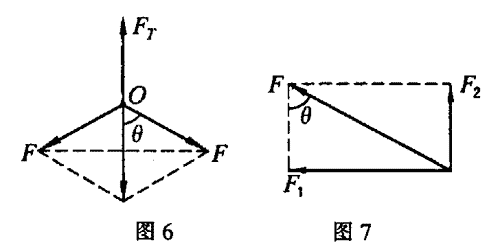
解析:对 O 点受力分析如图 6 所示,两根短杆的弹力 F(沿杆)的合力与绳子的拉力(FT = mg)等大反向,故
\[2F\cos \theta = mg\tag{1}\]
对短杆对罐壁的作用力 F 进行分解如图7所示。短杆对罐壁的压力
\[{F_1} = F\sin \theta \tag{2}\]
由(1)、(2)两式得
\[{F_1} = \frac{{\sqrt 3 }}{2}mg\]
探秘:这是一个借助巧妙的机械装置达到自锁的模型。它的原理是当自锁机构的两边与罐接触后,产生弹力和摩擦力托起罐,且罐越重,短杆提供的压力越大。这种机械装置自锁的应用在日常生活中是比较普遍的。
文件下载(已下载 3325 次)发布时间:2009/6/25 下午12:45:34 阅读次数:26848
