人造卫星的环绕速度与发射速度

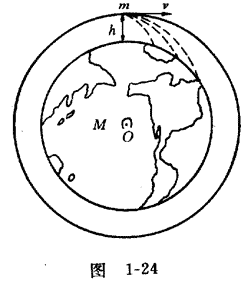我们已经知道，如果在离地面高度为 h 的地方沿水平方向发射物体，物体将受到地球引力的作用而作抛物线运动，发射的速度越大，射程也越远。如果继续增加发射速度，那么，到达某一速度的时候，物体虽然仍受到地球的引力，但不再落到地面上。这时，地球的引力起着向心力的作用，它使物体环绕地球作匀速率圆周运动。如图所示。

其实，上述环绕地球作匀速率圆周运动的物体就是一个人造卫星。下面我们首先按照匀速圆周运动所遵循的规律来找出人造卫星的环绕速度与卫星高度 h 的关系。设卫星环绕速度为 v_环，质量为 m，地球质量为 M_地，地球半径为 R₀，则根据卫星的受力情况及运动特征有：

$$\begin{array}{}\text{(1)}& G\frac{M_{地}m}{{(R_0+h)}^2}=m\frac{v_{环}^2}{R_0+h}\end{array}$$

解出：

$$\begin{array}{}\text{(2)}& v_{环}=\sqrt{\frac{G{M}_{地}}{R_0+h}}\end{array}$$

因为在地球表面处有：

$$\begin{array}{}\text{(3)}& m{g}_0=G\frac{M_{地}m}{R_0^2}\end{array}$$

式中 g₀ 是地球表面附近的重力加速度，所以 $G{M}_{地}=R_0^2{g}_0$，代入（2）式可得：

$$\begin{array}{}\text{(4)}& v_{环}=\sqrt{\frac{R_0^2{g}_0}{R_0+h}}\end{array}$$

由（4）式可知，卫星离地面越高，即 h 越大，卫星的环绕速度就越小。大概正是这个原因，有一本参考书说 ：“尽管距地面高时，环绕速度减小，但其发射速度要变大。”我们认为这本书只说对了一半。事实上，从本节开头就可知道，若卫星一开始就处在离地面高度 h 处，发射的方向又与水平平行，则此卫星的发射速度就是环绕速度。所以，在这种情况下，根据（4）式可以说，离地面越高，环绕速度越小，发射速度也越小。但是，当在地球表面发射卫星时，情况正好相反。这是因为卫星和地球作为一个系统，在不计空气阻力的情况下，不管卫星的运动状态如何，系统的机械能是守恒的。按照（4）式，卫星离地面越高，其速度或动能确实越小，但是其势能明显增大，因而系统的总机械能也要增加，相应的发射速度也要增大。具体论证如下：

若取无穷远处为万有引力势能作参考点，则万有引力势能为 ：

 $$\begin{array}{}\text{(5)}& E_{\mathrm{p}}=-\frac{G{M}_{地}m}{r}\end{array}$$

式中，r 是物体 m 距地球中心的距离。于是，地处 h 高度卫星的机械能为：

$$\begin{array}{}\text{(6)}& E_1=\frac{1}{2}m{v}_{环}^2+(-\frac{G{M}_{地}m}{R_0+h})\end{array}$$

相应地面上想把此卫星发射到预想轨道，应有的机械能为：

$$\begin{array}{}\text{(7)}& E_1=\frac{1}{2}m{v}_{发}^2+(-\frac{G{M}_{地}m}{R_0})\end{array}$$

由系统机械能守恒得：

$$E_1=E_2$$

即：

$$\frac{1}{2}m{v}_{环}^2-\frac{G{M}_{地}m}{R_0+h}=\frac{1}{2}m{v}_{发}^2-\frac{G{M}_{地}m}{R_0}$$

$$\begin{array}{}\text{(8)}& v_{发}^2=v_{环}^2+\frac{2G{M}_{地}}{R_0}+\frac{2G{M}_{地}}{R_0+h}\end{array}$$

（8）式表明，此时卫星的发射速度明显大于环绕速度。把 $v_1^2=\frac{G{M}_{地}}{R_0+h}$，$G{M}_{地}=R_0^2{g}_0$ 代入（8）式可得：

$$v_{发}^2=\frac{R_0^2{g}_0}{R_0+h}+\frac{2R_0^2{g}_0}{R_0}-\frac{R_0^2{g}_0}{R_0+h}=\frac{2R_0^2{g}_0}{R_0}-\frac{R_0^2{g}_0}{R_0+h}$$

即：

$$\begin{array}{}\text{(9)}& v_{发}=\sqrt{2R_0{g}_0\left[1-\frac{R_0}{2(R_0+h)}\right]}\end{array}$$

现在，我们从（8）、（9）两式可以清楚地看出，若在地面附近发射卫星，则卫星的环绕速度与发射速度不是同一个概念，且发射速度大于环绕速度，卫星距地面高度越高，其发射速度就越大。最后必须指出，以上讨论都是在理想情况下进行，即发射人造卫星及卫星运行过程中，我们不考虑一切阻力，卫星轨道是圆周。实际上，卫星环绕地球的运行轨道是椭圆，它的实际计算要复杂得多。

发布时间：2009/5/21 下午3:58:51  阅读次数：22759