天体质量的估算

早在80年代初，我国的物理学界就发现，在美国的研究生考题中，需要作不同程度近似处理的题目占相当比重。这类题目涉及面较广，需要考生在考场里迅速作出判断，抓住问题实质，采取有效的近似方法一针见血地加以解决。如果企图严格求解，往往劳神费时，不得要领。只有在平时学习中概念清楚、基本功扎实、善于作物理性思考的学生，才能较有把握地对付这类问题。本节我们研究如何估算太阳、地球、月亮的质量问题。

1.太阳质量的估算

我们已经测得地球绕太阳运行的平均周期为T＝3.156×10⁷秒，地球绕太阳公转半径R＝1.5×10¹¹米，于是，根据太阳对地球的引力就是地球绕太阳公转的向心力观点，可求出太阳的质量。即：

GM_日m_地/R² ＝mv_地²/R     （1）

式中G＝6.67×10^-11牛顿•米²/千克²为万有引力常数，M日为太阳的质量待求，m_地为地球质量，R＝1.5×10^-11米为太阳与地球间的平均距离，v为地球绕太阳运行的线速度。因为地球绕太阳运行的平均周期T已知，故地球绕太阳运行的线速度v可用T来表示，即：

v＝2πR/T         （2）

把（2）式代入（1）式，可得太阳质量为：

M_日＝4π²R³/GT²                   （3）

把以上G、R、T和π的数值同时代入（3）式可得： M_日≈2.00×10³⁰（千克）请读者注意，以上我们所求得的太阳质量只是一种粗略估计值，之所以是估计值，是因为：第一，实际上太阳和地球均不是一个质量均匀分布的球体；第二，地球绕太阳公转轨道并不是圆周，而是以太阳为焦点的椭圆；第三，在考察地球绕太阳的运动时，把太阳看作固定力心也有一定的近似性。实际上，研究地球绕太阳的运动是属于近似孤立两体问题，若把太阳作为固定力心，则（1）式中右边的m_地要用所谓的折合质量（或称为约化质量）：

μ＝M_日m_地/（M_日＋m_地）          （4）

代替。

2．地球质量的估算

在地球表面上的物体受到地球的引力大小是：

F＝GM_地m/R²          （1）

式中G是万有引力常数，M_地是地球质量，m是物体的质量，R是地球的半径。由于这个力物体将得到的加速度正是重力加速度g，所以根据牛顿第二定律F＝mg，我们可以得到：

GM_地/R² ＝g           （2）

式中G最早可从卡文迪许实验中测得，g可以从单摆实验中测得，R可以从地面测量中求得，于是地球的质量M地就可以从（2）式算出。现把目前公认的G＝6.67×10^－11牛顿•米²/千克²，g＝9.80米/秒²，R＝6.37×10⁶米，三个数据代入（2）式，可得：

M地＝gR²/G ≈5.97×10²⁴（千克）

必须指出，这里所求出的地球质量同样只是一种比较粗略的估计，因为地球不是一个质量均匀分布的圆球体，地球还在转动，重力加速度g的数值在地面上的不同地点也不相同。更精确地测量地球的质量还要加许多修正。

3．月球质量的估算

月球质量的估算可利用地球与月球组成的二体系统运动规律来解决。

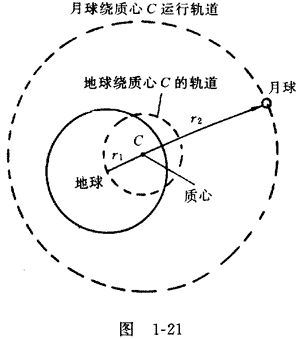
由牛顿运动定律可知，地球和月球绕它们的质心作椭圆运动，运动的周期为一个月。如图1－21所示，从观察其他行星的天空位置，可以测定地球和月球绕它们质心运动情况，并测得地心到质心的距离r₁＝4.645×10⁶米，月心到质心的距离r₂＝3.78×10⁸米。由质心定义可得：

m_地/m_月 ＝r₂/r₁          （1）

于是，可得月球的质量为：

m_月＝r₁m_地/r₂＝≈7.35×10²²（千克）

式中m地我们用了目前公认的数值，即m_地＝5.98×10²⁴千克。

发布时间：2009/5/11 上午10:10:11  阅读次数：11966