SVG 之贝塞尔曲线

使用二次和三次方程可以生成曲线。数学家在几百年前就知道这些曲线了，但是绘制它们始终是一个计算很复杂的任务。法国汽车制造商雷诺公司的工程师皮埃尔·贝塞尔（Pierre Étienne Bézier）和雪铁龙公司的物理学家和数学家保罗·德·卡斯特里奥（Paul de Casteljau）改变了这一状况，他们开发并推广了一种计算更简便的方式来生成这些曲线。

例如在 Word 中，可以通过指定两个点以及移动如图 1 中所示的“控制柄”来绘制这些贝塞尔曲线。控制柄的端点称为控制点，因为它控制着曲线的形状。当我们移动控制柄时，曲线以一种在外行看来非常神秘的方式变化着。Key Point 软件公司的图形设计师迈克·伍德（Mike Woodburn）提出了这种形象地表示控制点和曲线关系的方式：想象一下线是由柔性金属制造的。控制点内部是一个磁铁，与控制点越近，吸引力越强。

另一种形象地表示控制点作用的方法以构造曲线的 de Casteljau 算法为基础。下面的内容使用的是这种方法。

二次贝塞尔曲线

最简单的贝塞尔曲线是二次曲线。我们要指定起点、终点和控制点。想象一个搭帐篷的情景，将帐篷的两根“支柱”放在线的两个端点，这两个支柱的交点就是控制点。拉紧两个支柱中点的是一根“橡皮筋”。其中曲线弯曲的地方正好和橡皮筋的中点相连。起点/终点以及控制点之间的线是曲线的起点/终点的切线。如图2所示。

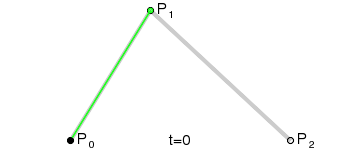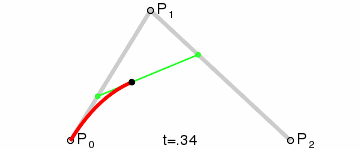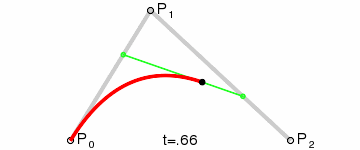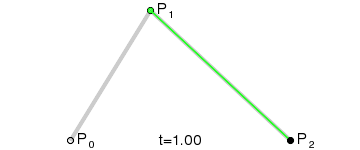
在 SVG 中生成二次贝塞尔曲线。可以通过在 <path> 数据中使用 Q 或者 q 命令指定一个二次曲线。这个命令后面紧跟着两组指定控制点和终点的坐标。大写命令意味着绝对坐标，小写命令意味着相对坐标。

下面的互动程序分别展示了显示和隐藏“支柱”的结果：

还可以在二次曲线命令后面指定多组坐标。这会生成一个多边贝塞尔曲线。假设想用 <path> 绘制一条从 (30, 100) 到 (100, 100) 并且控制点在 (80, 30) 的曲线，然后绘制一条到 (200, 80) 且控制点在 (130, 65) 的曲线。下面是这个路径的 SVG 示例，其中控制点坐标加粗了。结果如图 3 所示。

<path d="M30 100 Q 80 30, 100 100, 130 65, 200 80"/>

曲线相连接并不意味着它们在一起会很好看，SVG 还提供了流畅的二次曲线命令，用字母 T 表示（想要使用相对坐标，就用 t）。这个命令后面紧跟的是曲线的下一个端点。

控制点会自动计算，方法是“使新的控制点与上一条命令中的控制点相对于当前点中心对称”。从数学角度来讲，新的控制点 x₂, y₂ 基于上一条线段的端点 x, y 和上一个控制点 x₁, y₁，按照如下规则计算：

x₂ = x + (x − x₁) = 2 * x − x₁

y₂ = y + (y − y₁) = 2 * y − y₁

下面是一条从 (30, 100) 到 (100, 100)，控制点在 (80, 30)，然后平滑过渡到 (200, 80) 的曲线。

<path d="M30 100 Q 80 30, 100 100 T 200 80"/>

三次贝塞尔曲线

单个二次贝塞尔曲线有且只有一个顶点，或者每个曲线段都只有一个凹谷。虽然这些曲线比简单的弧线更有用，但是用三次贝塞尔曲线可以做得更好，它可以让同一个曲线图形内既有顶点也有凹谷。换句话说，三次曲线可以包含一个拐点（曲线从该点开始从一个方向往另一个方向弯曲）。

二次曲线和三次曲线之间的区别是三次曲线有两个控制点，每个端点对应一个。生成三次曲线的方式与生成二次曲线的方式类似。从图 4 中可以看到，我们绘制了三条线连接端点和控制点 a，还连接了它们的中点，生成两条线 b。然后再连接 b 的中点生成一条线 c，它的中点确定了最终曲线上的一个点。注意曲线的起点、终点和中间角度都与控制线成切线（相交）。

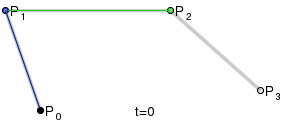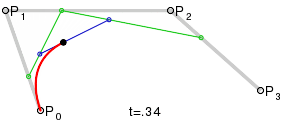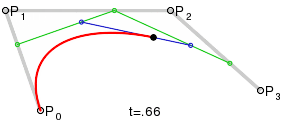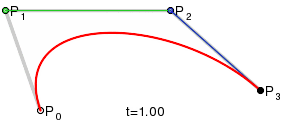
要指定一条三次曲线，使用 C 或者 c 命令。这个命令后面紧跟三组坐标，用来指定起点的控制点、终点的控制点以及端点。和其他所有路径命令一样，大写命令意味着绝对坐标，小写命令意味着相对坐标。上图中的曲线从 (20, 80) 到 (200, 120)，控制点分别在 (50, 20) 和 (150, 60)。SVG 路径如下所示：

<path d="M20 80 C 50 20, 150 60, 200 120" style="stroke: black; fill: none;"/>

和二次曲线一样，也可以通过在三次曲线命令后面指定多组坐标，来构建多条连接在一起的三次曲线。第一条曲线的最后一个点会变成下一条曲线的第一个点，以此类推。这里有一个 <path>，绘制了一条从 (30, 100) 到 (100, 100)，控制点在 (50, 50) 和 (70, 20) 的三次曲线；后面又紧跟着一条曲线，折回到 (65, 100)，控制点在 (110，130) 和 (45, 150) 处。下面是这个路径的 SVG，加粗的是控制点坐标：

<path d="M30 100 C 50 50, 70 20, 100 100,110, 130, 45, 150, 65, 100"/>

结果如图 7 所示。

如果想要保证曲线之间的连接平滑，可以使用 S 命令（或者如果想要使用相对坐标，就用 s）。在某种程度上，它和二次曲线的 T 命令类似，新的曲线会把上一条曲线的端点作为它的起点，并且它的第一个控制点是上一个终点控制点的中心对称点。我们需要提供的只是曲线的下一个端点的控制点，然后紧跟着的是下一个端点。

这里有一个三次贝塞尔曲线，从 (30,100) 到 (100,100)，控制点为 (50,30) 和 (70,50)。然后它平滑过渡到 (200,80)，使用 (150,40) 作为终点控制点，如图 8 所示。

<path d="M30 100 C 50 30, 70 50, 100 100 S 150 40, 200 80"/>

下面是互动程序，你可以拖动曲线的端点和四个控制点改变曲线的形状，也可以通过右边的复选框看看图 7 和图 8 的区别。

发布时间：2026/1/11 下午5:36:04  阅读次数：99