七、研究匀变速直线运动

在这个实验里，我们用打点计时器来研究匀变速直线运动。

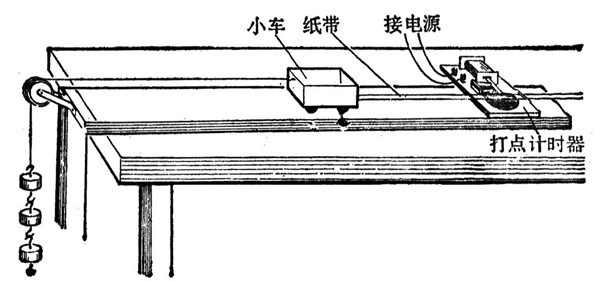
实验装置如图 10–9 所示，把附有滑轮的长木板平放在实验桌上，使滑轮伸出桌面。打点计时器固定在木板的没有滑轮的一端，把一条细绳拴在小车上，细绳跨过滑轮，下边吊着适量的钩码。穿过打点计时器的纸带固定在小车的后面，先使小车停在靠近打点计时器处，接通电源后，放开小车，让小车开始运动，随若小车的运动，打点计时器就在纸带上打下一列小点，换上新的纸带再重做两次。

下面我们来根据实验结果研究小车的运动情况，首先判断小车是否做匀变速运动。

观察纸带上的点可以发现，由于打点计时器打点很快，各点间的距离不大，特别是最初几个点比较密集，为了避免由此而产生的在测量和计算上的困难，我们可以不从第一个点开始，而在后面找一个比较方便的点开始。另外，我们还可以不用每打一次点的时间作为时间的单位，例如用每打五次点的时间作为时间的单位。这样，我们在选好的开始点下标明 0，在第六点标明 1，在第十一点标明 2⋯⋯，这些点叫做计数点。

怎样来判断小车是否做匀变速运动呢？如图 10–10 所示，我们在纸带上任意选取几个连续计数点 A，B，C，D，E……，用尺量出相邻计数点间的距离s₁，s₂，s₃，s₄，……，再算出相邻的距离之差 ∆s₁ = s₂ − s₁，∆s₂ = s₃ − s₂，∆s₃ = s₄ − s₃，……，我们知道，如果小车做匀变速运动，加速度是 a，那么，在连续相等的时间 T 内，∆s₁ = ∆s₂ = ∆s₃ = … = aT²（见第二章，练习九，第 6 题）。在这个实验里，T 就是打点计时器每打五个点所用的时间。可见，根据 ∆s₁，∆s₂，∆s₃ … 是否相等，就可以判断小车是否做匀变速运动，设计一个表格，把测出的 s₁，s₂，s₃…的数值和算出的 ∆s₁，∆s₂，∆s₃ … 的数值填入表内，可以看出各个 ∆s 在误差范围内相等，表示小车是做匀变速运动。

下面我们利用速度图象来求小车的加速度，先求出以 A 为起点，小车经过 T，2T，3T……时的即时速度 v₁，v₂，v₃……，即打点计时器打下 B，C，D……各点时的即时速度。小车是做匀变速直线运动，它在某一段时间内的平均速度等于这段时间中点时刻的即时速度（见第二章，练习九，第 5 题），所以 v₁ = \(\dfrac{{{s_1} + {s_2}}}{{2T}}\)，v₂ = \(\dfrac{{{s_2} + {s_3}}}{{2T}}\)，v₃ = \(\dfrac{{{s_3} + {s_4}}}{{2T}}\) ……打点计时器每隔 0.02 秒打一个点，所以 T = 0.02 秒×5 = 0.1 秒，再根据测得的 s₁，s₂…的数据，就可以算出 v₁，v₂，v₃……。设计一个表格，把对应的 T，v 值填入表内。用横坐标表示时间，用纵坐标表示速度，在坐标平面上画出（T，v₁），（2T，v₂），（3T，v₃）……各点。把这些点连结起来可以画出一条直线。画直线时尽量让多数的点在一直线上，不在直线上的各点，使它们对称地分布在直线的两旁。

从速度图象上求出直线的斜率，就得到小车的加速度 a。

不用速度图象来求小车的加速度，是否还有其他的方法？想出一种方法来，用这种方法根据实验数据求出小车的加速度，并跟用速度图象求出的数值相比较。

发布时间：2025/11/12 上午9:31:00  阅读次数：122