选择性必修三 第二章 气体、固体和液体 参考资料
1.物理学家
(1)玻意耳
玻意耳是英国物理学家、化学家,1627 年 1 月 25 日生于爱尔兰。他在幼年时就显示出惊人的记忆力和语言才能。他八岁在伊顿公学读书,之后在瑞士、法国、意大利学习。1654 年到牛津大学后开始从事系统的物理和化学的研究工作,积极参加了英国皇家学会的创建活动,1680 年被选为皇家学会会长。1691 年 12 月 30 日在伦敦逝世。
玻意耳曾在牛津大学建立了一个实验室,并在 1659 年利用胡克研制成的真空泵,开始对空气的性质进行研究,做了许多实验。他在助手的协助下,对一端封闭的弯管内气体体积随压强的变化做了实验研究,发现了气体体积与压强的反比关系,这是在力学运动以外的第一个自然定律。他于 1662 年发表了《关于空气的弹性与重量学说的答辩》一书,在书中介绍了他做的实验。1676 年,法国物理学家马略特也独立总结出在温度恒定时气体的压强与体积成反比的定律,他的工作虽然比玻意耳晚 14 年,但在表述上更完整。
玻意耳在物理学上的成就还有:主张热是分子的运动,首先提出色光是白光的变种,观察到静电感应现象,指出化学发光现象是冷光等。
玻意耳是近代化学的开拓者之一。他主张物质的微粒学说,提出了接近于近代的化学元素的概念,区分了化合物和混合物。玻意耳强调实验的重要意义。他研究的面很广,在流体静力学、热学、声学、医学、生物学、生理学等方面也做过许多实验,为以后实验物理学的发展作出了贡献。
(2)查理
查理是法国物理学家。他成年之后,最初在法国政府财政部当小职员。后来,他被美国物理学家富兰克林在费城雷雨中冒着生命危险研究雷电现象,勇敢探索自然界奥秘的精神所打动,对科学实验产生了浓厚的兴趣。于是,他动手制作和大量收集各种物理仪器,致力于科学实验,验证了富兰克林做过的许多实验。他举办各种物理讲座,当众出色地进行物理实验演示,在学术界赢得了很高的声誉。他经过不懈的努力,后来成为巴黎工艺学院的物理学教授,并于 1795 年被选为法国科学院院士。
查理在 1783 年首先将氢气装入气球,进行充氢气球升空实验。他随后又改进了气球的充气装置及吊起吊篮的方法,改进了测量空气流速的仪表。他与罗伯特兄弟合作,第一次实现了充氢气球升空,他和小罗伯特第一次乘这种气球上天,后来他又独自一人乘氢气球上升到三千米的高空。他们的壮举在巴黎引起了很大的轰动。
查理研究了气体的膨胀问题,发现了气体的压强随温度而改变的规律,即一定质量的气体,当体积不变时,它的压强和绝对温度成正比,这就是查理定律。他进一步发现,对于一定质量的气体,当体积不变的时候,温度每升高 1℃,压强就增加它在 0℃ 时压强的 \(\dfrac{1}{{273}}\)。查理还用它作根据,推算出气体在恒定压力下的膨胀率是个常数。这个预言后来由盖—吕萨克的实验所证实。
2.热力学系统及其平衡态
热力学是研究热现象的宏观理论。它的研究对象主要是一些由大量的微观粒子(如分子、原子等)所组成的宏观物体及物体系,这些物体或物体系叫作热力学系统,或简称为系统;而那些与系统有关的周围物体就叫作系统的外界,或简称为外界。例如,对于盛有水的开口容器来说,如果我们把水看作热力学系统的话,那么,容器及周围大气就可以认作外界。
按照热力学的规定,如果一个系统与外界既无能量的交换,又无物质的交换,这样的系统就叫孤立系统。在上面所谈的例子中,如果容器是由某些特殊材料所构成,当它封闭时可使水既不与外界交换能量,也不与外界交换物质,那么,这时的水就可以看成是一个孤立系统。不过,在自然界中,像上面所说的那种能使水与外界绝对不发生物质及能量交换的容器是不存在的。换句话说,自然界中找不到绝对孤立的系统,只是在某些条件下,当系统与外界的相互作用(或交换物质,或交换能量)小到可以忽略时,我们才可近似地把系统看成是一个孤立系统。
如果系统与外界只有能量交换,而无物质交换,这样的系统就叫作封闭系统。密闭于玻璃器皿中的水就是一个封闭系统。
如果系统与外界既有能量交换,又有物质交换这样的系统就叫开放系统。对于置于空气中的一杯水来说(假设杯子是无盖的),水就是一个开放系统。此外,地球上的所有生物,都属于典型的开放系统。
热力学系统的状态是随着系统内外条件的变化而变化的。平衡态是指系统的这样一种状态,即在没有外界(指与系统有关的周围环境)影响的条件下,系统各部分的宏观性质长时间内不发生变化的状态。这里所说的没有外界影响,是指系统与外界之间不通过做功或传热的方式交换能量,否则系统就不能达到并保持平衡态。反之就叫非平衡态。应该指出,平衡态是热力学中一个十分重要的概念,几乎所有的热力学函数都是在平衡态的情况下定义的。另外,热力学平衡与通常所说的力学平衡是有区别的。热力学平衡是指系统中大量微观粒子的平均宏观效果不随时间而改变,但从微观上看,其中的每一个粒子仍然处在一种无规则的热运动中。因此,热力学平衡是一种动态平衡。而我们知道,力学平衡则是一种相对静止的平衡。其次,系统达到热力学平衡后,仍可能出现离开这种平衡的偏差(这种现象叫涨落);而力学系统一旦达到了平衡,便会保持这种状态,而绝不出现离开这种状态的偏差。
热力学系统的平衡态是由状态参量来描述的。状态参量是一些用来表示系统固有特性的变量。依据系统特性的不同,状态参量可以分为四大类别。第一类是几何参量,它表示系统的几何特性,如体积等;第二类是力学参量,用来描述系统的力学特性,如压强等;第三类是化学参量,用来说明系统的化学特性,如组元浓度等;第四类是电磁参量,用来反映系统的电磁特性,如电场强度、磁场强度等。在具体的描述中,究竟要用几种参量以及用哪几种参量,主要以恰能完全地确定系统的状态而定。
3.温度
温度是决定一个系统是否与其他系统处于热平衡的物理量。
实验表明,如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡,那么这两个系统也一定处于热平衡。这一结论称为热力学第零定律。第零定律告诉我们,互为热平衡态的所有热力学系统具有一个数值相等的态函数,这个态函数就是温度。
温度是描述物体冷热程度的物理量。热的物体温度高,冷的物体温度低。若将两个冷热不同的物体相互接触,它们之间必然要产生热交换,最后达到热平衡,具有相同的温度。这为测量温度提供了依据。
由理想气体平均平动动能与温度的关系 \(\overline E \) = \(\dfrac{3}{{2}}\)kT,可以看出,平均平动动能 \(\overline E \) 与温度 T 成正比。也就是说,分子运动得越剧烈,温度越高。所以说,温度是组成系统大量分子无规则运动剧烈程度的标志。
要完全确定物体的温度还要确定温标,即温度的数值表示法。国际上规定的最基本的温标是热力学温标。另外,还有两种常用的温标,摄氏温标和华氏温标。
摄氏温标与热力学温标的关系为 t = T – T0,T0 = 273.15 K。式中 t 为用摄氏度温标确定的温度,T 为热力学温度。由上式可知,热力学温度的 273.15 K 为摄氏温标的零点(t = 0℃)。
华氏温标是由德国物理学家华伦海特创立的。华氏温标规定,在 101 kPa 下冰与盐水的混合物温度为 0 度,水的沸点为 212 度,中间分为 212 等分,每一等分为 1 华氏度,用符号 ℉ 表示。华氏温标与摄氏温标的关系为 F = \(\dfrac{9}{{5}}\)t + 32 ℉。
4.实际气体不能严格遵守气体实验定律的原因
玻意耳定律、查理定律和盖一吕萨克定律,都是在压强不太大(和大气压强比较)、温度不太低(和室温比较)的条件下根据实验总结出来的。当压强很大、温度很低时,由上述气体定律得出的结果就和实际测量的结果有很大的差别。为了研究方便,人们设想一种严格遵守实验定律的气体,这样的气体叫作理想气体。理想气体是不存在的,它只是实际气体在一定程度上的近似。有许多实际气体,特别是那些不易液化的气体,如氢气、氧气、氮气、空气、氦气等,在通常的温度和压强下,它们的性质很近似于理想气体的性质,可以把它们看成理想气体。这样处理的结果,误差很小,处理起来也简便多了。
那么,为什么实际气体不能严格遵守气体实验定律呢?下面就气体的等温变化来研究这一问题。下表列举了温度为 0℃ 的几种常见气体在不同压强下,压强和体积的乘积 pV 的实验值。实验所取的气体在 0℃、1.013×105 Pa 时的体积为 1 L。
| p(1.013×105 Pa) | pV(1.013×105 Pa·L) | |||
| H2 | N2 | O2 | 空气 | |
| 1 | 1.000 0 | 1.000 0 | 1.000 0 | 1.000 0 |
| 100 | 1.069 0 | 0.994 1 | 0.926 5 | 0.973 0 |
| 200 | 1.138 0 | 1.048 3 | 0.914 0 | 1.010 0 |
| 500 | 1.356 5 | 1.390 0 | 1.156 0 | 1.340 0 |
| 1 000 | 1.720 0 | 2.068 5 | 1.735 5 | 1.992 0 |
从上表可以看出,气体压强在 1.013×105 Pa 至 1.013×107 Pa 时,实验结果与玻意耳定律相差不大;压强超过 1.013×107 Pa 时,实验值与理论值之间已有显著偏离;当压强达到 1.013×108 Pa 时,玻意耳定律已完全不能适用了。
实际气体在压强很大时不能遵守玻意耳定律的原因,从分子运动论的观点来分析,有下述两个方面。
(1)分子本身占有一定的体积
分子半径的数量级为 10−10 m,若把它看成小球,每个分子的固有体积大约是 4×10−30 m3。在标准状态下,1 m3 气体中的分子数 n0 约为 3×1025 个。分子本身总的体积为 n0V = 1.2×10−4 m3,跟气体的体积比较,约为它的万分之一,可以忽略不计。
当压强较小时,由于分子本身的体积可以忽略不计,因此实际气体的性质近似于理想气体,能遵守玻意耳定律。当压强很大时,例如 p = 1×108 Pa,假定玻意耳定律仍能适用,气体的体积将缩小为原来的千分之一,分子本身的总体积约占气体体积的 \(\dfrac{1}{{10}}\)。在这种情况下,分子本身的体积就不能忽略不计了。由于气体能压缩的体积只是分子和分子之间的空隙,分子本身的体积是不能压缩的,就是说气体可以压缩的体积比它的实际体积小。由于这个原因,当压强很大时,实测实际气体的 pV 值比由玻意耳定律计算出来的理论值偏大。
(2)分子间有相互作用力
实际气体的分子间都有相互作用,除了分子相距很近表现为斥力外,相距稍远时则表现为引力,距离再大,超过几十纳米时,则相互作用力趋于 0。
当压强较小时,气体分子间距离较大,分子间相互作用力可以不计,因此实际气体的性质近似于理想气体。但当压强很大时,分子间的距离变小,分子间的相互吸引力增大。于是,靠近器壁的气体分子受到指向气体内部的引力,使分子对器壁的压力减小。因而气体对器壁的压强比不存在分子间相互作用力时的压强要小。因此,当压强很大时,实际气体的实测 pV 值比由玻意耳定律计算出来的理论值偏小。
上述两个原因中,一个是使气体的 pV 实验值偏大,另一个是使气体的 pV 实验值偏小。在这两个原因中,哪一个原因占优势,就向哪一方面发生偏离。这就是实际气体在压强很大时不能严格遵守玻意耳定律的原因。同样,把盖—吕萨克定律和查理定律用于实际气体也有偏差。
5.空间点阵
组成晶体的粒子(原子、离子或分子)在三维空间中会形成有规律的某种对称排列,如果用点来代表组成晶体的粒子,这些点的总体就称为空间点阵。点阵中的各个点,称为阵点。
空间点阵的基本特征,就是它的排列具有周期性。也就是说,从点阵中的任一阵点出发,无论向哪个方向延伸,如果经过一定距离后遇到另一个阵点,那么再经过相同的距离,必然遇到第三个阵点,如此,等等(图 2–12)。这种距离称为平移周期。在不同方向上,有不同的平移周期。取一个阵点做顶点,以不同方向上的平移周期 a、b、c 为棱长,做一个平行六面体。这样的平行六面体叫作晶胞。如果只要求反映空间点阵的周期性,就可以取体积最小的晶胞,叫作原胞。原胞的重复排列,可以形成整个点阵。
原胞的三个棱,可以选作描写点阵的基本矢量,用 a、b、c 来表示。选择任一阵点做原点,点阵中任何一个阵点的矢径都可以用方程 r = ma + nb + pc 来表示,式中的 m、n、p 都是整数。由 a、b、c 的大小和方向决定的六个参量:a、b、c、α = \(\widehat {{\boldsymbol{b}},{\boldsymbol{c}}}\),β = \(\widehat {{\boldsymbol{c}},{\boldsymbol{a}}}\),γ = \(\widehat {{\boldsymbol{a}},{\boldsymbol{b}}}\),可以确定整个点阵,所以叫作点阵常数。根据法国物理学家布喇菲的研究,晶体的构造可分为七大晶系,共有 14 种不同的点阵。
应该注意的是,空间点阵是一种数学上的抽象。理想的晶体,它的结构单元是单个原子。但是,大多数晶体的结构单元不是单个原子,而是由多个原子组成的原子群。我们把这种原子或原子群叫作基元。把基元置于阵点上就形成了晶体结构。可见,晶体结构和空间点阵,尽管有着密切的联系,仍然是两个不同的概念,不能混淆。二者之间的关系是:点阵 + 基元 = 晶体结构。图 2–13 可以说明这种关系。

6.相的概念
物质有气、液、固三种状态[1] ,人们有时也将气态、液态、固态称为气相、液相、固相。其实,相与物态不完全相同。在讨论热力学系统分类的时候,我们根据研究对象的物质组成的均匀性把热力学系统分为单相系和复相系。这表明,“相”概念的要点在于“物质性质的均匀性”。例如,通常的气态只有一个相,通常的液态也只有一个相。但能呈液晶的纯液态却有两个相(液相和液晶相)。低温下的液氦更复杂,4He 有氦 Ⅰ 和氦 Ⅱ 两个相,3He 有三个相(A 相、B 相和正常液相)。固体却可以有多个相,例如,冰有七个相(七种晶体结构),铁有四个相(在标准大气压下将铁液逐步降温,1 808 K 时结晶出体心立方 δ 铁,1 673 K时结晶出面心立方 γ 铁,1 183 K 时结晶出体心立方 β 铁,1 059 K 时结晶出有铁磁性的体心立方 α 铁),碳有三个相(金刚石、石墨和通常的无定形碳)。由此可见,在具体考察物质的性质时,相是一个十分重要的概念。严格地,在没有外界影响下,被一定边界包围的,具有确定并且均匀的物理和化学性质的一个系统或系统的一部分称为物质的一个相。由此定义和上述实例可知,相与态的差别在于:态仅考虑表观状态,而相考虑物理和化学性质的均匀性,也就是考虑物质的内部结构。
7.相平衡
系统中有几个相同时存在,而在宏观上停止相变,则系统处于相平衡。例如,水和水汽组成的体系,水和水汽之间可以互相转变,如果宏观上这种转变停止,则这个系统处于相平衡。
一个有几相存在的热力学系统,在达到热力学平衡时,必须同时达到热平衡、力学平衡和相平衡(假定未发生化学变化)。热平衡的条件是系统中各部分的温度相等,力学平衡的条件是系统中各部分的压强相等。例如,水和水汽组成的体系在达到热平衡和力学平衡时,水和水汽有共同的温度和共同的压强。热力学理论证明,要达到相平衡,两相的化学势必须相等。
由 G = U + pV – TS 定义的热力学函数叫作吉布斯函数,式中 U 为内能,p 为压强,V 为体积,T 为绝对温度,S 为熵。在处理相平衡的情况下,G 取为 T 和 p 的函数。对于单一成分的物质,1 mol 物质的吉布斯函数叫作化学势,通常以 μ 表示。
设系统中两相的共同温度为 T,共同压强为 p,第 1 相的化学势为 μ1,第 2 相的化学势为 μ2,μ1 和 μ2 是 T 和 p 的函数,可写为 μ1(T,p)和 μ2(T,p),则相平衡的条件是 μ1(T,p)= μ2(T,p)。该式说明,在两相达到平衡时,温度和压强必须满足一定的关系,这就是说,在一定压强下必须达到一定温度,才能达到相平衡。解该式可得到这个关系:p = p(T)。
对气液两相的平衡,上式表示饱和汽压与温度的关系,也就是沸点与外界压强的关系。对固液两相的平衡,上式表示熔点(凝固点)与压强的关系。对固气两相的平衡,上式表示固体上方的饱和汽压与温度的关系。
8.相图
根据相平衡条件,在两相达到平衡时,温度和压强必须满足一定的关系:p = p(T)。在 p–T 平面直角坐标系上可以作出 p = p(T)的函数图形,这种图形叫作相图,也叫作相平衡曲线。图 2–14 和图 2–15 分别给出了 H2O 和 CO2 的三相图。
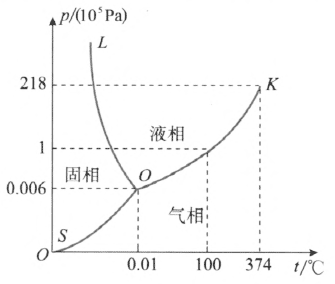
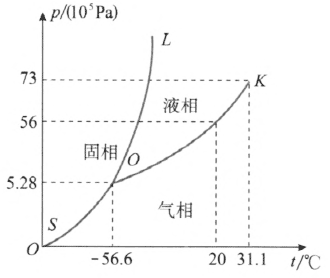
图中的 OK 是气液两相平衡曲线,它表示饱和汽压和温度的关系,亦即沸点和外界压强的关系,叫作汽化曲线。这条曲线上的各点表示气液两相平衡共存的状态。汽化曲线终止于临界点 K,温度高于临界点的温度(临界温度),不存在气液两相平衡共存的状态,只存在气相。曲线 OL 是固液两相平衡曲线,它表示熔点(凝固点)和压强的关系,叫作熔化曲线。这条曲线上的各点表示固液两相平衡共存的状态。曲线 OS 是固气两相平衡曲线,它表示固体上方饱和汽压和温度的关系,叫作升华曲线。这条曲线上的各点表示固气两相平衡共存的状态。
三条平衡曲线交于一点 O,叫作三相点。三相点对应于一个确定的温度和一个确定的压强,是固液气三相共存的唯一状态。
利用三相图可以确定在某一压强和温度下物质处于什么状态,并分析物质的相变现象。
汽化曲线和升华曲线下方为气相区域,这是因为此区域中某点所处的状态,其压强比同一温度下液气两相(或固气两相)平衡共存时的压强小,即压强小于饱和汽压,因此物质呈气相存在。在汽化曲线和熔化曲线当中的区域中,某点所处的状态,其温度比同一压强下的熔点高,但比沸点低,因此这一区域为液相区域。同样的道理可以确定另一区域为固相区域。
现以 CO2 为例分析相变现象。从 CO2 的三相图可以知道,在 1×105 Pa 下,CO2 只能以固相或气相存在;对敞开在大气中的固相 CO2 加热,固相 CO2 不经过液相而升华为气相,所以称为干冰。只有在压强高于 5.28×105 Pa的条件下,CO2 才能以液相存在,如在 20 ℃ 时,贮存在钢瓶内的液态 CO2 与其饱和汽平衡共存,压强为 56×105 Pa。如果打开钢瓶阀门,使液态 CO2 喷出,则喷出的液态 CO2 的压强由 56×105 Pa 骤然降至 1×105 Pa,在室温下 1×105 Pa 的 CO2 只能处于气态,因而喷出的 CO2 将迅速汽化。汽化过程中吸收大量汽化热,可导致另一部分 CO2 冷却而凝固成干冰,其温度可达 – 78 ℃ 左右,保存起来可作制冷剂使用。
9.表面张力
在液体表面上,任意相邻的两部分液面之间,都存在相互作用的拉力,如果在液面上想象一条分界线,则分界线两侧液面间的相互作用力,其方向与液面相切并垂直于分界线,这个力叫作表面张力。表面张力使液面具有收缩的趋势。
表面张力是由于液体表面层内分子之间的相互作用不同于液体内部而产生的。
分子间的作用力可表现为引力或斥力。分子间的作用力表现为引力的有效作用距离 s 的数量级约为 10−9 m;分子间的作用力表现为斥力的有效作用距离更短,可认为仅在分子相接触时才起作用。现以表现为引力的有效作用距离 s 作为表面层的厚度。在表面层以下液体内部某一分子 a,所受周围分子的作用力,由于对称而相互抵消(图 2–16)。在表面层内某一分子 b,所受周围液体分子的作用力并不对称,作用力的合力指向液体内部(图 2–16)。这样,在表面层内的液体分子都要受到指向液体内部的分子间作用力的作用。
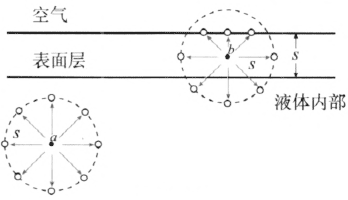
以 a 和 b 为球心,以 s 为半径,作分子作用球。以 a 为球心的球在液体内部。以 b 为球心的球,一部分在空气中;空气分子对分子 b 的作用力很小,可以忽略。
按照玻耳兹曼分布定律,表面层内分子在分子间作用力的作用下,其分子密度将发生连续变化,即越靠近液体表面,分子密度越小,分子间的距离越大。这跟地球周围大气层内分子密度随高度而减小的道理是相同的。在液体表面层里,分子间的相互作用表现为引力,这正是表面张力的来源。
10.毛细管内外液面的高度差
将毛细管插入能浸润管壁的液体,管内的液面会升高(图 2–17)。设管内的弯月面是球面的一部分,曲率半径为 R,则曲面下 A 点的压强为
\[p = {p_0} - \frac{{2\alpha }}{R}\tag*{①}\]
式中的 p0 为大气压,α 为液体的表面张力系数。这时,管内与管外水平面同高度的 B 点的压强为 p + ρgh。其中 ρ 为液体密度,h 为管内外液柱高度差,g 为重力加速度。根据流体静力学的原理,B 点的压强应与管外水平面上的压强相等,所以有
\[{p_0} = p + \rho gh\tag*{②}\]
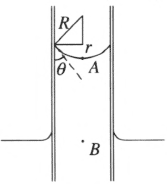
由①和②式得
\[h = \frac{{{p_0} - p}}{{\rho gr}}\tag*{③}\]
由图 2–17 可知 Rcosθ = r,式中的 r 为毛细管的内径,θ 为接触角(在液体与固体接触处,作液体表面的切线与固体表面的切线,这两条切线通过液体内部所成的角度,叫接触角)。把这个式子变形得 R = \(\dfrac{r}{{\cos \theta }}\),代入③式得
\[h = \frac{{2\alpha \cos \theta }}{{\rho gr}}\tag*{④}\]
如果将毛细管插入不浸润管壁的液体,管内液面会下降。用同样的方法可以证明,公式④对于液面下降的情况也是适用的。
11.表面张力系数
设在液面上有一分界线,长度为 l,实验表明,通过这一分界线相互作用的表面张力 F 的大小与分界线的长度 l 成正比:F = σl。式中 σ 叫作表面张力系数,数值等于液体表面单位长度分界线上的表面张力。
(1)表面张力系数 σ 与液体特性有关。密度小、容易蒸发的液体(如乙醚、酒精)的 σ 值较小,特别是液氢和液氦的 σ 值很小;不易蒸发的液体(如水银)的 σ 值较大,熔化了的金属的 σ 值很大。
(2)温度升高时,σ 值减小。
(3)σ 值与相邻物质的化学性质有关。如在 20 ℃ 时,在水与苯为界的情形下,水的 σ 值为 33.6×10−3 N/m,在与乙醚为界时为 12.2×10−3 N/m。
(4)σ 值与物质中所含杂质有关,加入杂质能显著改变液体的 σ 值,有的杂质能使 σ 值减小,有的杂质能使 σ 值增大。能使 σ 值减小的物质称为表面活性物质,肥皂就是最常见的能使水的 σ 值显著减小的表面活性物质。
12.实验注意事项
(1)表面张力实验
①肥皂液的配制:肥皂和洁净的水的体积比为 1∶150 左右,肥皂液的温度要低于或接近室温,温度高则肥皂液的表面张力就会相对减小。肥皂液的表面张力小于水,这里主要利用其黏滞性较大的特点。为增加其黏滞性可以在肥皂液中加一些食糖和几滴甘油。
②如果没有成品的表面张力实验器材,可以用直径 1 mm 左右的铁丝自制成铁丝圈,将接头处用焊锡焊上,焊点如有毛刺可用小刀刮平,这样处理后,肥皂膜不容易破。
③其他实验方法如下。
a.用塑料吸管吹出一个肥皂泡后,放开吹气口,肥皂泡自行缩小,表明液面有收缩趋势。
b.用细金属丝做成图 2–18 所示的圆环,环下焊接 3 根金属丝作支架,插入一个小玻璃瓶(装药片用的)上端的软木塞上,瓶中装适量的沙子,使整体能竖直地漂浮在水中,并只有环和支架露出水面,如图 2–18 甲所示。然后竖直向下压圆环使它浸入水中,轻轻释放后可看到圆环被水的表面层所阻挡而不能浮出水面,如图 2–18 乙所示。
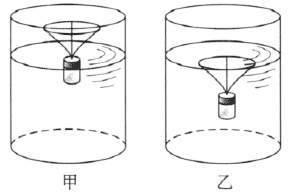
c.用水和酒精配制成与橄榄油密度相同的液体,用吸管将甲乙少许橄榄油注入这种液体中间,可看到橄榄油滴呈现球形,并悬浮。如果将苯胺注入盐水中也可看到类似的现象。
(2)毛细现象
取两块 80 mm×60 mm 的玻璃片,将它们长的一边并拢,在另一个长边间夹一根厚约 1 mm 的薄木片(火柴棍),上下两边用橡皮筋扎紧,做成一个透明楔形夹板,把它放在一只大的培养皿内。演示时,向培养皿内倒入有色水,就会看到有色水沿狭缝上升。可以看出水对容器壁浸润,和器壁接触处都向上弯曲,缝越狭窄,有色水上升得越高。这种演示器可看作由许多粗细不同的毛细管连续排列而成。可投影在屏幕上观察。
[1] 目前也常认为物质有气、液、固、等离子体、细小粉尘和玻色—爱因斯坦凝聚体六种状态。
发布时间:2025/9/18 下午3:17:57 阅读次数:1621
