选择性必修三 第一章 分子动理论 参考资料
1.扫描隧道显微镜工作原理
扫描隧道显微镜(Scanning Tunneling Microscope,STM,图 1–9)是 20 世纪 80 年代初发展起来的一种显微镜,其分辨本领是目前各种显微镜中最高的:横向分辨本领为 0.1 ~ 0.2 nm,深度分辨本领为 0.01 nm。它的高分辨本领可以清晰地展示直径大约为 10−10 m 尺度的单个原子(或分子),使人类实现了看到微小的原子的理想。

扫描隧道显微镜的工作原理与通常光学显微放大的原理截然不同。它是应用量子力学中的“隧道效应”来观察物质的原子(分子)的。
我们知道,当两个导体之间有一个绝缘体时,如果在这两个导体之间加一定的电压,一般是不会形成电流的。这是因为导体中的自由电子不能穿过绝缘体运动到另一个导体上,也就是在两个导体之间存在势垒。经典物理学认为,只有电压增大到能把绝缘层击穿,也就是势垒被击穿时,电子才会通过绝缘体。
量子力学认为,微观粒子在空间的运动是按一定的概率密度分布的。根据量子力学的计算知道,如果势垒厚度非常小,小到只有几个 10−10 m 时,电子可能穿过势垒,即从势垒的这边到达势垒的另一边,形成电流。也就是说,在势垒相当窄的情况下,电子可能在势垒上打通一条道路,穿过势垒到达势垒的另一侧,形成电流。在势垒相当窄的情况下电子能穿过势垒的现象,在量子力学中叫作隧道效应,这样形成的电流叫作隧道电流。隧道电流的强度对探测针尖与样品表面之间的距离 Z 非常敏感,这个距离每减小 1×10−10 m,隧道电流就增加一个数量级。也就是说,当探测针尖与样品靠得很近时,在探测针尖与被测样品之间就能形成隧道电流,隧道电流的大小,就反映了样品表面的原子形貌。
2.麦克斯韦速度分布
英国物理学家麦克斯韦不仅在电磁学等领域作出了杰出贡献,他在热学与统计物理学方面也作出了重要贡献。比如,麦克斯韦速度分布律就是他于 1859 年首次利用统计方法(概率观点)研究得出的。麦克斯韦速度分布描述了平衡态下不同速度的理想气体分子是如何分布的。
(1)麦克斯韦速率分布
设处于热平衡态下某气体的分子总数为 N,速率分布在 v ~ v + dv 的分子数为 dN,则速率分布在 v ~ v + dv 的分子数占总分子数的比率 \(\frac{{{\rm{d}}N}}{N}\) 应与 v 有关,并且与 dv 成正比。设 \(\frac{{{\rm{d}}N}}{N}\) 与 v 之间的函数关系为 f(v),则 \(\frac{{{\rm{d}}N}}{N}\) = f(v)dv。如果求 v1 ~ v2 的分子数 ΔN,应有 \(\frac{{\Delta N}}{N}\) = \(\int_{{v_1}}^{{v_2}} {f(v){\rm{d}}v} \)。如果对所有速率的分子求积分,即 v1 = 0,v2 = ∞,则应有 ΔN = N,\(\int_0^\infty {f(v){\rm{d}}v} \) = 1。式中 f(v)称为速率分布函数。如果确定了函数 f(v),也就确定了气体分子按速率分布的规律。
麦克斯韦用统计的方法求出了 f(v)的具体表达式,即 f(v)= \(4\pi {\left( {\frac{m}{{2\pi kT}}} \right)^{\frac{3}{2}}}{e^{ - \frac{{m{v^2}}}{{2kT}}}}{v^2}\),式中 m 为一个分子的质量,k 为玻耳兹曼常量,T 为热力学温度。
速率分布函数曲线如图 1–10 所示。它形象地描绘了气体分子按速率分布的规律。图中任意区间(v ~ v + dv)曲线下的面积,表示速率在这一区间的分子数占分子总数的比率 \(\frac{{{\rm{d}}N}}{N}\)(也可解释为,一个分子速率在 v ~ v + dv 的概率)。速率在区间 v1 ~ v2 的分子占分子总数的比率为这一区间内曲线下的面积。从图中可以看出,速率分布曲线从原点出发,随着速率的增大而逐渐升高,经过一极大值后逐渐降低,并接近横坐标轴。这说明,速率很大和很小的分子所占比率都很小,具有中等速率的分子所占比率较大。
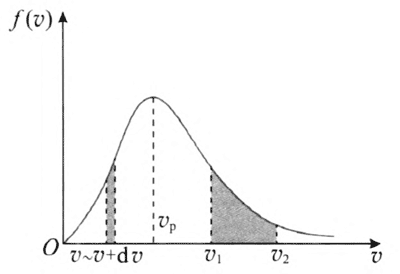
与曲线极大值相对应的速率,称为最概然速率。用 vP 表示。它的含义是,如果把整个速率范围分成许多相等的小区间,则分布在 vP 所在区间内的分子所占比率最大。vP 可根据求极值的方法,令 \(\frac{{\rm{d}}}{{{\rm{d}}v}}f(v)\) = 0,求得 vP = \(\sqrt {\frac{{2kT}}{m}} \)。可见 vP 与 T 的平方根成正比,与 m 的平方根成反比。如果 m 一定,T 增大,则气体分子运动加剧,速率小的分子数减少,速率大的分子数增多,vP 增大,曲线的极值向右移。但由于速率分布曲线下的面积恒等于 1,所以极值必然降低,曲线变得较为平坦。如果 T 一定,m 变小,则 vP 变大,曲线的极值也向右移,情形与 T 增大相仿(图 1–11)。
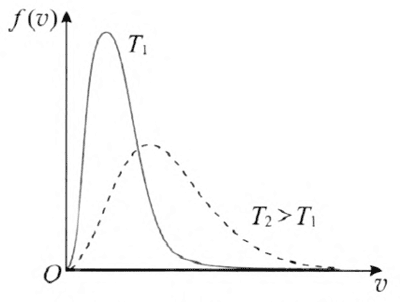
(2)麦克斯韦速度分布
如果考虑气体分子运动的方向,用 vx、vy 和 vz 分别表示气体分子速度 v 在直角坐标轴 x、y 和 z 方向上的分量,则麦克斯韦速率分布变成麦克斯韦速度分布,即 \(\frac{{{\rm{d}}N}}{N}\) = \({\left( {\frac{m}{{2\pi kT}}} \right)^{\frac{3}{2}}}{e^{ - \frac{{m(v_x^2 + v_y^2 + v_z^3)}}{{2kT}}}} \cdot {\rm{d}}{v_x}{\rm{d}}{v_y}{\rm{d}}{v_z}\),式中 \(\frac{{{\rm{d}}N}}{N}\) 为速度分量 vx 在区间 vx ~ vx + dvx,vy 在区间 vy ~ vy + dvy,vz 在区间 vz ~ vz + dvz 的分子比率。这就是同时考虑了速度的数值和方向后,分子按速度分布的规律。
3.分子动能
分子动能是指分子运动所具有的能量。组成物体的大量分子无时无刻不在做无规则的热运动,这些分子有的运动速率大,有的运动速率小,但是它们整体所表现出的宏观效果,却只与大量分子运动的平均效果有关。因而,在热现象中谈到的分子动能都是指大量分子动能的平均值(统计平均)。
如果组成物体的分子是单原子分子,则分子的运动只是平动,因而也只具有平动动能;如果分子属于双原子分子或多原子分子,则分子的运动除具有平动外,还具有转动和振动,其动能应该是平动动能、转动动能和振动动能之和。由于在高中阶段不考虑分子的振动与转动,教科书中所指的分子热运动的平均动能实际上是分子的平均平动动能。
对于理想气体,分子的平均平动动能 \(\overline E \)(\(\frac{1}{2}m\overline {{v^2}} \))与温度有如下关系:\(\overline E \) = \(\frac{3}{2}\)kT,式中 k 为玻尔兹曼常量。
大量分子的热运动是杂乱无章的,按统计的观点其平动沿 x、y、z 应该是相同的。即应有如下关系:\(\overline {v_x^2} \) = \(\overline {v_y^2} \) = \(\overline {v_z^2} \),\(\overline {{v^2}} \) = \(\overline {v_x^2} \) + \(\overline {v_y^2} \) + \(\overline {v_z^2} \),\(\frac{1}{2}m\overline {v_x^2} \) = \(\frac{1}{2}m\overline {v_y^2} \) = \(\frac{1}{2}m\overline {v_z^2} \) = \(\frac{1}{3}\)(\(\frac{1}{2}m\overline {{v^2}} \)) = \(\frac{1}{2}\)kT。x、y、z 各自对应平动的一个自由度,也就是说平均平动动能按三个自由度均分。
单原子分子只有平动,因而只有三个自由度。双原子分子除平动自由度外,还有两个转动自由度,一个振动自由度(非刚性分子)。多原子分子有三个转动自由度;如果分子是由 n 个原子组成的,则振动自由度有(3n − 6)个(n > 2)。当分子的自由度数大于 3 时,上面的结论应推广为:在温度为 T 的热平衡状态下,分子的每个自由度,平均地具有同样的动能 \(\frac{1}{2}\)kT。如果某些自由度有势能,如简谐运动的势能,则每一个这样的自由度的平均势能也是 \(\frac{1}{2}\)kT。这就是能量按自由度均分定律,简称能量均分定律。
4.分子势能
分子势能是指分子由于分子间的相互作用而具有的能量。分子间作用力属于保守力,因而可以引入势能的概念。如果两个分子间的距离改变为 dr,则势能的增量 dEp = − Fdr,即分子间势能的增量等于分子间作用力 F 在距离 dr 内所做功的负值。
若选取两个分子间相距极远(r = ∞)时的势能为 0,则距离为 r 时,分子间的势能 Ep = − \(\int_\infty ^r {F{\rm{d}}r} \)。如果采用分子间作用力半经验公式 F = \(\frac{\lambda }{{{r^s}}}\) − \(\frac{\mu }{{{r^t}}}\)(s > t),则有 Ep = − \(\int_\infty ^r {F{\rm{d}}r} \) = \(\frac{{\lambda '}}{{{r^{s - 1}}}}\) − \(\frac{{\mu '}}{{{r^{t - 1}}}}\),式中 λʹ = \(\frac{\lambda }{{s - 1}}\),μʹ = \(\frac{\mu }{{t - 1}}\)。
图 1–12 是根据上面的公式画出的势能曲线。由图可见,曲线在 r = r0 处,有一极小值,即 \({\left( {\frac{{{\rm{d}}{E_{\rm{p}}}}}{{{\rm{d}}r}}} \right)_{r = {r_0}}}\) = 0。由 F = − \({\frac{{{\rm{d}}{E_{\rm{p}}}}}{{{\rm{d}}r}}}\) 可知,在 r = r0 处 F = 0。

分子动能与温度有关,分子势能与分子间的距离有关,二者的大小决定了物质存在的状态。如果分子在平衡位置 r = r0 处的动能小于势能的绝对值,则分子只能在平衡位置附近做微小的振动。这就是物质处于凝聚态(液态或固态)时的情形。
5.内能
任何一个物体或物体系在平衡态有一个态函数 U,叫作它的内能,当这个物体系从第一个态 U1 经过一个绝热过程到第二态 U2 后,它的内能的增量等于在这过程中外界对它所做的功 W,即 U2 – U1 = W。
内能的上述定义是在焦耳实验的基础上建立起来的。焦耳用多种实验证明,在绝热过程中,为使系统状态变化所需绝热功的多少只与系统的初末两个状态有关,而与实施绝热过程的途径无关。
由于分子动理论可知,系统的内能应该等于所有分子各种形式的动能、分子内部原子间的振动势能和分子间相互作用势能总和。对于理想气体,由于不计分子间的相互作用力,也就不计分子间的相互作用势能,所以其内能只是分子的各种形式的动能和分子内原子间振动势能之和,因而只与温度有关。对于实际气体,考虑到分子间的作用力,其内能不仅与温度有关,而且与体积有关。1852 年,焦耳和威廉·汤姆孙(即开尔文)做的多孔塞实验证实了这一结论。
广义地讲,内能除包括分子动能和势能外,还应包括分子的内禀能量(如原子能量、原子核能等),但是它们在热力学研究的范围内并不发生变化,在内能的增量中可作为常量消去。
另外,内能不包括物体整体的机械能。
6.实验注意事项
(1)用油膜法估测油酸分子的大小
①用 5 ~ 10 mL 的注射器取 50 mL 的无水酒精置于烧杯中,用 0.2 mL 的有刻度的滴管(其最小刻度为 0.01 mL),吸出 0.1 mL 的酒精,烧杯中留有 49.9 mL 酒精。再用 0.2 mL 的滴管吸取油酸,将 0.1 mL 油酸滴入 49.9 mL 的酒精中,配制成 1∶500 的油酸酒精溶液。油酸酒精溶液的浓度配制准确是实验成功的关键。
滴管的胶头比较大,不容易控制吸取油酸的数量,可以取下胶头用一段 3 ~ 4 cm 长的乳胶管(乳胶管的直径与滴管相当)套在滴管上,将乳胶管另一端弯过来用线捆紧不漏气。乳胶管的弹性好,管内空气体积小,便于控制吸取油酸的数量。
②由于注射器针头不可能完全一致,各组所取 1 滴溶液的体积不一定相同。以本组实验为准。成品油膜实验仪器附带的 5 mL 注射器及针头,1 mL 大约可滴 240 滴。1 滴溶液的体积 Vʹ = \(\dfrac{{1\;{\rm{mL}}}}{{1{\rm{c}}{{\rm{m}}^3\;溶液的滴数}}}\)。1 滴溶液中含纯油酸的体积 V = Vʹ×溶液浓度。
油酸酒精溶液要现用现配,用注射器计数 1 cm3 油酸酒精溶液的滴数,滴到烧杯中的油酸酒精溶液要倒掉,不要倒回溶液瓶中,因为计数过程中,酒精要挥发,使溶液浓度发生变化。注射器中剩余的溶液可以放回溶液瓶中。保存油酸酒精溶液的瓶子用研口瓶塞,防止酒精挥发影响溶液浓度。
③在水面上撒爽身粉的方法:爽身粉装在纱布口袋内,用手捏住口袋,另一只手轻轻拍打手腕,使口袋震动,同时不断移动位置,水面上包括水面边缘都要均匀撒到。这样当油酸酒精溶液滴到水面时,油膜容易形成一个整体,不会裂成条状。如果爽身粉层的厚度较大,形成的油膜容易裂口。当油膜裂口和水盘边接上时,一部分油酸会吸附到水盘上,使油膜面积的计算发生误差,导致面积测量值不正确。这时要倒掉水盘中的水,并用洗衣粉将水盘中的油酸清洗干净,重新实验。如果不清洗水盘,则水盘边残留的油酸会影响再次测量,增加误差。
④油酸酒精溶液要滴在水面中央,滴完一滴过一段时间后油膜面积不再增大。如果油膜面积 S 太小,可以再滴一滴。因为油膜面积过小,会增加面积测量误差。油膜面积 S > 120 cm2,根据 1 mL 油酸酒精溶液的滴数,视情况滴 1 ~ 2 滴。
⑤描绘油膜边界时,眼睛的视线、笔尖与油膜边界要在同一竖直线上,以减小油膜面积的测量误差。在描绘油膜边界时注意不要震动或移动水盘,以免油膜形状发生变化,影响面积的测量。
⑥计算公式:油酸分子直径 d = \(\dfrac{V}{S}\) = \(\dfrac{{\dfrac{1}{{1{\rm{c}}{{\rm{m}}^3\;溶液的滴数}}} \times 溶液浓度}}{S}\)。
油酸分子直径数量级为 10−9 m,公认值 d = 1.12×10−9 m,实测值在 0.8×10−9 ~ 2×10−9 m 可以通过。
⑦成品油膜实验仪器的玻璃板上画有 1×1 cm2 的方格。如果没有成品仪器,可以在一张白纸上画 1×1 cm2 的方格,在玻璃板上描绘出油膜边界线后,将玻璃板放到方格纸上再数出油膜的格数,计算油膜面积。
(2)布朗运动
悬浊液的配制:用碳素墨水(不是绘图笔用的黑墨水,这种黑墨水是溶液),其中的炭颗粒较小且大小比较均匀。用 30 ~ 40 倍的清水稀释,放在试管中静置一段时间,取中间部分的悬浊液做实验。也可以用毛笔蘸一点水彩黄颜料用水稀释,使水稍呈浑浊状即可,不宜太浓。
放置悬浊液的玻璃片的制备:在玻璃片中间涂一层约 1 mm 厚的热石蜡,厚度要均匀。冷却后用小刀在石蜡中央挖出一个直径约 5 mm 的圆形槽即可。也可用橡皮泥或一定厚度的胶带围成一个槽,在槽中装满悬浊液,盖上盖玻片,里面不要有气泡。
显微镜用 600 倍或 675 倍效果较好,适当调整照射光的亮度。
用来观察布朗运动的载玻片中的悬浊液,时间长了其中的固体悬浮颗粒会沉积到玻璃片的下面,使观察效果变差。实验时玻璃片上的悬浊液现装现用。
(3)分子间的相互作用力
现在介绍一种专用仪器,它由两个空心铅柱和压紧用的支架组成(图1-13),用于演示分子间的相互作用力。

实验时,铅柱的端面用刨刀刨平。刨平端面后将两个铅柱侧面的红线对齐,如图 1–14 所示。然后将两个铅柱放到支架上,用螺旋压紧(图 1–15),再将铅柱吊挂在支架上。一般情况可以挂几千克的重物。


实验时要注意安全。铅柱挂上重物后,距桌面的距离要尽可能小一些;桌面上要有泡沫塑料或沙盘,防止重物落在桌面上;下面的铅柱要有保险绳挂在支架上,防止铅柱落下,碰伤铅柱的端面。
(4)模拟气体压强产生的机理
【实验目的】模拟气体压强产生的机理。
【实验原理】从电子秤上方不同高度处把许多粒钢珠(或绿豆)连续倒在电子秤上。用钢珠模拟气体分子;倾倒时高度越高钢珠撞击秤盘时的动能越大,可以模拟气体分子平均动能越大。把等量的钢珠在不同时间内倒完,所用时间越短,说明单位时间内撞击秤盘的钢珠越多,可以模拟单位时间内撞击器壁上的分子数越多。电子秤的示数显示钢珠对秤盘的冲击力大小,可以模拟气体压强的大小。
【实验器材】电子秤,直径 3 mm 的钢珠(或绿豆),塑料饮料瓶,薄塑料尺,塑料盆,秒表,直尺。
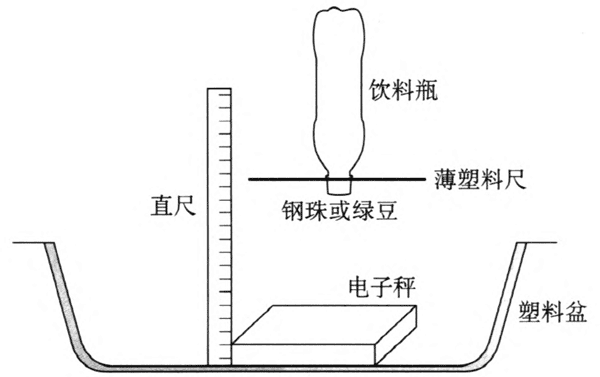
如图 1–16 所示,用钢锯在靠近瓶口的瓶颈处,平行瓶口锯开一个窄缝,缝深约为瓶颈的一半,用塑料尺插入窄缝中,控制钢珠的流量。

【实验方法】
①把电子秤放进塑料盆内,在电子秤旁竖直放置直尺,打开电子秤工作电源。
②把钢珠装入饮料瓶内,调整好薄塑料尺对瓶口的遮挡比例,用手掌堵住瓶口。
③让瓶口朝下,瓶身竖直在电子秤的正上方,使瓶口对齐直尺的某一刻度(图 1–17),放开手掌,使钢珠倒出落在电子秤上,同时用秒表记录倾倒时间,在电子秤示数比较稳定时读出示数。
④记录瓶口与电子秤之间的高度、倾倒时间、电子秤示数。
⑤改变瓶口高度,或塑料尺对瓶口的遮挡比例,重复实验。
【实验结果】
表 1 实验物品:钢珠
| 组数 | 示数稳定时瓶口的高度/cm | 倾倒时间/s | 电子秤示数/g | 瓶口遮挡情况 |
| 1 | 10 | 5.3 | 92.5 | 不遮挡 |
| 2 | 20 | 5.3 | 104.0 | 不遮挡 |
| 3 | 10 | 17.0 | 29.5 | 挡一半 |
| 4 | 20 | 17.0 | 34.0 | 挡一半 |
表 2 实验物品:绿豆
| 组数 | 示数稳定时瓶口的高度/cm | 倾倒时间/s | 电子秤示数/g | 瓶口遮挡情况 |
| 1 | 20 | 8.3 | 19.5 | 不遮挡 |
| 2 | 40 | 8.3 | 23.0 | 不遮挡 |
| 3 | 20 | 5.0 | 25.5 | 挡一半 |
| 4 | 40 | 5.0 | 35.5 | 挡一半 |
分别对比表中的 1 组和 2 组,3 组和 4 组,说明在倾倒时间相同的条件下,倾倒高度越高,钢珠对秤盘的冲击力越大,可以模拟气体温度越高时气体分子平均动能越大,气体压强越大。
分别对比表 1 或表 2 中的 1 组和 3 组,2 组和 4 组,均说明在倾倒高度相同的条件下,倾倒时间越短,钢珠对秤盘的冲击力越大,可以模拟气体分子越密集,气体压强越大。
发布时间:2025/9/16 下午9:27:00 阅读次数:785
