选择性必修二 第四章 电磁振荡与电磁波 参考资料
1.麦克斯韦对电磁理论的研究
麦克斯韦在法拉第与开尔文等人工作的启示下获得了一些研究成果,于 1855 年发表了论文《论法拉第力线》。这是他第一阶段研究工作的结晶。在这篇文章中,他用不可压缩流体的流线类比法拉第的力线,把电场、磁场与流速场类比,把电场强度、磁场强度比作流速。通过类比,他明确了两类不同的物理量,E 和 H 相当于流体力学中的力,D 和 B 相当于流体力学中的流量;流量遵从连续性方程,可以沿曲面积分,而力则可沿线段积分。通过这种类比,可以把流体力学中的数学工具移植过来,采用通量、环流、散度、旋度等具有明确定义的概念,来定量描述抽象的电场、磁场在空问的变化情况,并开始建立电磁场方程。
然而,有两个事实使麦克斯韦重新考虑他的研究方法。一个是根据伯努利流体力学,流线越密的地方压力越小,而根据法拉第力线思想,力线越密的地方应力越大,两者不宜类比。另一个是从电介质的运动来看,电的运动是平移运动,而从偏振光在晶体中的旋转现象来看,磁运动好像是介质分子的旋转运动。
由此观之,电磁现象有别于流体力学现象,电现象与磁现象也不尽相同,光靠几何上的类比无法洞察事物的本质。为了能反映电磁现象的特殊性,麦克斯韦把目光转向运用模型(电磁以太模型),并大量借助流体力学的观点和数学方法,从事艰苦的理论研究。在此基础上于 1862 年发表了《论物理力线》一文,与《论法拉第力线》相比,有了质的飞跃。不再是单纯的数学翻译,而是有了重大的引申和发展。其中意义最为重大的是提出了感应(涡旋)电场和位移电流两个全新观念,在电磁学理论研究上取得了关键性的突破。
当麦克斯韦从电磁现象的力学模型中把握住隐藏在纷繁的电磁现象背后的某些本质特征之后,他径直把电磁场作为客体,把近距作用引向深入。在实验事实和普遍动力学原理的基础上,他构建了一个全新的理论框架,全面概括电磁场的运动特征和建立电磁场方程。他于 1864 年宣读、1865 年正式发表论文《电磁场的动力学理论》。在这篇论文中,麦克斯韦提出了电磁场的普遍方程组(共二十个分量方程,包括二十个变量。若采用矢量方程,则有八个方程)。直到 1884 年,才经赫兹整理给出了简化的对称形式,整个方程组只包括四个矢量方程,一直沿用至今。
麦克斯韦由他的方程组得到了电磁波的波动方程和波在真空中的传播速度为光速 c,从而预言了电磁波的存在,并指出光是一种电磁波。
为了系统地总结电磁学的研充成果,按照一种统一的思想来总结库仑定律建立近百年来的电磁学成就和他本人十多年来取得的成果,麦克斯韦于 1873 年出版了专著《电学和磁学理论》。其中有库仑、奥斯特、安培和法拉第等人的开山之功,也有他本人的创造性研究工作,终于建立起完整的电磁场理论。其意义可与牛顿的《自然哲学的数学原理》(1687 年)和达尔文的《物种起源》(1859 年)相媲美。
电磁场理论具有如下几个特点:物理观念清新,数学结构优美,电磁时空对称,逻辑体系严密。
综上所述,麦克斯韦对电磁学的突出贡献是:
(1)提出涡旋电场和位移电流两个全新观念;
(2)用严谨的数学方程建立了完整的电磁场理论。
2.为什么电磁波在真空中也能传播
麦克斯韦在建立电磁场理论的时候,尚未摆脱机械论的影响,大量借鉴了连续介质力学的观点和方法,从而构造了“以太”这种类似弹性介质的东西。在他看来电磁波就是在“以太”中传播的弹性波。“以太”被赋予极其矛盾的机械属性,如密度极小,并无处不入.但又具有极大的切变模量等。随着近代物理的兴起,“以太”这种电磁场理论的桎梏被打破了。振荡着的电磁场本身就具有由近及远传播的功能,它不需要任何介质,在真空中就能传播,这已经是大家公认的事实。
为什么呢?原来是因为电和磁是紧密相互联系的。感应电场和位移电流从假说到被实验证实,成为麦克斯韦建立电磁场理论的重要基石,它正反映了变化的磁场产生电场和变化的电场产生磁场的客观规律。如图 4–4 所示,如果变化的磁场产生的电场也是变化着的,它又将产生磁场;如果这个磁场也是变化的,它又将产生电场。如此,变化的电磁场就可以通过相互产生而传播出去。所以,电磁波得以传播,是依赖变化的磁场产生变化的电场和变化的电场产生变化的磁场。
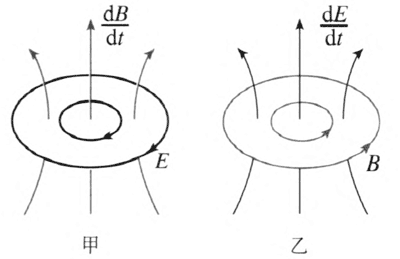
我们设想在空间某处有一个电磁振荡源,如它是一个交变的电场,它在自己周围激发磁场(图 4–5 中的实线椭圆圈),由于这个磁场也是交变的,它又在自己周围激发感应电场(图 4–5 中的虚线圆圈)。这样交变的感应电场和磁场相互激发,闭合的电场线和磁感线就像链条环节一样,一个一个地套连下去,在空间传播开,形成电磁波。图 4–5 只是电磁振荡在一个方向上传播的示意图,并非真实的电场线和磁感线的分布图。
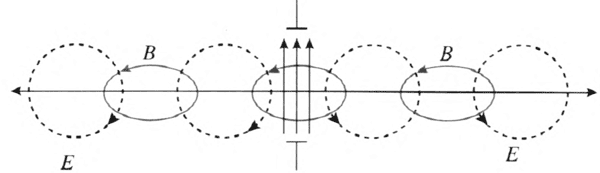
可见,电磁场性质本身决定了电磁振荡通过电与磁的相互产生而传播,形成电磁波。电磁波无须借助其他物质来传递,电磁场本身就是它的物质承担者。由真空中的麦克斯韦方程组导出的平面电磁波方程与平面机械波方程的数学结构完全相同,表明它们有相同的传播特性,电磁波传播的是 E 和 B 的变化,机械波传播的是机械振动。
重要的不同点是,真空中电磁波方程中的 ε0μ0 是一个物理常数,真空中的波速 c = \(\frac{1}{{\sqrt {{\varepsilon _0}{\mu _0}} }}\) 也是一个基本物理常数;而机械波方程中的常系数 \(\frac{\rho }{E}\) 和波速 v = \(\sqrt {\frac{E}{\rho }} \) 由介质的力学性质决定,机械波的传播必须借助于弹性介质。
3.介质对电磁波的影响
电磁波是依赖变化的电场和磁场相互产生这种机制传播而不需要借助于介质。但是,由于电场和磁场与物质间存在相互作用,介质对在其中传播的电磁波也是有影响的。这种影响又依介质的物理性质不同而异。下面扼要介绍不同介质对平面电磁波的影响。
(1)在无损耗的非色散电介质中,电磁波的传播速度即相位传播速度(相速)与电磁波的频率无关,依赖介质的相对介电常数和相对磁导率,总是小于真空中的光速,即
\[v = \frac{c}{{\sqrt {{\varepsilon _{\rm{r}}}{\mu _{\rm{r}}}} }}\]
(2)在无损耗的色散电介质中,电磁波的相速度依赖频率(或波长)。由于色散介质的分子在电场中的极化与电场的频率有关,因而介电常数区别于通常的静态介电常数,它依赖电场变化的频率。所以电磁波的相速度与频率(或波长)有关。
色散介质又分为正常色散介质和反常色散介质两类。在正常色散介质中,电磁波的相速度随波长增长而增大,\(\frac{{{\rm{d}}v}}{{{\rm{d}}\lambda }}\) > 0;在反常色散介质中,相速度随波长增长而减小,\(\frac{{{\rm{d}}v}}{{{\rm{d}}\lambda }}\) < 0。
色散介质中电磁波的相速度依赖频率变化的例子,人们熟知的是光(电磁波)通过三棱镜后的色散现象。由于相速度与频率有关,因而三棱镜对光的折射率 n = \(\frac{c}{v}\)(≈ \(\sqrt {{\varepsilon _{\rm{r}}}} \))与入射光频率有关。正常色散介质如玻璃、水晶等,它们的折射率 n 随波长增大而减小。因此,包括各种可见光频率的复色光(白光)通过三棱镜后,不同频率的单色光因折射率不同而有不同的折射角。紫光波长最短因而折射率最大,偏折角最大;红光波长最长,折射率最小,因而偏折角最小。于是白光通过三棱镜折射以后,发生色散,形成了彩色连续光谱。
(3)导体的电导率不为 0(σ ≠ 0),在导体内的电磁振荡中,变化电场要形成传导电流,这将不可逆地把电磁场的能量转换为内能。因此.导体将损耗(或吸收)电磁波的能量,使进入导体的电磁波很快地衰减为 0。电磁波不能透过导体而传播。
频率越高的电磁波渗入导体的深度越浅,低频电磁波的渗透深度较大。所以,薄层的导电材料可以透过低频的电磁波,对电磁波能起到低通滤波器的作用。
4.电磁波的产生与传播中的相位问题
对于电磁波的产生与传播,经常有两个疑问:电磁波在产生之初电场与磁场具有相位差,为何在传播的过程中慢慢变得相位相同了呢?如果说变化的磁场产生电场,那么磁场变化晟快的时候电场应该最大,磁场最大时变化得最慢,电场应该最小,所以电场和磁场的相位不可能相同。电磁波在传播中电场与磁场相位相同,它的机制是什么?
电磁场运动的机制就是用麦克斯韦方程组对它进行解释,由于中学物理没有涉及麦克斯韦方程组,所以讨论起来有不小的困难。
图 4–6 所示为一根长度为 l 的绝缘细杆,两端各有一个点电荷,两个点电荷的电荷量(+ q 和 − q)等值异号,这个带电体叫作电偶极子。描述电偶极子的物理量叫电偶极矩 p,p = lq,电偶极矩是矢量,方向由负点电荷指向正点电荷。


发射电磁振荡的天线中的一小段叫一个天线基元。天线基元可以想象为由一根长为 l 的导电金属细棒和两端的两个金属小球构成。图 4–7 中金属细棒内流有高频交变电流 i(t),两个金属小球依然带有等值异号电荷,但电荷量和带电的正负都随高频电流 i(t)而高速变化。比较图 4–6 和图 4–7,可见天线基元也就是一个电偶极子,电偶极矩依然是 p = lq,只是 q 高速变化,而且金属细棒内有高频交变电流 i(t)通过而已,一般把这样的天线基元称为偶极振子。设交变电流 i(t)随时间按简谐规律变化
\[i(t) = {I_{\rm{m}}}\sin \omega t\;\;({I_{\rm{m}}}\;为振幅)\tag{1}\]
则小球带电
\[{q_{上球}}(t) = - \frac{{{I_{\rm{m}}}}}{\omega }\cos \omega t,{q_{下球}}(t) = \frac{{{I_{\rm{m}}}}}{\omega }\cos \omega t\tag{2}\]
由于偶极振子的电磁振荡会向四面八方传播,建立如图 4–8 中 Oxyz 的三维直角坐标系,O 位于偶极振子 l 的中点,z 沿偶极振子 p 的方向,研究 x 轴上各点由偶极振子产生的电磁场。

通过求解电磁学的基本动力学方程——以偶极振子的电流和电荷为场源的麦克斯韦方程组,就可以求出偶极振子 p 在空间产生的电磁场。引入 k = \(\frac{\omega }{c}\)(c 为光速)。在 x 轴上与原点距离为 r 的 P 点处
\[{E_x} = {E_y} = 0,{B_x} = {B_z} = 0\]
\[{E_z} = - \frac{{l{I_{\rm{m}}}}}{{4\pi {\varepsilon _0}\omega }}{k^3}\left[ {\frac{1}{{kr}}\cos \omega \left( {t - \frac{r}{c}} \right) + \frac{1}{{{{(kr)}^2}}}\sin \omega \left( {t - \frac{r}{c}} \right) - \frac{1}{{{{(kr)}^2}}}\cos \omega \left( {t - \frac{r}{c}} \right)} \right]\tag{3}\]
\[{B_y} = \frac{{{\mu _0}l{I_{\rm{m}}}}}{{4\pi }}{k^2}\left[ {\frac{1}{{kr}}\cos \omega \left( {t - \frac{r}{c}} \right) + \frac{1}{{{{(kr)}^2}}}\sin \omega \left( {t - \frac{r}{c}} \right)} \right]\tag{4}\]
首先,将①②式与③④式比较,可以发现:电场、磁场与电荷、电流的变化规律不完全相同,电荷、电流的相位是 \(\frac{\omega }{t}\),而电场、磁场的相位是 \(\frac{\omega }{{t - \frac{r}{c}}}\)。是电磁振荡由原点传到 P 点的时间,这个差别正是说明了 t 时刻的电磁场由 t − \(\frac{r}{c}\) 时刻的电荷、电流决定,反映了电磁振荡以光速 c 由原点传到 P 点的传播特征,物理学中把这个效应叫作推迟效应。此外 sin 和 cos 函数形式的差别,则是说明它们之间可能存在 \(\frac{\pi }{2}\) 的相位差。
由于③④式比较复杂,我们讨论两个极端的情况。
(1)kr ≫ 1 的远区
因为 kr ≫ 1,所以 \(\frac{1}{{kr}}\) ≫ \(\frac{1}{{{{(kr)}^2}}}\) ≫ \(\frac{1}{{{{(kr)}^3}}}\),于是近似有
\[E = {E_z} = - \frac{{l{I_{\rm{m}}}}}{{4\pi {\varepsilon _0}\omega }}{k^2}\frac{1}{r}\cos \omega \left( {t - \frac{r}{c}} \right)\]
\[B = {B_y} = \frac{{{\mu _0}l{I_{\rm{m}}}}}{{4\pi }}k\frac{1}{r}\cos \omega \left( {t - \frac{r}{c}} \right)\]
可见偶极振子远区的电场 E 和磁场 B 是同频率同相位的简谐波。E 和 B 的同频率同相位,保证了能量只能由近而远地单向传播。另外由于 E 和 B 均反比于 r,故 EB 反比于 r2。因为 E 和 B 的乘积 EB 决定了能量传输的强弱,而以 O 为球心的球面面积正比于 r2,所以偶极振子远区的电磁场能使能量源源不断地向外传播,而且通过不同半径 r 的球面的能量为一个常量。这种有能量不间断、单方向地流到无穷远去的电磁场称为辐射电磁场,辐射电磁场就是平时说的电磁波。
(2)kr ≪ 1 的近区
因为 kr ≪ 1,所以 \(\frac{1}{{kr}}\) ≪ \(\frac{1}{{{{(kr)}^2}}}\) ≪ \(\frac{1}{{{{(kr)}^3}}}\),于是近似有
\[E = {E_z} = \frac{{l{I_{\rm{m}}}}}{{4\pi {\varepsilon _0}\omega {r^3}}}\cos \omega t = - \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{l{q_{上球}}(t)}}{{{r^3}}}\tag{5}\]
\[B = {B_y} = \frac{{{\mu _0}l{I_{\rm{m}}}}}{{4\pi }}\sin \omega t = \frac{{{\mu _0}}}{{4\pi }} \cdot \frac{{li(t)}}{{{r^2}}}\tag{6}\]
⑤⑥式就是借助静电场和静磁场的公式计算所得的结果,只是 q上球(t)和 i(t)随时间变化而已。因此⑤⑥式中推迟效应不见了。这种忽略推迟效应的近似称为似稳近似,在这种近似下讨论的电磁场和电路称为似稳电磁场和似稳电路。中学物理课程中涉及的通常都是似稳电磁场和似稳电路。
由⑤⑥式可以看出:偶极振子近区的电场 E 和磁场 B 不再具有波动形式,而是具有简谐振动的形式。电场 E 和磁场 B 的振动分别用函数 cosωt 和 sinωt 描写,所以二者之间具有 \(\frac{\pi }{2}\) 的相位差,具有这样相位差的电磁场,平均而言没有由近而远的能量流动。
所以,偶极振子近区的电磁场不是辐射场,或者说不是电磁波。因此,电磁波在产生之初电场与磁场具有相位差的说法不太妥当,因为产生之初还不是电磁波。
再回过头去看看③④式,可见:③④式中的第一项描述了辐射场,其他项不是辐射场。只有在远区第一项才占主导地位,所以电磁波仅存在于远区。③④式既包含远区成分(第一项),也包括近区成分(最后一项)。在近区,第一项的远区成分实际上依然存在,它是远区向外传播的能量的来源,只是它被近区成分所掩盖,不能被观测而已。在远区,近区成分也依然存在,但它已经衰减得不能被观测了。在近区和远区之间,存在过渡区,过渡区内情况很复杂,不太好研究。
5.太阳辐射
太阳辐射的波长范围涵盖了 γ 射线、X 射线、紫外线、可见光、红外线和射电等不同波段。太阳辐射的主要能量集中在可见光波段和近红外波段,波长 200 ~ 1 000 nm 的辐射能占了太阳总辐射能的 99.9%。波长在 550 nm 的黄绿光附近,辐射的能量最强。太阳辐射强度范围变化极大,从最强的可见光区到最弱的射电米波区强度变化达到 26 个量级。将太阳辐射能谱分布曲线与黑体辐射比较,可以估算出太阳温度约为 6 000 K。
太阳辐射能谱呈现出复杂的结构,是由于不同波段的太阳辐射实际上来自太阳大气的不同层。太阳大气由三层组成,最下面是光球层,也就是我们通常肉眼能看到的光亮日面,光球层很薄,厚度只有约 500 km,形成非常清晰的边界,但大部分日光是由光球发出的。光球之上是色球层,色球厚度较厚,平均厚度约 2 500 km,但外缘参差不齐。色球密度比光球低,而温度比光球更高。日全食时,黑色月轮边缘呈现的粉红色区域就是色球。从太阳色球图上常常可以看见明亮的太阳谱斑、细长的暗条和伸出太阳边缘的日珥。色球层之上都称为日冕,日冕大气更加稀薄,但温度却可以高达百万摄氏度。日全食时,太阳周围的银白色光晕就是日冕。日冕是不均匀的,包含有许多不同结构,并随着时间不断变化。日冕的范围从太阳附近一直延伸到更深远的地方。实际上,广义上的日冕直接延伸到太阳系边缘。
太阳大气的这些层各有特性,它们发射的辐射也具有不同的光谱特征。光球层中,光球下层温度较高,产生的辐射较强,在向外辐射的过程中,某些波长的光会被光球大气中的各种中性或电离的原子或分子吸收,于是从光球表面射出的主要是上层较弱的辐射,因此在这些波长处的辐射强度显得比邻近波长的辐射弱,呈现为吸收线。太阳光谱中,200 ~ 1 000 nm(可见光和近红外)波段叠加在连续光谱上的 2 万多条吸收线就是这样形成的。色球和日冕温度较高,其中的各种中性和电离原子发生跃迁时会发出对应波长的谱线,其强度高于背景的连续谱.形成了明亮的发射线。因此.在太阳光谱的小于 150 nm(紫外和 X 射线)波段,发射线明显,连续谱则较弱。在中间的过渡谱段,则会出现吸收线和发射线并存的情形。由于光球的不透明度在红外区随波长增大而增大,因此在 1 000 nm ~ 1 mm(红外区)的谱段,太阳光谱主要是光球上层大气贡献的,其发射谱线比背景连续谱强则呈现为发射线,比背景弱则呈现为吸收线。大于 1 mm 的射电谱段,主要是色球和日冕贡献的连续谱。
太阳辐射虽然涵盖多个波段,但是由于地球大气的吸收,能够到达地面的只有可见光区和红外区的一些透明窗口,以及射电波段,而紫外线、X 射线和 γ 射线都只能在高空甚至太空进行测量。随着卫星技术的发展.太阳观测已经从地面扩展到太空,利用卫星搭载的太阳望远镜,可以观测到太阳各个波段的面貌。
例如,太阳动力学观测台(SDO卫星)于 2010 年 2 月发射升空,多年来以高时间分辨率、高成像分辨率拍摄了海量的太阳图像,积累了丰富的太阳监测资料。SDO 卫星拍摄太阳日冕的仪器被称为大气成像组件,可以提供多谱段、近实时、宽覆盖的高分辨率日冕图像,其成像谱段多达 9 个,位于极紫外区,对应太阳光谱中的明亮发射线。不同谱段拍摄的太阳图像形态各异,与肉眼看到的太阳也大相径庭。教材中就提供了波长为 21.1 nm 的谱段拍摄的太阳图像,通过上网搜索“SDO”可以随时看到这些图像。
此外,太阳爆发活动也会导致太阳辐射的变化。例如,当太阳上爆发耀斑时,日面上发生耀斑的区域会发射出增强的电磁辐射和高能粒子流,特别是在 X 射线、紫外波段和射电波段附加辐射非常强,可以高出背景值几个量级。
6.通信公司如何区分手机是关机还是不在服务区
手机一旦开机就会发出信号,基站收到这个信号后即可确定手机处于开机状态并确定手机在哪个基站附近。手机在开机状态下会间歇地与基站联系,通信公司可以通过基站对手机定位,当有人呼叫这部手机时就可以立即联系到这部手机。
如果处于开机状态的手机接收不到基站的信号就会频繁地发出信号寻求联系。手机在待机状态下,不但手机内部电路要消耗电能,还会因辐射(发出信号)消耗电能,因此在没有信号的地方打开手机会使手机待机耗电量大增。
手机关机时也会发出信号,基站收到信号后即可确定手机处于关机状态,再有人呼叫这部手机时,通信公司就会以手机关机来答复。如果基站收到过手机开机信号而没有再收到关机信号,而当有人呼叫这部手机时基站和手机又失去了联系,通信公司就会以手机不在服务区答复。
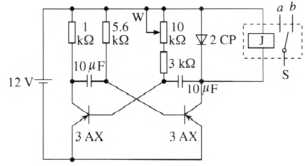
7.电磁振荡的产生
教材图 4.1–2 所示的振荡电路中能产生阻尼振荡的必要条件是电路中的电阻 R < 2\(\sqrt {\frac{L}{C}} \),所以应采用粗导线在铁芯上绕制自感系数相当大的线圈,电容却不可过大。
用指针式电表显示振荡电流时,为便于观测,振荡的周期应不小于 0.5 s,且振荡持续的时间要长些,使其能观察到 3 ~ 5 个周期。为此应使线圈的自感系数尽量大些,电容也适当大些,线圈和电表的电阻要尽量小。所用电流表的指针动圈游丝系统的惯性应尽量小,才能使指针的运动和振荡电流的变化接近同步。为了避免在振荡电流消失后,指针系统由于自身惯性仍来回振动造成假象,应当给电表并联一个阻值适当的阻尼电阻,当电流消失后指针能直接回到平衡位置。
J 2434 型电磁振荡演示仪能达到上述要求。它所附的阻尼振荡示教板电路如图 4–9 所示,L 为特制的有抽头大电感线圈,接 1 ~ 4 时电感大于 500 H,电阻小于 50 Ω,C 为 200 μF 金属化纸介电容器,A 为仪器所附的灵敏电流表,内部接有阻值适当的阻尼电阻,表盘刻度零点左右各 30 格。实验时开关 S 先接 a 再扳向 b,可看到表针同零点左右摆动,周期约 2 s,振幅逐渐衰减,振荡 5 个周期后振幅衰减到 1 格以下。如 C 用电解电容器,反向漏电较严重,加快了能量损耗,振荡持续的时间将变短。
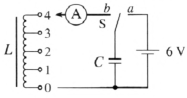
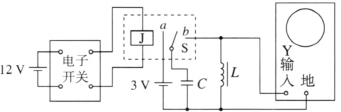
用示波器代替指针式电表能直接显示振荡的图像,并且因为示波管中电子的惯性极小,可以显示高频率的振荡电流,从而避免使用大电感演示。实验电路如图 4–10 所示,L 为 J2425 型变压器原理说明器的 400 匝线圈或 J2423 型可拆变压器的 800 匝线圈,套在闭合铁芯上,电感仅几亨,C 为 2μF 电容器。虚线框内为 J2466 型无线电组合教具中的电磁继电器,J 是它内部电磁铁线圈,用继电器的接点来控制 C 的充、放电。“电子开关”是无线电组合教具中的一个组件,是一个晶体管自激多谐振荡器,有的产品中无此组件,可用有关零件按图 4–11 所示电路组成。接通 12 V 电源,电子开关工作,线圈 J 中通过矩形脉冲电流,使继电器的动接点 S 按一定频率在静接点 a、b 间反复转换。J2458 型教学示波器的输入耦合开关置于“DC”,Y 轴衰减置于“×100”挡,X 轴扫描频率10 ~ 100 Hz,仔细调节扫描微调旋钮,使扫描频率恰好等于继电器动接点转换频率时,就可看到稳定的阻尼振荡的电压–时间图像。再调 Y 增益和 X 增益使图像有适当的幅度和横向展开。为使图像有典型性,应显示出 3 ~ 5 个周期的波形,所以要适当搭配 L、C 值,使电磁振荡的频率是继电器转换频率的 6 ~ 8 倍。对于图 4–11,可以调节电位器 W 改变电子开关所产生的矩形脉冲频率从而改变继电器转换的频率。
8.电磁波的发射和接收
(1)将两个球形导体装在两根拉杆天线粗端,再将拉杆天线固定在感应圉上,使两个球形导体相距约 5 mm(图 4–12 甲),作为发射天线。
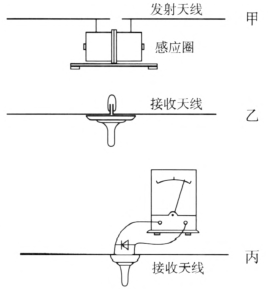
(2)将氖泡和另外两根拉杆天线装在绝缘手柄上,并将氖泡的两端分别接于拉杆天线的粗端(图 4–12 乙),作为接收天线。
(3)接通感应圈的电源,使感应圈工作。这时必须先安好天线,再接通电源。
(4)将接收天线的长度调节成与发射天线的长度相同。将接收天线平行地逐步靠近发射天线,可看到氖泡逐渐发光。说明发射天线发射出电磁波,接收天线收到电磁波,并且产生了电谐振,谐振电流使氖泡发光。
(5)改变接收天线的长度,或转过一定的角度,可看到氖泡变暗或熄灭。说明接收天线与电磁波不产生电谐振时,接收到的电磁波的能量很小。
(6)取下接收器的氖泡,在两根拉杆天线的邻近端接上一只晶体二极管(2 AP 型),然后再与电流表并联(图 4–12 丙)。重复上述过程,当接收器收到电磁波时,电流表的指针就发生偏转,接收距离可达几米。
发布时间:2025/9/12 下午1:14:09 阅读次数:575
