选择性必修二 第三章 交变电流 参考资料

1．正弦交变电流的有效值

交变电流的瞬时值 i 随时间变化 i = i（t）。如果交变电流流经一个阻值不变的电阻 R，在一个周期内消耗的能量跟某一恒定电流经过同一电阻在同一时间内消耗的能量相等，则此恒定电流 I 的大小就是交变电流 i 的有效值。它们之间的关系是

\[{I^2}RT = \int_0^T {R{i^2}(t){\rm{d}}t} \]

即交变电流的有效值

\[I = \sqrt {\frac{1}{T}\int_0^T {{i^2}(t){\rm{d}}t} } \]

交流电压 u = u（t），其有效值

\[U = \sqrt {\frac{1}{T}\int_0^T {{u^2}(t){\rm{d}}t} } \]

在电阻 R 上消耗的瞬时功率 p（t）= i（t）u（t）。通常有实际意义的不是瞬时功率，而是平均功率。平均功率是瞬时功率在一个周期 T 内对时间的平均值

\[\overline P  = \frac{1}{T}\int_0^T {p(t){\rm{d}}t}  = \frac{1}{T}\int_0^T {i(t)u(t){\rm{d}}t} \]

对于正弦式交变电流

\[i(t) = {I_{\rm{m}}}\sin \omega t\]

在纯电阻电路中，i（t）与 u（t）同相，无相位差，所以

\[u(t) = {U_{\rm{m}}}\sin \omega t\]

在一个周期 T 内的平均功率为

\[\begin{array}{l}\overline P  = \frac{1}{T}\int_0^T {p(t){\rm{d}}t} \\ = \frac{1}{T}\int_0^T {i(t)u(t){\rm{d}}t} \\ = \frac{1}{T}\int_0^T {{I_{\rm{m}}}{U_{\rm{m}}}{{\sin }^2}\omega t{\rm{d}}t} \\ = \frac{1}{2}{I_{\rm{m}}}{U_{\rm{m}}}\\ = \frac{1}{2}I_{\rm{m}}^2R\end{array}\]

在纯电阻电路中，u（t）、i（t）和 p（t）随时间的变化曲线如图 3–8 所示，由于 u（t）、i（t）相位一致，因而任何时刻输入元件中的瞬时功率 p（t）都是正的，这些能量全部转化为焦耳热，这跟恒定电流是一样的。

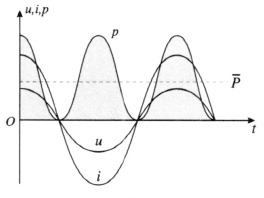
对于恒定电流 I 来说，

\[P = UI = {I^2}R\]

比较（1）式和（2）式可知

\[I = \frac{{{I_{\rm{m}}}}}{{\sqrt 2 }}\]

同理可得

\[U = \frac{{{U_{\rm{m}}}}}{{\sqrt 2 }}\]

以上便是正弦式交变电流的电流有效值、电压有效值跟峰值间的关系。

2．正弦交变电流流整流后的有效值和平均值

正弦式交变电流经全波整流后，其波形图如图 3–9 甲所示；瞬时电流的二次方 i²（t）的图像如图 3–9 乙所示。全波整流后，电流的方均根值应与整流前相同，故 I = \(\frac{{{I_{\rm{m}}}}}{{\sqrt 2 }}\) 仍然适用。

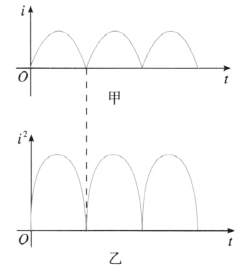
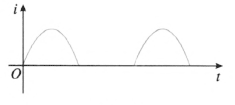
但经半波整流后，波形图如图 3–10 所示。由于每一个周期内，都有半个周期电流为 0。故一个周期内电流的有效值

\[I = \sqrt {\frac{1}{T}\left[ {\int_0^{\frac{T}{2}} {I_{\rm{m}}^2{{\sin }^2}\left( {\frac{{2\pi }}{T}t} \right){\rm{d}}t + \int_{\frac{T}{2}}^T {0{\rm{d}}t} } } \right]} \]

\[ = {I_{\rm{m}}}\sqrt {\frac{1}{{2T}}{{\left[ {t - \frac{{\sin \left( {2 \times \frac{{2\pi }}{T}t} \right)}}{{2 \times \frac{{2\pi }}{T}}}} \right]}^{\frac{T}{2}}}} \]

\[ = \frac{{{I_{\rm{m}}}}}{2}???\]

可见，半波整流后的有效值为整流前的 \(\frac{1}{{\sqrt 2 }}\)。

3．什么是理想变压器？

对于理想变压器，主要有两种观点。一种观点认为，理想变压器是没有能量损耗（铜损和铁损）的变压器，并认为在这种条件下，变压比公式 \(\frac{{{U_1}}}{{{U_2}}}\) = \(\frac{{{n_1}}}{{{n_2}}}\) 和变流比公式 \(\frac{{{I_1}}}{{{I_2}}}\) = \(\frac{{{n_2}}}{{{n_1}}}\) 严格成立；另一种观点认为，除没有铜损和铁损外，还应加上没有漏磁的条件，才是理想变压器，并认为，即使在这样的条件下，变流比公式也不严格成立。

下面我们从变压比公式的成立条件等方面讨论这个问题。

设变压器空载时，原线圈加有电压 U₁，通过原线圈的空载电流（励磁电流）为 I₀，并假定（理想化条件）：

①变压器没有铜损（即不计电阻引起的热损耗）和铁损（即铁芯中无磁滞和涡流损耗），变压器作为纯电感接入电路；

②电流 I₀ 只在铁芯中建立磁通量，即变压器铁芯没有漏磁通量，原、副线圈内磁通量完全相等，如图 3–11 所示。

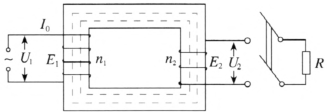
对于简谐交变电压 u₁ =U_1mcosωt = U_1msin（ωt + \(\frac{\pi }{2}\)），因为原、副线圈是纯电感性的，所以有效值 \(\frac{{{U_1}}}{{{U_2}}}\) = \(\frac{{{n_1}}}{{{n_2}}}\)。这就是说，在没有漏磁和铜损、铁损的条件下，变压比公式准确成立。这个结论与负载是否接入无关。

如果铁芯有漏磁通量 Φ_p（为简化讨论，设漏磁通量仅存在于原线圈一侧），如图 3–12。则穿过副线圈的磁通量 Φ₂ 仅是电流 I₀ 激起的磁通量 Φ₁ 的一部分（一般情况是很大一部分）。通常把 Φ₂ = Φ₁ = Φ 称主磁通量或工作磁通量。漏磁通量不穿过副线圈，但在原线圈中产生与 u₁ 同相的感生电动势。

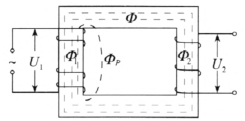
原、副线圈的电压比 \(\frac{{{U_1}}}{{{U_2}}}\) = \(\frac{{{n_1}\omega ({\Phi _{\rm{m}}} + {\Phi _{{\rm{pm}}}})}}{{{n_2}\omega {\Phi _{\rm{m}}}}}\) ≠ \(\frac{{{n_1}}}{{{n_2}}}\)。这就是说，在有漏磁通量的情况下，即使没有铜损和铁损，变压比公式也不再严格成立。

在空载情况下，只要变压器是纯电感性的，则电压 u₁ 的相位超前于电流 i₀ 的相位 \(\frac{\pi }{2}\)，电动势 e₂ 的相位落后于 i₀ 的相位 \(\frac{\pi }{2}\)，故 u₁ 与 e₁ 的相位差为 π。而电压 u₂ 相位与 e₂ 的相位相同，所以 u₁ 与 u₂ 的相位差为 π，即反相。由于漏磁通量的存在并不影响电流、电压的相位关系，所以这个结论与变压器磁芯是否存在漏磁通量无关。

当变压器有负载时，若负载是纯电阻性的，u₁ 与 u₂ 的相位差为 π 的结论仍然成立。若电路是电感性（或电容性的），则副线圈上的电流 i₂ 和端电压 u₂ 不再是同相位的。电流 i₂ 的磁通量反馈到变压器中去，将改变 e₁（或 u₁）与 i₀ 的相位关系，则 u₁ 和 u₂ 相差为 π 的关系一般不再成立。

为了讨论变流比公式，在无漏磁通量情况下，两个线圈 1 和线圈 2 的自感系数 L₁、L₂、互感系数 M 与线圈 n₁、n₂ 之间的关系为 M = n₂\(\frac{{{L_1}}}{{{n_1}}}\) = n₁\(\frac{{{L_2}}}{{{L_2}}}\) = \(\sqrt {{L_1}{L_2}} \)。若有漏磁通量存在，M 值将比 \(\sqrt {{L_1}{L_2}} \) 小。

当变压器有负载时，原、副线圈内的电流均在磁芯中激起磁通量，产生互感现象。没无铜损、铁损和漏磁通量，且线圈的绕向如图 3–11 所示（这时，原、副线圈在铁芯中激起的磁通量方向相同）；原、副线圈的电流、线圈匝数、自感系数分别为 i₁、n₁、L₁ 和 i₂、n₂、L₂，互感系数为 M；并设负载是纯电阻性的。

令 i₁ʹ = i₁ – i₀，i₁ʹ 称为反射电流，它是由于负载电流 i₂ 的存在而在原线圈内增加的电流，其作用是抵消电流 i₂ 在原线圈中增加的磁通量。i₁ʹ 和 i₂ 的有效值满足 \(\frac{{{I_1}^\prime }}{{{I_2}}}\) = \(\frac{{{n_2}}}{{{n_1}}}\)。

通常情况下，虽然原线圈电感 L₁ 很大，I₀ 很小，但 I₀ 总是存在的（约为满载电流的 3 % ~ 8 %）。所以 I₁ʹ ≠ I₁，I₁ 为原线圈中实际电流的有效值。只有当 L₁→∞ 时，I₀→0，才有 I₁ʹ = I₁，即原线圈电流全部为反射电流，因而 \(\frac{{{I_1}}}{{{I_2}}}\) = \(\frac{{{n_2}}}{{{n_1}}}\)。这就是中学物理教材中的变流比公式。由上面的推导可见，它成立的条件是很严格的，要求变压器无铜损、铁损、无漏磁．且原线圈电感 L₁→∞。

建立理想变压器模型的目的是突出变压器的基本原理，对通常的实际问题作简化的近似处理。因此，变压比和变流比公式对于理想变压器应该是严格成立的。从上述推导过程可以看出，同时满足下列四个条件的变压器，可定义为理想变压器：

①没有漏磁，即通过原、副线圈的每一匝的磁通量都一样；

②原、副线圈没有电阻，即忽略线圈导线中的焦耳损耗（铜损）；

③铁芯中没有铁损，即忽略铁芯中的磁滞损耗和涡流损耗；

④原、副线圈的感抗均趋于无穷大，从而空载电流趋于 0。（在上面的讨论中，只涉及原线圈的电感趋于无穷大。但在许多情况下，两个线圈中任一个作原线圈都是可以的，所以要求两线圈电感均趋于无穷大。）

4．教科书图 3.2–5 低频扼流圈用来“通直流，阻交流”的演示实验

（1）方法一

电路如图 3–13 所示。电源使用 6 V 干电池和 2 V、50 Hz 交流电源（学生实验电源）串联，组成直流与交流成分均有的电源。电感 L 可以用可拆变压器的次级线圈或其他电感线圈，L 的直流电阻为 R_L，可用欧姆表测出。R₁、R₂、R₃ 为电阻箱。R_L 与电阻 R₃ 之和等于电阻 R₁ 与 R₂ 之和，且 R₁ = R_L，R₂ = R₃。

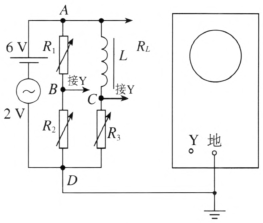
示波器 Y 轴输入耦合开关置于“DC”，在没有输入的情况下，X 扫描频率 10 ~ 100 Hz，并且将扫描线置于示波器方格坐标的中央，作为 0 参考点。首先将 A 点接 Y 轴，学生电源交流电压置于 2 V，电源开关置于关的位置，这时 6 V 直流电源已经通过学生电源的 2 V 线圈将 6 V 直流电压加到示波器的 Y 轴，在示波器上扫描线高于（或低于）坐标轴 0 参考点，记下该位置的格数。然后仍在交流电源开关断开的情况下，分别将 B、C 两点接入示波器 Y 轴，观察扫描线偏离 X 轴0 参考点的位置．这两个位置分别是 R₂ 与 R₁ 的分压值的位置和 R₃ 与 R_L 的分压值的位置，并记下这两个位置的格数，可以发现它们是相同的。

将学生电源开关接通电源，用示波器观察三个位置的电压波形：

①电源电压波形，即 R₁ + R₂ 两端的电压波形。这时可以看到交流电压波形是以 6 V 直流电压所在位置为横轴的正弦波形；

②观察 R₂ 部分的电压波形，可以看到交流电压是以 B 点直流电压为横轴的正弦波形；

③观察 R₃ 上的电压波形，该处是以 C 点直流电压位置为横轴的交流电压波形。但是其交流电压幅度小于 B 点位置的交流电压幅度。

实际观察情况举例。电感用小型变压器的次级线圈，其直流电阻 R_L = 10 Ω；R₃ 为 10 Ω；电阻箱 R₁ 调整为 10 Ω，电阻箱 R₂ 调整为 10 Ω；直流电压 6 V、交流电压 2 V；学生示波器 Y 轴衰减“×100”挡，X 轴扫描频率 10 ~ 100 Hz，微调扫描频率，出现 2、3 个波形。波形如图 3–14 所示，图中的尺寸相同。甲图为 0 参考点；乙图为 6 V 直流电压的位置，约大于 0 参考点 1 大格；丙图为 A 点电压波形即电源电压波形；丁图为电阻 R₂、R₃ 上的直流电压分压的位置，其大小约为乙图的一半；戊图为电阻 R₂ 上的电压波形，是以丁图为横轴的正弦交流电压波形；己图为电阻 R₃ 上的电压波形，是以丁图为横轴的正弦交流电压波形，其幅度小于戊图的幅度，因为通过 R₃ 上的交变电流受到电感 R_L 的阻碍作用。

（2）方法二

只用图 3–13 中电感 L 与电阻 R₃ 的串联电路（不用 R₁ 和 R₂），分为两次实验。第一次使用直流电源，观察示波器显示的电源电压大小（变化格数）和电阻 R₃ 两端的电压大小（变化格数）。第二次将电源改为交变电流，电压大小与直流电源相同，先观察交流电压大小（可以数峰值的格数），再观察电阻 R₃ 两端的交流电压大小。比较两次 R₃ 上的电压与电源电压之比，可知电感 L 对直流和交变电流有不同的作用。

5．电磁式（动铁式）仪表

磁电式（动圈式）仪表不能直接测量交变电流。常用的交流电表有两类：一类是整流式仪表，是用二极管将交流整流成为直流后接入磁电式仪表进行显示，多用电表中的交流电压挡、交流电流挡都是这样的。另一类是电磁式仪表。

电磁式仪表的结构如图 3–15 所示。被测交变电流通入固定的线圈，当电流 I 的方向如图所示时，定、动两软铁片都被磁化，且磁极方向相同，因而互相推斥使动铁片转动，直到游丝产生的反力矩和推斥力矩平衡为止。电流越强，推斥力矩越大，指针偏转角度越大。当电流方向改变时，两铁片磁化后的极性都和图中相反，仍然互相推斥，所以指针仍保持在原来偏转的角度处。这种仪表按有效值刻度，由于刻度是不均匀的，精度较低，适合测量工频交变电流，多用于工业上的测量，如配电盘（柜）上的电压表、电流表就是电磁式仪表。

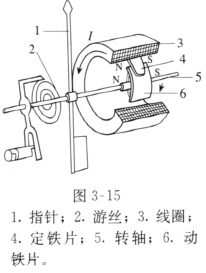
电磁式仪表也可以测量直流。

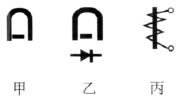
图 3–16 所示的是在电表的度盘上标明它们类型的图形符号，甲表示磁电式，乙表示整流式，丙表示电磁式。

6．J 2423 可拆变压器的简易实验

（1）观察可拆变压器的构造，了解 J 2423 型可拆变压器主要由以下几部分组成：

铁芯：由硅钢片叠压铆合的 U 形铁芯及条形铁轭组成闭合磁路。

线圈骨架：方形胶木制成，上沿有铝制线圈的匝数标牌和接线柱。

线圈：L₁ 总匝数 1 400 匝，在 200 匝和 800 匝处抽头，抽头引线接于接线柱上，标号分别为 0、2、8、14；L₂ 共 400 匝，在 100 匝处抽头，接线柱上标号分别为 0、1、4。

（2）在“0–1”两接线柱间串联一个指示灯泡和 12 V 直流电源，在“0–14”两接线柱间接上白炽灯泡。指示灯泡发光，表明在初级线圈中有电流通过。注意观察次级线圈上白炽灯是否发光。

思考直流电能不能通过变压器由初级传送到次级？

（3）初级电路不变，把次级电路灯泡换成氖泡。电路接通后，指示灯发光，注意氖泡是否发光。把初级电路断开，注意初级电路断开的瞬间，氖泡是否发光。

思考初级电路断开，即初级线圈的电流发生变化时，次级电路有没有电压产生？

（4）在“0–1”接线柱间接上 12 V 交流电源，在“0–14”接上额定电压是 220 V 的白炽灯泡。注意观察白炽灯是否发光。

思考交变电流能不能通过变压器由初级传送到次级？能不能改变交变电流的电压？在这一实验中电压是升高了还是降低了？

（5）把“0–14”接线柱串联白炽灯沲后接在 220 V 交流电源上，在“0–1”接线柱间接上指示灯泡，将条形铁芯取下，接通电源后初级灯泡发光，次级灯泡不发光。然后将条形铁芯从 U 形铁芯的一端向另一端推移，同时注意指示灯是否发光或发光的情况。

思考变压器铁芯的情况对电能从初级电路传送到次级电路有无影响？在这一实验中，传到次级的交变电流电压是升高了还是降低了？

注意事项：

①接线时应断开电源，谨防触电。

②变压器线圈严禁不插铁芯接在电源上。因为不插入铁芯，线圈本身的电感很小，感抗小而电流很大，极易烧坏线圈。

发布时间：2025/9/10 下午9:39:33  阅读次数：178