选择性必修一 第三章 机械波 参考资料

1．惠更斯原理

（1）惠更斯原理的表述

惠更斯原理是关于波面传播的理论，它的表述可通过图 3–12 来说明。我们考虑在某一时刻 t 由振源发出的波扰动传播到了波面 S₁。惠更斯提出：S₁ 上的每一面元可认为是次波的波源。由面元发出的次波向四面八方传播，在以后的时刻 tʹ 形成次波面。在各向同性的均匀介质中，次波面是半径 r = vΔt 的球面，这里 v 为波速，Δt = tʹ − t。惠更斯认为：这些次波面的包络面 S₂ 就是 tʹ 时刻总扰动的波面。

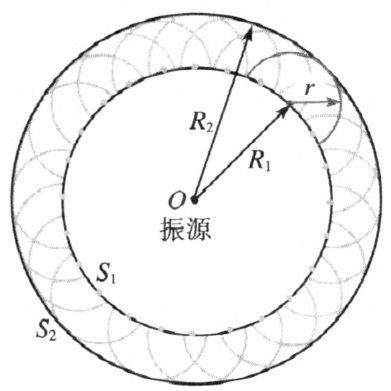
（2）对反射定律和折射定律的解释

根据惠更斯原理，可以解释光的反射定律和折射定律。下面就来论证这个问题。

如图 3–13 所示，一列平面波到达两种介质的界面，AB 是这列波的一个波面。由于入射波的传播方向与界面并不垂直，a、c、b 三条波线并不同时到达界面，它们到达界面时产生子波的时间也就有先有后，子波传播的距离也就有远有近。当波面上的 B 点刚刚到达界面上的 Bʹ 点时，A、Cʹ 两点发出的子波的波面如图中两小段圆弧所示，它们的包络面为图中的 AʹBʹ，这是反射后新的波面，aʹ、cʹ、bʹ 三条射线与波面 AʹBʹ 垂直，是反射波的波线，代表了反射波的传播方向。

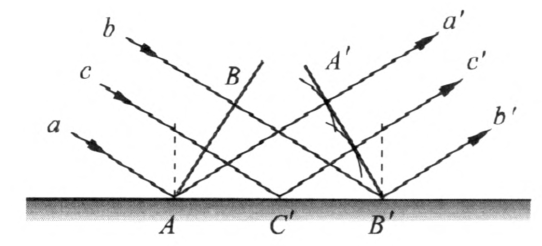
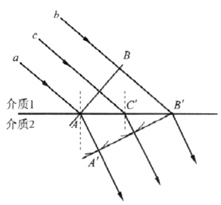
当波由一种介质进入另一种介质时，如图 3–14 所示，一束平面波中的波线 a 首先于 t 时刻由介质 1 到达界面。波线 a 进入介质 2 后，又经过时间 Δt，波线 b 也到达界面。这时 A、Cʹ 两点发出的子波的波面如图中两小段圆弧所示，它们的包络面为图中的 AʹBʹ，这是波进入介质 2 之后的新的波面。由于是两种不同的介质，其中波的传播速度 v₁、v₂ 不一定相同，在 Δt 这段时间内，两条波线 a 和 b 前进的距离 AAʹ 和 BBʹ 也不一定相同。因此波进入第二种介质后传播方向常常发生偏折。这是波的折射现象。

2．简谐波的波函数

为了定量地描述介质中波动的情况，必须求得介质中各质元的位移与该质元所处的平衡位置及时间的定量关系。这种定量关系就是波的表达式，也叫作波函数。我们只讨论简谐波的波函数及图像。

设有一波前为平面的简谐波，在均匀介质中沿 x 轴的正方向传播，波速为 v。由于这是一种平面波，所以在与 x 轴垂直的平面上，各点的振动情况是一样的，因此只要讨论 x 轴上各点的振动，就可以知道空间中各点的情况。

以 O 点为波源，设该处质元做简谐运动，其位移 u 与时间 t 的关系为

\[u = A\cos \omega t\]

式中 A 为振幅，ω 为角频率。考察波线 Ox 上的任意一点 P，它离 O 点的距离为 x，当波源的振动传到 P 点时，P 点的质元将重复 O 点质元的振动，角频率也相同，但振动的相位要落后于 O 点。因为 O 点的振动传到 P 点需时长 \(\frac{x}{v}\)，所以 P 点质元在时刻 t 的振动相位和 O 点质元在时刻 tʹ = t − \(\frac{x}{v}\) 的振动相位一样，即其相位为

\[\omega t' = \omega (t - \frac{x}{v})\]

考虑到平面简谐波侍播时各质元的振幅相等，P 点质元在时刻 t 的位移为

\[u = A\cos \omega t' = A\cos \omega (t - \frac{x}{v})\tag{1}\]

这就是平面简谐波的波函数。因 ω = \(\frac{{2\pi }}{T}\)，vT = λ，ν = \(\frac{1}{T}\)，故波函数也可写为

\[u = A\cos 2\pi (\frac{t}{T} - \frac{x}{\lambda })\tag{2}\]

或

\[u = A\cos 2\pi (\nu t - \frac{x}{\lambda })\tag{3}\]

如令 k = \(\frac{{2\pi }}{\lambda }\)，则波函数还可写为

\[u = A\cos (\omega t - kx)\tag{4}\]

式中 k 称为角波数，单位为 rad/m。

从波函数中可见，当振幅 A、角频率 ω 和波速 v 确定后，位移 u 是质元所处平衡位置 x 和时间 t 的函数，即波函数有 x 和 t 两个自变量。

在波线上某一确定位置，即指定 x，位移 u 就只是时间 t 的函数，此时，波函数描述位于 x 处的质元的振动情况。

在某一确定时刻，即 t 一定时，位移 u 仅是 x 的函数。此时，波函数描述在特定时刻 x 轴（波线）上各质元的振动位移的分布情况，而连接 x 轴上各质元位移的曲线就是此时的波形图。

3．水波

水波是一种常见的波，形成水波的回复力不是弹性力，而是水的表面张力和重力。微风拂过，水面形成的涟漪细波主要是表面张力作用的结果。这种波叫表面张力波，它的波长很短，一般不大于几厘米。海面上飓风劲吹产生的大波或洋底地震引起的海啸，波长为几米、几百米甚至几百千米。这种巨浪振荡的回复力主要是重力。这种波叫重力波。下面只简要介绍有较重要实际意义的重力波。

水有深浅之别。对水波来说，深浅是相对于水波波长来说的。水的深度 h 远小于波长 λ 时为浅水。研究指出，浅水面上水波波速 u 和波长无关，只由深度决定，其关系为

\[u = \sqrt {gh}\;\;\; (h \ll \lambda )\]

例如，由洋底地震引起的海啸的波长一般为 100 ~ 400 km。太平洋的平均深度为 4.3 km，对海啸来说，太平洋算是浅水，因此海啸在太平洋上的传播速度

\[u = \sqrt {9.8 \times 4.3 \times {{10}^3}} \;{\rm{m/s}} = 205\;{\rm{m/s}} = 738\;{\rm{km/h}}\]

这大约等于现今大型喷气式客机的飞行速度！

对于深水，即 h ≫ λ 的情况，研究指出，水面波的波速和波长有关，其关系为

\[u = \sqrt {\frac{{g\lambda }}{{2\pi }}}\;\;\; (h \gg \lambda )\]

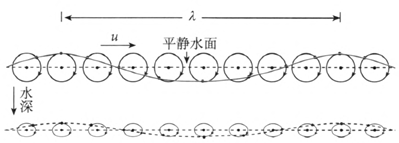
不管是浅水波还是深水波，水面上水的质元的运动都不是上下的简谐运动而是圆周运动。水面下水的质元的运动是椭圆运动，越深运动范围越小（图 3–15）。这样．水波的波形图并不是正弦曲线。

4．地震波

地震是一种严重的自然灾害，它起源于地壳内岩层的突然破裂。一年内全球大概发生约百万次地震，但绝大多数不能被人感知而只能由地震仪记录到，只有少数（几十次）造成或大或小的灾难。

发生岩层破裂的震源一般在地表下几千米到几百千米的地方，震源正上方地表的那一点叫震中。从震源和震中发出的地震波在地球内部有两种形式：纵波和横波，它们被地震学家分别称为 P 波（首波）和 S 波（次波）。P 波的传播速度从地壳内的 5×10³ m/s 到地幔深处的 14×10³ m/s。S 波的速度较小，约 3×10³ ~ 8×10³ m/s。两种波速的区别被用来计算震源的位置。P 波和 S 波传到地球表面时会发生反射，反射时会产生沿地表传播的表面波。表面波也有两种形式：一种是扭曲波，使地表发生扭曲；另一种使地表上下波动，就像大洋面上的水波那样。P 波、S 波以及表面波的到达都可以用地震仪在不同时刻记录下来（图 3–16）。

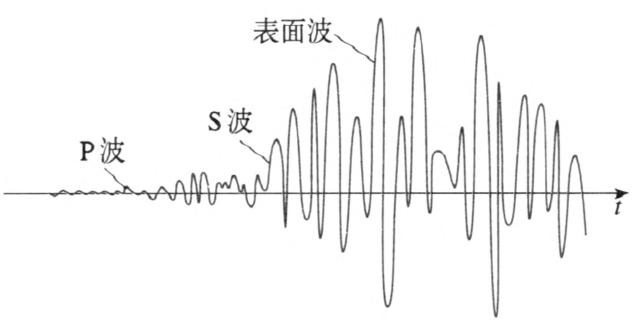
地震波的振幅可以达到几米（例如，1976 年唐山大地震时地表起伏超过 1 m），因而能造成巨大灾害。地震会释放巨大的能量，例如，一次里氏 7 级地震释放的能量约为 10¹⁵ J，这大约相当于百万吨级氢弹爆炸所放出的能量。

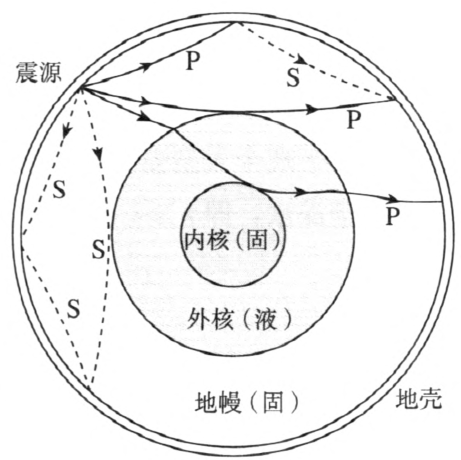
地震波中的 P 波可以在固体和液体中传播，而 S 波则只能在固体中传播（因为液体不可能发生切变），它们又都能在固体和液体交界面处反射或折射。因此，通过对地震波的详细分析可以推知它们传播所经过的介质分布情况。目前对地球内部结构的认识几乎全部来自对地震波的分析（图 3–17）。人造地震可以帮助科学家了解地壳内地层的分布，它是石油和天然气勘探的一种重要手段。此外，对地震波的分析也是检测地下核试验的一种可靠方法。

5．多普勒效应与击波

让我们以点波源为例来说明。设 S 为一个点波源，其频率为 f₀。在均匀且各向同性的介质中发出球面波．等相面（例如波峰面）是以 S 为中心的球面，设 u 代表介质中波速的大小。

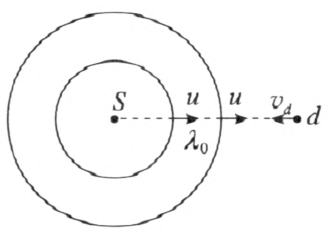
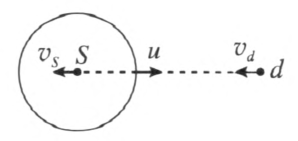
如图 3–18 所示，先考虑静止于均匀介质中的点波源 S，S 每隔一个周期 T₀ = \(\frac{1}{{{f_0}}}\) 向外发出一个等相面（球面），等相面以速度 u 向外传播，相邻两等相面间的距离为波长 λ₀，u = λ₀f₀。如果观察者从 d 沿 S、d 连线向 S 运动，速度为 v_d，则等相面相对观察者的运动速度为 u + v_d。相邻等相面经过观察者的时间即周期 T = \(\frac{\lambda }{{u + {v_d}}}\) = \(\frac{1}{f}\)，所以 f = \(\frac{{u + {v_d}}}{u}\)f₀ > f₀。如果观察者远离波源运动，则 f = \(\frac{{u - {v_d}}}{u}\)f₀ < f₀。观察者感到的波的频率变化是等相面相对于观察者的速度变化产生的。

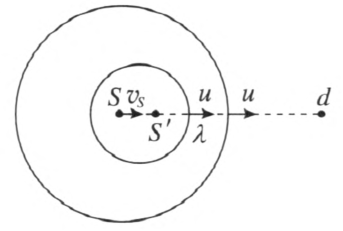
再考虑波源在介质中运动速度为 v_S，观察者静止，v_S 指向观察者方向。某一时刻，波源 S 发出的等相面仍是以S为球心的球面、传播速度仍是 u。但是，因为波源的运动，等相面的分布不再均匀，波长 λ 因而与方向有关。经过一个周期 T₀，波源 S 运动到位置 Sʹ，位移为 v_ST₀，如图 3–19 所示。在连线方向上，相邻两等相面间的距离，即波长 λ = λ₀ − v_ST₀，所以，观察者感受到波的周期 T = \(\frac{\lambda }{u}\) = \(\frac{{u - {v_S}}}{u}\)T₀，f = \(\frac{1}{T}\) = \(\frac{u}{{u - {v_S}}}\)f₀ > f₀。如果波源远离观察者运动，λʹ = λ₀ + v_ST₀，则 f = \(\frac{u}{{u + {v_S}}}\)f₀ < f₀。观察者感受到的波的频率变化是波长变化引起的。

应该注意，无论是观察者运动还是波源运动，相对于介质而言，波的传播速度都是 u。当观察者和波源都沿它们的连线运动时，如图 3–20 所示，观察者感受到的波速 uʹ = u + v_d，波长 λʹ = λ₀ + v_ST₀，所以，频率

\[f = \frac{{u'}}{{\lambda '}} = \frac{{u + {v_d}}}{{u + {v_S}}}{f_0}\tag{1}\]

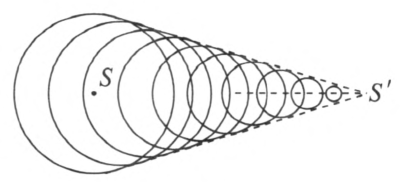
（1）式只适用于波源速度小于介质中波速的情况。如果波源速度超过介质中的波速，一系列从大到小的球形等相面形成一个圆锥，圆锥的顶点为波源 S，如图 3–21 所示。圆锥的侧表面是这组球面的包络面，叫作马赫锥。

通常定义 M = \(\frac{{{v_S}}}{u}\) 为马赫数，即波源速度相对于介质中波速的倍数。马赫数是空气动力学中的重要参数，超音速飞机的马赫数大于 1。例如，波音 747 大型客机的马赫数达 0.88，仍是亚音速。

马赫锥对应着因波源高速运动而在介质中产生的一种特殊波动——击波。这种波动在介质中意味着突发性扰动．并引起介质内压强、密度陡变。超音速飞机从头顶飞过时，人们总是先看到飞机，在击波未到达时听不到引擎的轰鸣声。当击波到来时，人们会听到一声短暂的巨响，称作声爆。实际上，这不是一次而是两次压强陡变。人们先体验了一次飞机前部击波引起的压强陡变，而后是一次机尾击波导致的压强陡变，只不过两次陡变的间隔太短（大约 \(\frac{1}{{50}}\) s），听起来好像仅有一次轰鸣。击波引起的压强陡变，有可能导致沿途建筑物的轻微损坏，例如击碎玻璃，所以，超音速飞机只允许在无人居住区上空进行超音速飞行。

击波是一种普遍存在的现象。只要波源运动的速度超过周围介质中的相应波速，都会存在一个特征锥面，短暂的大幅振动就发生在锥面到达的地方。在静水中游泳的鸭子，身后会留下两条后掠的尾迹，说明鸭子的游泳速度超过水表面波的波速。高速开过水面的快艇留下的燕尾迹，也说明水面击波的存在，由于水面波有色散，尾迹间的夹角恒约为 39°，与艇速无关。

6．光波的多普勒效应

光波（电磁波）作为一种波动，也存在多普勒效应。但是，因为电磁波的传播可以在真空中进行，而不依赖任何介质的存在，因此，不应当再利用介质参考系来解释这种波的多普勒效应，应该依靠的是狭义相对论中因惯性系间相对运动导致时间膨胀的结论。

我们仅以最简单的情况为例进行推导。

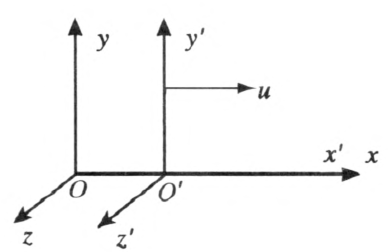
以恒定速度 u 沿着惯性参考系 S 的 x 轴方向运动的光源 Oʹ，在与它相对静止的惯性参考系 Sʹ 上发出周期性光脉冲，周期为 T₀，频率为 f₀ = \(\frac{1}{{{T_0}}}\)。由于时间膨胀，在 S 系上测量光波的周期对应的时间 Δt 满足

\[\Delta t = \frac{{{T_0}}}{{\sqrt {1 - {\beta ^2}} }}\tag{2}\]

其中 β = \(\frac{u}{c}\)。注意到此时间间隔是用 S 系内不同位置的钟测得的，所以 Δt 尚不是 S 上某个特定观察者测得的光波周期。为了得到同一个观察者，例如观察者 O 测得的光脉冲的周期值，还需要考虑光源 Oʹ 运动所带来的影响。譬如设光源 Oʹ 远离 S 系上的观察者 O 而去，如图 3–22 所示。Oʹ 发出的相邻光脉冲到达观察者 O 还需要多走过一段距离 uΔt。所以，观察者 O 测得光脉冲的周期 T 为

\[T = \Delta t + \frac{{u\Delta t}}{c} = \Delta t(1 + \beta )\tag{3}\]

把（2）式代入（3）式后则得到

\[T = {T_0}\sqrt {\frac{{1 + \beta }}{{1 - \beta }}} \]

或改写成相应的频率关系

\[f = \frac{1}{T} = \sqrt {\frac{{1 - \beta }}{{1 + \beta }}} {f_0}\tag{4}\]

这就是光波（或电磁波）的（纵向）多普勒效应公式。它表明，在我们所考虑的情况下，因光源远离观察者而导致 f < f₀，观察者收到的频率小于波源频率，此现象称作多普勒红移。显然，如果波源改作朝向观察者而来，在（3）式中应把“+”换成“−”，从而导致相应的公式为（4）式中分子、分母换位，结果 f > f₀，即发生所谓多普勒蓝移。还可以看出，对光波多普勒效应的解释，不用像弹性波那样引入介质参考系，起作用的只是光源与观察者之间的相对速度，不必计较究竟是哪个在运动。

根据星体光谱发生红移还是蓝移，可以判断星体远离还是朝向我们运动，再通过相关计算可以求出星体的运动速率。这已经成为天文观测中测晕星体运动速度的基本方法。例如，1917 年斯利弗拍摄到 15 个涡旋星系的光谱，并发现其中 13 个星系的吸收光谱向红端移动了。这一现象说明，星系在离我们而去，根据各个星系的相对频移推算出它们的运行速率，有的可达 6.4×10⁵ km/s。

7．多普勒超声诊断

超声波的多普勒效应可以用来研究心脏和大血管中血液的动力学特性，它已成为临床心脏病诊断的一项重要手段。

利用超声波的多普勒效应测定血流速度的原理如图 3–23 所示。超声探头产生一束频率为 1 ~ 10 MHz 的超声波束，遇到运动中的血细胞（称为声靶）时，沿发射方向返回，再被探头所接收。

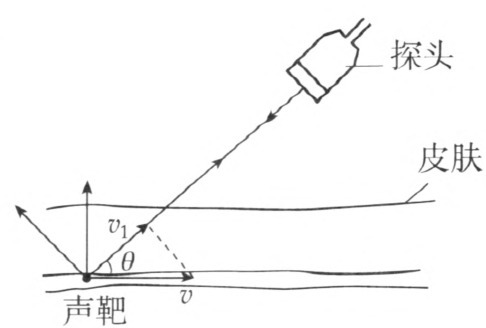
如果探头发射的超声波频率为 f₀，血流速度为 v，血的流速与超声波束之间的夹角为 θ，超声波在人体组织内的传播速度为 u，则接收器接收到的频率 f 与 f₀ 的差值（多普勒频移）为

\[{f_{\rm{D}}} = f - {f_0} = 2{f_0}\frac{{{v_1}}}{u} = 2{f_0}\frac{{v\cos \theta }}{u}\]

为了获得最大频移信号，在进行多普勒超声心动图检查时，应使超声波束与血流方向尽可能地平行，这样 cosθ ≈ ±1。在 f₀ 和 v 已知的条件下，只要测得频移值 f_D，就可知道血流速度 v。血流速度是诊断的重要依据之一。

8．演示横波的形成和传播

演示波的形成和传播有两类教具，一类演示真实波，另一类演示模拟波。教学时，应当先给学生演示真实波的现象，再结合模拟演示分析波的特点。通常学校会配有波动演示器，它是一种组合式的仪器，既可演示横波，又可演示纵波；既可演示真实波的现象，又可进行模拟演示。该仪器的详细使用方法参见仪器说明书。

下面介绍一些较为简易的演示方法。

（1）用橡皮绳演示横波

理论上，用橡皮绳演示横波现象最为直观，但由于脉冲传播速度过快以及反射波的干扰，演示现象很不明显。教学时．宜用线密度较大、张力较小的橡皮绳。可用直径 10 mm、长 6 m 左右的乳胶管，在管内填入密度较大的金属颗粒或粉粒（如铁粉和铅粒），并每隔 1.5 ~ 2 cm 用线结扎起来．其结构如图 3–24 所示。

演示时，将橡皮绳的一端拴在门框（或窗框）上，手执另一端。先使橡皮绳静止，再用手上下抖动一次，可以看到一个脉冲沿绳传播，还可以看到反射现象。

也可把橡皮绳平放在地面上或长桌面上，让两个人各持橡皮绳的一端。把绳适当拉紧，一个人猛地向上抖一下，使有一个半波脉冲向对方传播；两个人同时抖动一下，使出现相向传播的两个脉冲波，在相遇时出现叠加现象。由此可以演示波的独立传播和叠加原理。

（2）利用弹性体扭曲形变的传播制作简单的横波演示器

如图 3–25 所示，将 2 条长约 1.2 m 的宽松紧带并在一起，每隔约 5 cm 用针钉两条线，使两线之间可以穿过一根筷子（共横穿二十多根筷子）．在每根筷子的两端各固定一个泡沫塑料小球，再将松紧带的两端固定在支架上。调节支架间的距离，使松紧带的松紧适度（不要过紧）。调节每边的小球成水平直线。演示时，拨动一端的小球使其上下振动，则其余的小球顺序振动而形成横波。

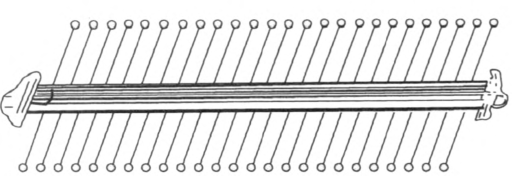
用该装置还可以演示两列波的独立传播和相遇时的叠加现象。

（3）模拟横波演示器

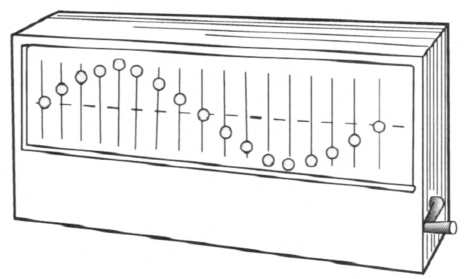
箱式模拟横波演示器的外形如图 3–26 所示。逆时针转动摇柄，演示屏上的质点就排成一条水平线；顺时针转动摇柄，各个质点就依次竖直振动起来。教师可以用它来配合讲解，说明波的特点，也可以说明波的图像。

9．演示水波的传播

（1）用发波水槽可以演示水波的反射、折射、衍射和干涉现象。水波演示器利用薄膜气泵产生频率可调的气脉冲作为波源，而且用频闪光将水波投影至半透明屏上，闪光的频率也可以调节，从而使水波看似以缓慢的速度传播，或使波形静止，以利于观察。

（2）如没有现成的仪器，可以自制。图 3–27 是利用电磁打点计时器改装的振源，图 3–28 是用玩具电动机加上偏心轮制作的振源。

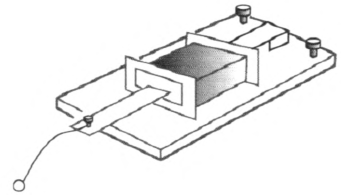
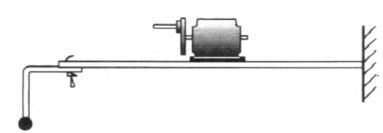
水波槽的周边应向外倾斜，内壁贴上软泡沫塑料或棉纱布以减弱反射波的干扰。

（3）做波的反射实验时，用点振源产生圆形波。在波的传播方向上放置一条挡板，首先让振子打击一下水面，可以看到圆形的波面向前传播，遇挡板后反射回来。然后再让振子连续振动，观察传播和反射现象。这样可以观察得更清楚一些。

换上条形振子，按同样的程序，可以演示直线波的反射现象。

（4）知果在波的传播方向上放置两条挡板，中间留一定宽度的间隙，可以看到波的衍射现象。

（5）演示折射现象时，在水下放一块玻璃板，厚度大约为 5 mm，使浅水区的水深大约为 2 mm，用条形振子产生直线波，并使深水区与浅水区分界线的法线与直线波的传播方向成一锐角，可以看到水波从深水区到浅水区后波面折过一定的角度，且波长变短。

（6）演示波的干涉时，为使现象清晰，应注意调节振子离开水面的高度、振动的频率和振幅，以及频闪光的频率。

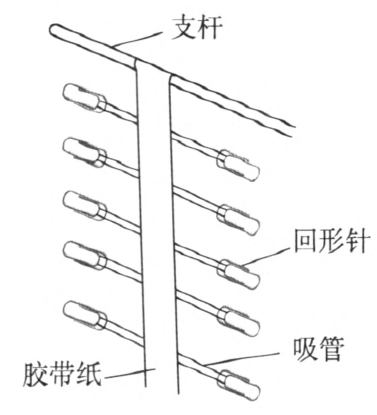
10．制作简易的横波实验器

仪器的结构如图 3–29 所示。使用大约 24 根饮料吸管、若干回形针和一条胶带纸。展开胶带纸，每隔 25 mm 左右粘一根吸管。每根吸管两端各别上一个回形针。把胶带的一端挂在铁架台的横杆上，拨动上端（或下端）的吸管，使回形针左右振动，就可以看到横波的传播现象。

发布时间：2025/8/30 下午1:03:27  阅读次数：78