选择性必修一 第二章 机械振动 参考资料

1．振动是普遍存在的物理运动形式

人类生活在运动的世界里，机械运动是最直观的物理运动形式，在机械运动中，除了物体发生平动和转动之外，比较常见的运动就是振动和波动了。人类生活中，到处都有振动的例子。人们乘车、船以及飞机会感到振动；工厂中大型机械运转时，机器甚至厂房会振动；农民在耕种时，农具会振动；甚至地球本身也在不时地因地壳运动而振动着。广义而言，人体内心脏的跳动、肺的扩张和收缩等也在一定意义上属于振动；交流电路中的电流和电压围绕着一定的数值往复变化，也是一种振动。振动现象比比皆是。

有的振动有利，有的振动有害。人们广泛地应用着有利的振动。日常生活中，人们须臾不可离开的各种计时装置利用着振动，通信、电视以及发电等是电磁振动在不同领域中的具体体现。中学物理教学中常举的共振筛、理发推以及播种机是对机械振动的应用。振动的有害方面也不少。人们需要安静的工作环境时，周围街道上的车辆移动甚至都会成为一种干扰。在工厂的生产中，有害振动更是多见。例如，大型化工厂的空气压缩机一般都安装在钢结构的厂房里。当卧式活塞空气压缩机运转时，活塞做水平方向的往复运动。活塞来回运动一次，机器和厂房构成的整个系绕的质心也相应地在水平方向来回运动一次，这导致厂房自身的质心在水平方向做相应的往复运动。同样地，机器竖直方向的往复运动，也会导致与其固连的厂房相应地上下振动。如果厂房设计得不合理，或者在合理设计的厂房内随便变更空气压缩机的转速，都有可能导致厂房的振动加剧，甚至产生受迫振动下的共振现象，使厂房形变过大发生损坏甚至坍塌。此外，还有有害的自激共振现象。风吹过烟囱或桥梁，在适当的风速和建筑物尺寸下，就会发生破坏性的自激共振。1953 年在美国有一只直径为 5 m、高约 90 m 的焊接烟囱，在风速约为 16 m/s 的强风持续吹动下，以 1 Hz 的固有频率发生自激共振。共振后不久，烟囱就发生挠曲，并且形成了一个大裂缝。对于有害的振动，根据其发生机理，可以加装特定的隔振装置或采取防振措施加以抑制或消除。

2．振动的分类

振动的分类方式是多种多样的。按照是否能够用一个时间参数的周期函数来描述系统的响应，可以把振动分为周期振动和非周期振动。

按照激励的给予方式，周期振动又可以分为自由振动和非自由振动。所谓自由振动是指系统受到初次激励后，再没有外界激励时产生的振动。一次性获得必需的能量输入后，系统振动过程的特征由其本身的固有性质（如质量、弹簧的劲度系数、摆长以及阻尼等）决定。简谐运动和弱阻尼振动就属于自由振动。简谐运动可看成无阻尼振动，一次性激励后，振动就永远地持续下去。如果存在着引起能量损耗的任何形式的阻尼（如空气或其他介质的阻力，以及电磁阻尼等），自由振动不可能无限期地持续下去，随着能量的消耗，振幅逐渐衰减，直到完全停止。为了使振动能够维持下去，就需要外界对系统提供持续性的激励。在不同种类的持续性激励下，系统的响应表现为不同的持续振动方式，常见的有受迫振动、自激振动和参数振动等。激励是产生振动的一个必要条件，阻尼足够小（弱阻尼或无阻尼）是产生自由振动的必要条件（而不是产生振动的必要条件）。

受迫振动是系统在持续不断的周期性激励作用下的振动。这种激励与系统本身的性质无关，振动过程的特征不仅与系统的固有性质（如弹簧的劲度系数、质量和阻尼等）有关，还与激励的性质（如振幅和频率）有关。受迫振动的激励方式可能以周期力的方式，还可以有其他的形式。例如，振动系统的支撑点做简谐运动，同样可以使系统发生受迫振动。

自激振动不同于受迫振动，系统受到的不再是周期性激励。产生自激振动的系统必须有一个能源，它为系统提供一个持续的（甚至恒定不变的）激励，这个激励被系统的初始振动（通过反馈）调控为周期性的能量输入，把恒定的能源转化为周期性能源来弥补阻尼带来的损耗，使振动得以维掎。自激振动的实例很多，诸如风吹树梢飕飕作响，琴弓驱动使琴弦振颤，笛、笙等管乐器的气柱振动发声，以及人体的呼吸和心脏跳动都是自激振动的例子。

参数振动是外界通过使系统内的某个物理参数（如质量、摆长以及刚度等）发生周期性的变化而引起的振动。输入的能量同样用以弥补阻尼带来的能量损失，使振动得以维持下去。最常见的参数振动的实例恐怕就是荡秋千了。荡秋千者在摆动过程中，适时地蹲下、站起（即相位关系恰当），改变等效摆长而对摆动系统做功，人的生物能转化为机械能，周期性地输入系统，使秋千摆动不止。

除了以上谈到的各种周期振动之外，还有系统的响应不能用周期函数描述的非周期振动。非周期振动又可分为脉动响应和随机振动，它们各有自己的形态特征。脉动性的激励，例如短时间内作用在系统上的冲击力，使系统作出脉动响应，某处的位移 y 随时间的变化关系曲线可能如图 2–5 所示。核爆炸引起较远距离处的物体发生的动力学响应，如位移、加速度和应力等随时间的变化，就属于这种类型的振动。

振动的形式多种多样，其中简谐运动是最基本的。周期振动不一定是简谐运动，但是依照傅里叶定理，可以把它表示成一个傅里叶级数，即多个简谐运动的叠加。设描述周期搌动的函数为 y = y（t），t 为时间参数，T 为周期，则有

\[y(t) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty  {({a_n}\cos n\omega t + {b_n}\sin n\omega t)} \tag{1}\]

式中 ω = \(\frac{{2\pi }}{T}\)，称作基频，各项常系数满足

\[{a_n} = \frac{\omega }{\pi }\int_{ - \frac{T}{2}}^{\frac{T}{2}} {y(t)} \cos n\omega tdt\]

\[{b_n} = \frac{\omega }{\pi }\int_{ - \frac{T}{2}}^{\frac{T}{2}} {y(t)\sin } n\omega tdt\]

（n = 1，2，…）

利用三角函数公式可以把（1）中频率相同的两项合并写成一项，即

\[{a_n}\cos n\omega t + {b_n}\sin n\omega t = {C_n}\cos (n\omega t - {\varphi _n})\]

式中

\[{C_n} = \sqrt {a_n^2 + b_n^2} \]

\[\tan {\varphi _n} = \frac{{{b_n}}}{{{a_n}}}\]

这样就可以把（1）式改写成

\[y(t) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty  {{C_n}\cos (n\omega t - {\varphi _n})} \tag{2}\]

此式表明，一切周期振动均可以表示成一系列简谐运动的线性叠加，这些简谐运动的频率是基频 ω 的整数倍，称作谐频。把周期函数分解为简谐函数（正弦或余弦）的方法，叫作频谱分析。

3．简谐运动的定义

简谐运动的定义，常见的有以下三种。

（1）根据运动学的特征来定义：物体对平衡位置的位移随时间作余弦（或正弦）变化的运动，叫作简谐运动，即

\[x = A\cos (\omega t + \varphi )\]

（2）根据力的特征来定义：物体在线性回复力作用下的运动是简谐运动，线性回复力

\[F =  - kx\]

（3）采用运动微分方程来定义：简谐运动遵从的微分方程为

\[\frac{{{\rm{d}}{x^2}}}{{{\rm{d}}{t^2}}} + {\omega ^2}x = 0\]

对于这三种定义可进行以下讨论。

①定义（1）着眼于运动特征。但是，在随时间作余弦变化的驱动力作用下的稳定受迫振动的规律为

\[x = A\cos ({\omega _{\rm{f}}}t - \varphi )\]

其中 A 表示振幅，φ 表示稳定受迫振动比强迫力落后的相位，ω_f 为强迫力变化的角频率。这也同样是“位移 x 随时间作余弦变化”，然而它不属于简谐运动。这是因为余弦或正弦函数都是谐和函数，凡按正弦或余弦规律变化的运动，都叫作谐和运动。而作为一种典型的运动形式或一种有特定意义的运动模型的“简谐运动”，以它的特殊性质区别于一般的谐和运动，这就是：它的运动周期由振动系统的固有性质决定，它的振幅 A 和初相 φ 则由振动的初始条件决定。如果不考虑上述特征，只从（1）中的表达式是不可能把简谐运动从一般的谐和运动中区别出来的。

②简谐运动的第（2）（3）种定义在力学范围内是完全等价的，它们确切地定义了简谐运动这种独特的运动。由 F = − kx 和牛顿运动定律可以得到 \(\frac{{{\rm{d}}{x^2}}}{{{\rm{d}}{t^2}}}\) + ω²x = 0，对 \(\frac{{{\rm{d}}{x^2}}}{{{\rm{d}}{t^2}}}\) + ω²x = 0 积分也可以得到 x = Acos（ωt + φ），而且其中的 ω、A、φ 正好具有简谐运动才有的特性。

当把简谐运动这个运动模型推广到力学以外的领域时，\(\frac{{{\rm{d}}{x^2}}}{{{\rm{d}}{t^2}}}\) + ω²x = 0 的优点就显现出来了。

任何一个物理量 x，只要满足这个微分方程，那么这个量就随时间在某一值附近做简谐运动。例如，电磁学中由电感和电容构成的 LC 电路中发生电磁振荡时，电流 i 满足的微分方程为

\[\frac{{{\rm{d}}{i^2}}}{{{\rm{d}}{t^2}}} + \frac{i}{{LC}} = 0\]

电流 i 随时间作余弦变化

\[i = {i_0}\cos (\omega t + \varphi )\]

其中 ω = \(\sqrt {\frac{1}{{LC}}} \)，由 LC 电路的固有电学性质决定；振幅 i₀ 和初相 φ，由引起振荡的初始条件决定。由上面的式子可知，LC 电路中的电流做简谐运动，而电流的简谐运动就不好用线性回复力 F = − kx 来定义了。

可见，简谐运动的第（3）种定义十分确切，便于推广。但是中学生不熟悉微积分，这种定义显得十分抽象。在中学物理教学中，为了便于学生接受，采用 F = − kx 的定义是可以接受的。

4．相位

相位是描述振动状态的物理量。由简谐运动的位移 x = Acos（ωt + φ₀），速度 v = − Aωsin（ωt + φ₀），可以得到

\[\cos \varphi  = \frac{x}{A}\]

\[\sin \varphi  =  - \frac{v}{{\omega A}} =  - \frac{v}{{{v_{\rm{m}}}}}\]

式中的 v_m = ωA，为简谐运动速度的幅值。可见，相位 φ 所确定的是位移与振幅之比 \(\frac{x}{A}\)，以及速度与速度幅值之比 \(\frac{v}{{{v_{\rm{m}}}}}\)。

对于频率和振幅不同的简谐运动，当相位相同时，位移 x 和速度 v 并不相同，但是比值 \(\frac{x}{A}\) 和 \(\frac{v}{{{v_{\rm{m}}}}}\) 却是完全相同的。这两个比值更能反映简谐运动的振动状态的特点。例如，当物体处于正的最大位移这一运动状态时，比值 \(\frac{x}{A}\) 都等于 1，\(\frac{v}{{{v_{\rm{m}}}}}\) 都等于 0，对应的相位是 φ = 2nπ（n = 0，1，2，…）；当物体处于通过平衡位置向负方向运动这一振动状态时，比值 \(\frac{x}{A}\) = 0，\(\frac{v}{{{v_{\rm{m}}}}}\) = − 1，所对应的相位为 φ = \(\frac{\pi }{2}\) + 2nπ（n = 0，1，2，…）；如此等等。

所以，比值 \(\frac{x}{A}\) 和 \(\frac{v}{{{v_{\rm{m}}}}}\) 与一般表示运动状态的位移 x 和速度 v 相比，能更确切地描绘物体的运动状态。通常说相位是描述振动状态的量，确切地说，相位所描述的是由 \(\frac{x}{A}\) 和 \(\frac{v}{{{v_{\rm{m}}}}}\) 所表示的振动状态。这样，对振幅和周期不同的两个简谐运动，比较它们在某时刻的相位，就可以了解它们的振动状态是否相同。

5．单摆的周期

（1）非线性摆的振动周期

一根不可伸长、不计质量的绳长为 l，一端固定于 O 点，另一端系质量为 m 的小球，就可组成一个摆，如图 2–6 所示，竖直线 OP 为摆以 O 点为轴摆动的平衡位置。

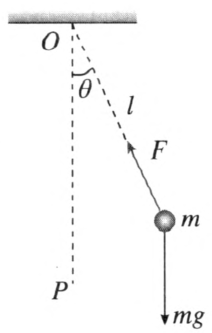
为了研究摆动的一般规律，把摆看作一个绕 O 点转动的刚体，摆对 O 轴的转动惯量 I = ml²。当角位移为 θ 时，作用于小球的重力对 O 点的力矩 M = − mglsinθ（其中的负号表示力矩的方向与角位移 θ 的方向相反）。根据定轴转动的定律

\[I\beta  = M\]

有

\[m{l^2}\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{t^2}}} =  - mgl\sin \theta \]

整理后可得

\[\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{t^2}}} + \frac{g}{l}\sin \theta  = 0\]

这是一个非线性微分方程，与简谐运动的微分方程 \(\frac{{{\rm{d}}{x^2}}}{{{\rm{d}}{t^2}}}\) + ω²x = 0 不同。因此，一般情况下，摆动不是简谐运动，而是一种非线性振动。这种摆的周期表达式为

\[T' = T\left[ {1 + \frac{1}{4}{{\sin }^2}\left( {\frac{{{\theta _0}}}{2}} \right) + \frac{9}{{64}}{{\sin }^4}\left( {\frac{{{\theta _0}}}{2}} \right) +  \cdots } \right]\]

其中 T = \(\frac{{2\pi }}{\omega }\) = 2π\(\sqrt {\frac{l}{g}} \)。

可见，一般情况下的摆的周期随摆幅（由 θ₀ 表示）的变化而变化，不是等时摆。

（2）单摆和它的周期

若摆动过程中，摆线对平衡位置的角位移 θ 的绝对值都很小，当 sinθ ≈ θ 时，\(\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{t^2}}} + \frac{g}{l}\sin \theta  = 0\) 可以近似为 \(\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{t^2}}} + {\omega ^2}\theta  = 0\)，其解为

\[\theta  = {\theta _0}\cos (\omega t + \alpha )\]

其中 θ₀ 为最大摆角，为角振幅，周期

\[T = 2\pi \sqrt {\frac{l}{g}} \]

通常所说的单摆是指一般的非线性摆在摆角很小时的情形。这是一种理想模型，周期与振幅的大小无关，是一种等时摆。

在实际应用中，在摆角足够小的条件下，就可以使用单摆的周期公式进行计算。

（3）怎样认识“摆角足够小”的条件

由摆的周期 Tʹ 的公式与单摆的周期 T 的公式的比较，可知误差

\[\eta  = \frac{{T' - T}}{T} = \frac{1}{4}{\sin ^2}\left( {\frac{{{\theta _0}}}{2}} \right)\]

θ₀ 为最大摆角。为了有一个定量的概念，在 θ₀ 为不同值时周期的误差如表 2–3所示。

从以上数字可以看到：当最大摆角在 15° 以内时，误差在 0.5% 以内；当最大摆角在 5° 以内时，误差在 0.05% 以内。

实验中还会有测量误差，如摆长测量误差、计时误差，等等。由于中学物理实验对精度要求相对不是很高，同时，系统误差的精度与测量误差的精度应该协调。因此可以认为 ，θ₀ < 15° 时即可满足中学物理实验对误差的要求。

6．人体中的振动效应

振动对人的影响有大有小，这取决于振动的振幅、频率和持续时间。已经有大量的研究来设法减小振动对人的影响。

在实验室，测量坐在硬座位上的试验者对垂直振动的反应。结果表明，反应最灵敏的频率为 6 ~ 7 Hz，当频率大约为 6 Hz 时，身体作为整体发生共振，频率比较高或比较低时则可以忍受更大的强度。

对超过 20 Hz 的情况，只要利用软垫座位和各种简单的减震装置，就比较容易使人得到保护，以免遭受强烈振动而引起的损害。然而，拖拉机和货车的振动频率通常在 1 ~ 7 Hz，而且有时振动强度较大。可以在座位下加装弹簧和液压减震器来减少振动，起到保护的效果。

与人笔直地站着或坐着相比，如果人的腿稍微弯曲一些的话，那么传到身体上部的振动就大为减少。农机的操作者有时就用这种方式站着，使得振动的强度下降。类似地，如果一个人在崎岖不平的路上骑自行车，由踏板来承受一部分或全部重量而不是由座位来承受的话，那么就可减少因振动而引起的不适。

7．用传感器和计算机描绘简谐运动的图象

描绘简谐运动图像的实验可以使用数字化实验系统中的位移传感器来完成，计算机将自动绘出振动图像。

实验装置如图 2–7 所示。用细线将位移传感器发射器垂挂在立柱上，它两端的金属环与弹簧振子的水平弹簧相连；位移传感器接收器固定在支架上，与数据采集器相连。

实验步骤如下。

1．进入通用软件实验界面，单击“组合图线”，添加“位移–图像，打开位移传感器发射器电源，并使其做简谐运动，得到实验图像后，单击“停止”。

2．选择一段“位移–时间”图像作为研究对象，单击“拟合”，选取“正弦拟合”，得到如图 2–8 所示的实验图像。

发布时间：2025/8/29 上午7:37:45  阅读次数：107