选择性必修一 第一章 动量守恒定律 参考资料

1．惠更斯生平

惠更斯（Christiaan Huygens，1629—1695） 1629 年出生于海牙，他是荷兰物理学家、天文学家、数学家。

惠更斯善于把科学实践与理论研究结合起来，形成了理论与实验相结合的工作方法与明确的物理思想。他在碰撞、钟摆、离心力、光的波动说和光学仪器等多个方面作出了贡献。

惠更斯最早取得成果的领域是数学，他研究过包络线、二次曲线、曲线求长法，并发现悬链线（摆线）与抛物线的区别，还是概率论的创始人。

在 1668—1669 年英国皇家学会碰撞问题征文悬赏中，惠更斯是得奖者之一。他详尽地研究了完全弹性碰撞问题（当时叫“对心碰撞”），去世后综合发表于《论物体的碰撞运动》（1703）中，他指出：“两个具有相同质量的物体，以相同的速度相向做对心碰撞后，两者都以相同的速度向相反方向运动。”他把这个论断作为一个公理，因为两物体的情况完全一样，没有任何理由认为它们在碰撞后的运动会有所不同。

接着，惠更斯研究了两个质量相同的物体以不同的速度发生对心碰撞的问题。他想象一个人站在以速度 u 做匀速直线运动的船上，用吊起的两个相同的钢球做碰撞实验。以船作为参考系，碰撞前两球速度的大小相等，均为 v；碰撞后，两球被弹开，它们速度的大小与碰撞前相等，仍为 u。以岸为参考系，碰撞前，一个球的速度大小为 v + u，另一个的为 v – u；碰撞后，两球的速度大小则分别为 v – u 与 v + u。于是得出结论：两个相同的小球以不同的速度发生对心碰撞后，将彼此交换速度。

惠更斯在碰撞研究中得出了“运动量”守恒原理：“两个物体所具有的运动量在碰撞中都可以增多或者减少，但是它们的量值在同一个方向的总和却保持不变，如果减去反方向的运动量的话。”惠更斯既看到了动量数值的变化，又强调了动量的矢量性，纠正了笛卡儿不考虑动量方向性的错误。他还首次提出完全弹性碰撞前后 ∑mv² 守恒的规律。

惠更斯从实践和理论上研究了钟摆及其理论。1656 年他首先将摆引入时钟，以取代过去的重力齿轮式钟。在《摆钟》（1658）及《摆式时钟或用于时钟上的摆的运动的几何证明》（1673）中，他提出了著名的单摆周期公式，并研究了复摆及其振动中心的求法。他还通过对渐伸线、渐屈线的研究找到等时线、摆线以及研究了三线摆、锥线摆、可倒摆及摆线状夹片等。

在研究摆的重心升降问题时，惠更斯发现了物体系的重心与后来欧拉称之为转动惯量的量，还引入了反馈装置。“反馈”这一物理思想今天更显得意义重大。他设计了船用钟和手表平衡发条，大大缩小了钟表的尺寸。他还用摆求出了重力加速度的准确值，并建议用秒摆的长度作为自然长度标准。

惠更斯提出了他的离心力定理，他还研究了圆周运动、摆、物体转动时的离心力以及泥球和地球转动时变扁的问题，等等。这些研究对于后来万有引力定律的建立起了促进作用。他提出过许多既有趣又有启发性的离心力问题。

他设计制造的光学和天文仪器精巧超群。例如，他磨制了透镜，改进了望远镜（用它发现了土星光环等）与显微镜，还设计了几十米长的“空中望远镜”（无管、长焦距、可消色差）、展示星空的“行星机器”（即现今天文馆雏形）等。惠更斯目镜至今仍在使用。

惠更斯在 1678 年给巴黎科学院的信和 1690 年发表的《光论》一书中都阐述了他的光波动原理，即惠更斯原理。它可以用来解释光的反射、折射等现象。《光论》中最精彩的部分是对双折射提出的模型，用球和椭球方式传播来解释寻常光和非寻常光所产生的奇异现象，书中有几十幅复杂的几何图，足以看出他的数学功底。

2．对动量守恒条件的理解

教学中，学生常常产生这样的疑问：从动量定理的表达式 FΔt = pʹ − p 来看，动量守恒的条件为什么是外力的合力为 0，而不是外力的冲量为 0？

出现这样的问题，主要是由于中学阶段学生数学知识有限，动量定理只能用初等数学表示成上式，容易使学生产生一些误解。

在普通物理中功量定理是用高等数学表示的，其微分形式和积分形式分别是

\[\frac{{\rm{d}}}{{{\rm{d}}t}}(mv) = F\]

\[m{v_2} - m{v_1} = \int_{{t_1}}^{{t_2}} {Fdt} \]

微分形式适用于变力作用下的无限小时间内的力学过程，积分形式适用于变力作用下的有限时间内的力学过程。

（1）动量守恒的含义

从中学的动量定理表达式来看，当质点所受的合力保持为 0 时，则有 mv₂ = mv₁。学生常常把质点的末动量等于初动量，即把动量“不变”误认为是动量“守恒”；从普通物理学的动量定理表达式看，当 dt 时间内合力 F = 0，有 mv = 恒矢量。这就是说，所谓动量守恒，不仅要求质点的末动量等于初动量，而且还要求在整个过程中任意两个时刻的动量都相等。

（2）对于动量守恒条件的理解

从中学动量定理表达式来看，若在 Δt 时间内有 F = 0，则 mv₂ = mv₁。由此学生会想，若合力 F = 0，则合力的冲量 I = FΔt 也必为 0，自然会得到这样的结论：合力的冲量为 0 也是动量守恒的条件。从普通物理的动量定理积分形式来看，合力 F 是被积函数，冲量 I 是函数 F 的积分值。由高等数学可知，当被积函数 F = 0 时，则积分值 \(\int_{{t_1}}^{{t_2}} {Fdt} \)  一定为 0；反之，当积分值 I = 0 时，则被积函数 F 不一定为 0。用物理语言说，即当合力冲量 I 为 0 时，质点的动量不一定守恒。例如，轻绳的一端系一小球，手握绳的另一端使小球在光滑的水平桌面上做匀速圆周运动。如果选取小球运动一周的起始和终止时刻作为运动的初态和末态，在运动一周的时间内，绳对小球拉力的冲量为 0，小球末动量等于初动量，但不能认为小球在运动过程中的动量是守恒的，原因是小球运动过程中各时刻所受的合外力不为 0。

3．动量守恒定律的适用范围比牛顿运动定律更广

近代的科学实验和理论分析都表明：在自然界中，大到天体间的相互作用，小到如质子、中子等基本粒子间的相互作用，都遵守动量守恒定律。因此，它是自然界中最重要、最普遍的客观规律之一，比牛顿运动定律的适用范围更广。例如，对于运动电荷之间的相互作用，牛顿第三定律就不适用了，但动量守恒定律仍然成立。

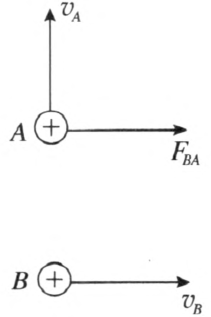
如图 1–6 所示，两个点电荷 A、B 在同一个平面内沿不同方向运动。在某一时刻，点电荷 B 通过激发的磁场作用于点电荷 A 的力为 F_BA，而点电荷 A 激发的磁场在此刻对点电荷 B 没有作用力。因此，力 F_BA 在此刻不存在反作用力，牛顿第三定律不再成立。但是，动量守恒定律仍然成立。不过，这里的动量不仅包含电荷的动量，还应包含场的动量。当我们考虑到上述这点时，动量守恒定律便是普适的定律。

4．相对论中的动量

在牛顿力学里，动量定义为 mv。根据牛顿第二定律，一个恒定的力，持续作用于一个物体，可以使该物体有任意大的速度。但是相对论告诉我们，真空中的光速是极限速度，在任何条件下物体的速度都不可能超过真空中的光速。

并且，质量也随着运动速度的增大而增大。如果用 m₀ 表示静止物体的质量，则以速度 v 运动的物体的质量 m 可以用下式表示

\[m = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\]

相对论中的动量仍定义为

\[p = mv = \frac{{{m_0}v}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\]

在采用这样定义的情况下，牛顿第二定律的表达式

\[\frac{{{\rm{d}}p}}{{{\rm{d}}t}} = F\;\;\;(F = \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{{m_0}v}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }})\]

在接近光速的情况下也同样适用了。因为随着运动速度的增大，决定物体惯性大小的质量也增大。当 v→c 时，m→∞，所以加速度趋于 0，不论力作用多长时间，速度也不会超过光速。

对于静止质量为 m₀，而速度为 c 的光子来说，它的动量 p = \(\frac{E}{c}\) 可以这样推得：

因为 E = mc²，所以

\[\begin{array}{l}{E^2} = {m^2}{c^4} = {m^2}{c^4} - {m^2}{v^2}{c^2} + {m^2}{v^2}{c^2}\\ = {m^2}{c^4}(1 - \frac{{{v^2}}}{{{c^2}}}) + {p^2}{c^2} = m_0^2{c^4} + {p^2}{c^2}\end{array}\]

在 v = c、m₀ = 0 时，E² = p²c²，所以 p = \(\frac{E}{c}\)。

5．火箭

火箭是靠发动机喷射出的工作物质（简称工质）所产生的推力作用向前推进的飞行器。将火箭和燃烧后喷出的高温高压气流视为一个系统，根据动量守恒定律，向后喷出的工质使火箭获得向前的动量，发动机连续喷射，则使火箭不断加速前进。由于火箭自身携带着能源和工质（合称推进剂），不需外界提供工质，因此可以在大气层外飞行，使人类脱离地球飞向宇宙的理想得以实现。

火箭有单级、多级之分，单级火箭难以获得发射人造地球卫星所需要的第一宇宙速度（7.9 km/s）。多级火箭一般为 2 ~ 4 级，工作时第一级火箭燃料用尽后自行脱落，第二级火箭点燃并开始工作，这样一级一级地接在一起，能够获得较好的加速性能。又因为每一级都是独立的，可以根据工作高度、条件的不同而选用不同类型的火箭发动机。但级数不宜太多，否则工作的可靠性会降低。我国目前现役的长征系列运载火箭均是多级火箭，有力保障了导航系统、空间站、探月工程以及其他深空探测项目的顺利进行。

如果不计空气阻力和重力（假定火箭在无重力的空间运动），并把火箭和由它喷出的燃气组成一个系统，那么，这个系统的动量守恒。

下面我们根据动量守恒定律，得出火箭运动的基本方程。

设在任意时刻 t，火箭主体（包括在以后的出时间内即将燃烧的燃料在内）的质量为 m，对于选定的惯性参照系的速度为 v；在 t + dt 时刻，由于已燃烧的燃料已经喷出，火箭主体的质量变为 mʹ = m + dm（由于喷出燃气，mʹ < m，故主体质量的增量为负，dm < 0），速度变为 v + dv。在时间 dt 内喷出的燃气质量为 m − mʹ = − dm，喷出的燃气相对于火箭主体的速度为 u，方向向后，则在 t + dt 时刻，燃气相对于选定惯性系的速度为 v + dv − u。由于火箭主体和喷出的燃气所组成体系的动量守恒，所以

\[mv = (m + {\rm{d}}m)(v + {\rm{d}}v) + ( - {\rm{d}}m)(v + {\rm{d}}v - u)\tag*{①}\]

化简为

\[m{\rm{d}}v =  - u{\rm{d}}m\tag*{②}\]

这就是火箭在无重力空间中运动的基本微分方程式。式中喷射相对速度 u 与燃料的化学性质和喷口的形状有关，对一定的火箭是一个常数。由于燃料不断燃烧并喷射出去，m 和 v 都是随时间而变化的。下面根据②式讨论火箭的推力和收尾速度。

（1）火箭的推力

用时间 dt 去除②式两端，得

\[m\frac{{{\rm{d}}v}}{{{\rm{d}}t}} =  - u\frac{{{\rm{d}}m}}{{{\rm{d}}t}}\tag*{③}\]

式中 m 为 t 时刻火箭主体的质量，即为 t 时刻的加速度。与牛顿第二定律比较，上式的右端就是由喷出的燃气反作用于火箭主体的力，称为火箭的推力

\[{F_推} =  - u\frac{{{\rm{d}}m}}{{{\rm{d}}t}} = u\left| {\frac{{{\rm{d}}m}}{{{\rm{d}}t}}} \right|\tag*{④}\]

\({\frac{{{\rm{d}}m}}{{{\rm{d}}t}}}\) 是火箭主体质量的增加率。由于是不断喷出质量，故 \({\frac{{{\rm{d}}m}}{{{\rm{d}}t}}}\) < 0，所以 \(\left| {\frac{{{\rm{d}}m}}{{{\rm{d}}t}}} \right|\) 表示火箭主体的质量减小率。燃料燃烧后的产物从喷口喷出，使主体质量减小，故  \(\left| {\frac{{{\rm{d}}m}}{{{\rm{d}}t}}} \right|\) 也就是燃料的消耗率。④式表明火箭的推力等于喷射相对速度和燃料的消耗率之乘积。

长征五号运载火箭在起飞时，第一级的平均喷射相对速度 u 约为 3.1 km/s，平均燃料消耗率 \(\left| {\frac{{{\rm{d}}m}}{{{\rm{d}}t}}} \right|\) 约为 340 kg/s。由④式可估算出它的平均推力 F_推 = 1.05×10⁶ N。

（2）收尾速度

将②式改写为

\[{\rm{d}}v =  - u\frac{{{\rm{d}}m}}{m}\tag*{⑤}\]

设火箭开始发动时的初始质量为 m₀，速度为 v_i；当燃料耗尽，火箭发动机停止工作（熄火）时，火箭壳体的质量为 m_s，速度——收尾速度——为 v_f。对⑤式积分

\[\int_{{v_{\rm{i}}}}^{{v_{\rm{f}}}} {dv =  - u} \int_{{v_0}}^{{m_{\rm{s}}}} {\frac{{{\rm{d}}m}}{m}} \]

得

\[{v_{\rm{f}}} = {v_{\rm{i}}} + u\ln \frac{{{m_0}}}{{{m_{\rm{s}}}}}\tag*{⑥}\]

这就是在无重力和阻力的空间中火箭的收尾速度公式。

长征五号运载火箭点火时总质量 m₀ 约为 8.50×10⁵ kg，助推器分离时质量 m_s 约为 1.62×10⁵ kg，喷射相对速度 u 约为 3 km/s。根据⑥式算出助推器分离时的收尾速度为

\[{v_{\rm{f}}} = 3\ln \frac{{8.50 \times {{10}^5}}}{{1.62 \times {{10}^5}}}\;{\rm{km/s}} = 4.97\;{\rm{km/s}}\]

这是假定无重力和阻力情况下的计算值，实际上助推器工作时不能忽略重力和阻力的影响。长征五号运载火箭助推器工作时间 t₁ 约为 173 s。如果假定它保持竖直飞行，并计入恒定的重力作用（仍不计阻力）。则在助推器分离时的速度为

\[{v_{\rm{f}}}^\prime  = {v_{\rm{f}}} - g{t_1} = 3.24\;{\rm{km/s}}\]

实际上，长征五号运载火箭在飞行十几秒后便沿着曲线飞行，重力的影响比竖直飞行小一些。

从⑥式可知，为了提高火箭的收尾速度，除了增加火箭级数来增大 v_i 外，还可以研制新型的燃料以提高燃气的喷射速度 u，以及提高质量比。

6．实验  演示反冲运动

（1）用火箭筒演示

拿一个空摩丝瓶，在其底部用大号缝衣针钻一个小洞，这样就制成了一个简易的火箭筒。

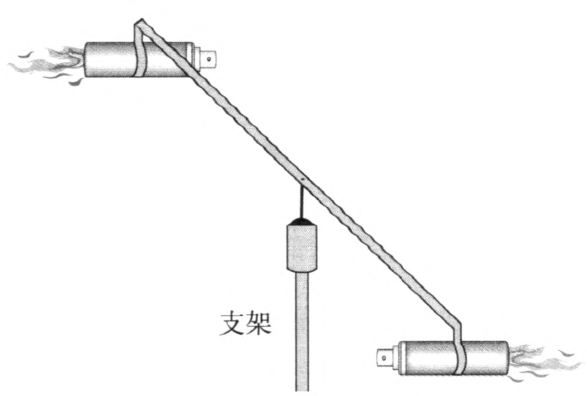
如图 1–7 所示，在铁支架的立柱顶端装上顶轴，在旋转臂的瞬侧各装一只火箭筒，再把旋转系统放在顶轴上。往火箭筒内注入约 4 mL 的酒精，并在火箭筒下方的棉球上滴少量酒精，点燃酒精棉球，火箭筒内的酒精蒸气从尾孔中喷出并被点燃。这时可以看到火箭旋转起来，带着长长的火舌，并伴随有呼呼的声响。

注意棉球上的酒精不要太多，下方的桌上不要放易燃物品。实验完毕，应将筒内剩余的酒精烧尽或倒出。

（2）火柴火箭

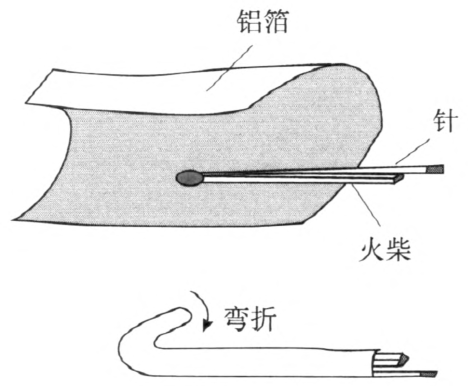
将一根火柴和一根缝被的大针并在一起，用铝箔将它们紧紧地包裹起来，再将有火柴头的一端的铝箔弯折过来密封捻紧，如图 1–8 所示。然后在靠近尾部的地方装上定向尾翼，把针拔出，就成了一个很简单的反冲火箭。

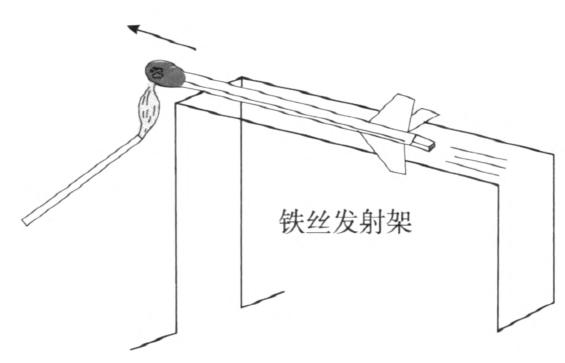
实验时，把小火箭放在铁丝架上，点燃一根火柴，对准铝箔筒包有火柴头的部位加热，当温度升高到火柴头的燃点时，箔里的火柴便被点燃，使周围的空气急剧膨胀，气体从尾口高速喷出。由于反冲作用，火箭筒便从架上向前飞了出去，如图 1–9 所示。

如果在铝箔中包两根头对头放置的火柴，两端都不封闭。将它放在架上，从中部加热。当筒内火柴点燃后，气体从两头喷出，铝箔筒仍停留在架上，从而说明了系统的动量守怛。

（3）反冲炮车

用一个现成的小玩具卡通车和一支铝壳圆珠笔的笔筒，你就能制作一辆很有趣的反冲炮车。

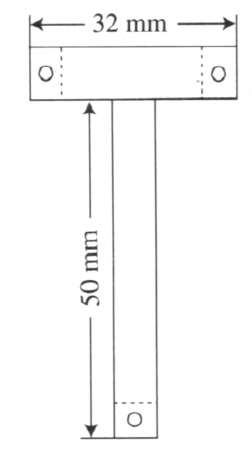
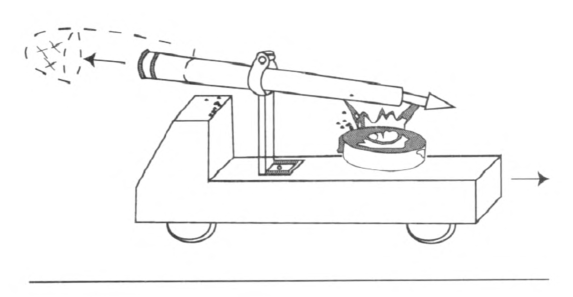
用罐头铁皮剪成如图 1–10 所示的“T”形，将上边的横边卷弯包在圆珠笔的铝筒上，并用螺丝钉或铆钉固定好。铁皮的直边作为支架，固定在卡通车的平板上，如图 1–11 所示。实验时在铝筒内放入几颗火柴头，用小塞子把铝筒口堵上，然后在铝筒封闭端下的铁盒里放一小团浸有酒精的棉花。点燃棉花，对铝筒加热，不一会儿，塞子就从炮口冲出，小车向后倒退。如果在炮口前方加一个收集罩，“炮弹”射出后即入收集罩内，炮车几乎不动。这两种情况都说明系统在水平方向动量守恒。

发布时间：2025/8/27 上午9:53:50  阅读次数：178