第十二章 电能 能量守恒定律 参考资料
1.欧姆和欧姆定律的建立
欧姆 1787 年 3 月 16 日生于德国埃尔兰根城,父亲是锁匠。父亲自学了数学和物理方面的知识,并教给少年时期的欧姆,唤起了欧姆对科学的兴趣。16 岁时他进入埃尔兰根大学研究数学、物理与哲学,由于经济困难,中途辍学,到 1813 年才完成博士学业。欧姆是一个很有天才和科学抱负的人,他长期担任中学教师,由于缺少资料和仪器,给他的研究工作带来不少困难,但他在孤独与困难的环境中始终坚持不懈地进行科学研究,自己动手制作仪器。
欧姆对导线中的电流进行了研究。他从傅里叶发现的热传导规律——导热杆中两点间的热流正比于这两点间的温度差受到启发。因而欧姆认为,电流现象与此相仿。他猜想导线中两点之间的电流也许正比于它们之间的某种驱动力,即现在所称的电动势。欧姆花了很大的精力在这方面进行研究。开始他用伏打电堆做电源,但是因为电流不稳定,效果不好。后来他接受别人的建议改用温差电池做电源,从而保证了电流的稳定性。但是如何测量电流的大小,这在当时还是一个没有解决的难题。开始,欧姆利用电流的热效应,用热胀冷缩的方法来测量电流,但这种方法难以得到精确的结果。后来他把奥斯特关于电流磁效应的发现和库仑扭秤结合起来,巧妙地设计了一个电流扭秤,用一根扭丝悬挂一个磁针,让通电导线和磁针都沿子午线方向平行放置,再用铋和铜温差电池,一端浸在沸水中,另一端浸在碎冰中,并用两个水银槽做电极,与铜线相连。当导线中通过电流时,磁针的偏转角与导线中的电流成正比。实验中他用粗细相同、长度不同的八根铜导线进行了测量,得出了如下的等式
\[X = \frac{a}{{b + x}}\]
式中 X 为磁效应强度,即电流的大小;a 是与激发力(温度差)有关的常数,即电动势;x 表示导线的长度,b 是与电路其余部分的电阻有关的常数,b + x 实际上表示电路的总电阻。这个结果于 1826 年发表。1827 年欧姆又在《动电电路的数学研究》一书中,把他的实验规律总结成如下公式
\[S = \gamma E\]
式中 S 表示电流;E 表示电动力,即导线两端的电势差;γ 为导线对电流的传导率,其倒数即为电阻。
欧姆定律发现初期,许多物理学家不能正确理解和评价这一发现,并提出怀疑和尖锐的批评。研究成果被忽视,加上经济极其困难,使欧姆精神抑郁。直到 1841 年英国皇家学会授予他最高荣誉的科普利金牌,才引起德国科学界的重视。
欧姆在自己的许多著作里还证明了:电阻与导体的长度成正比,与导体的横截面积和传导性成反比;在稳定电流的情况下,电荷不仅在导体的表面上,而且在导体的整个截面上运动。
2.欧姆定律的微观解释
由于自由电子与晶格结点频繁碰撞时,向各方向散射的机会均等,平均定向运动速度为 0,所以自由电子的热运动并不能产生电荷的集体定向运动,因而不可能形成电流。但是,如果有某种外源存在,使金属中存在一定方向的电场,则在电场作用下,自由电子将在热运动的基础上得到一个与电场方向相反的附加定向运动速度。图 12–21 表示一个电子在某一段时间内的运动,图中实线表示在无电场时自由电子的热运动情形,虚线表示有电场时自由电子的热运动情形。自由电子集体逆电场方向定向运动的现象称为漂移,这种漂移运动的平均速度称为漂移速度,用 u 表示。
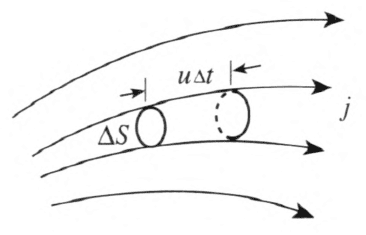
我们来看 u 与 j 的关系。在导体中取一小导体元(图 12–22),并设导体内单位体积内自由电子数为 n,则在 Δt 时间内流过导体元的电荷量为 Δq = neuΔtΔS,则
\[j = \frac{{\Delta I}}{{\Delta S}} = \frac{{\Delta q}}{{\Delta S\Delta t}} = neu\]
由于自由电子的漂移速度与电场反向,因而与 j 反向,故有
\[\boldsymbol{j} = - ne\boldsymbol{u}\tag*{①}\]
下面我们研究 u 与导体中的电场强度 E 的关系。类似气体分子动理论,自由电子连续两次与晶格骨架的碰撞之间通过的路程和经历的时间,分别用电子的平均自由程 \({\overline \lambda }\) 和平均自由飞行时间 \({\overline \tau }\) 来描写,故自由电子热运动的平均速率为
\[\overline v = \frac{{\overline \lambda }}{{\overline \tau }}\]
由于热运动不引起自由电子的定向运动,可以把两次碰撞之间,自由电子在恒定电场 E 作用下的运动看作初速度为 0 的匀加速运动,a = \(\frac{{eE}}{m}\)。设自由电子与正离子碰前的定向速率为 ut,平均定向漂移速度为 u,则有
\[{u_t} = a\overline \tau = \frac{{eE\overline \lambda }}{{m\overline v }}\]
\[u = \frac{{{u_t}}}{2} = \frac{{eE\overline \lambda }}{{2m\overline v }}\]
由于漂移速度与电场强度方向相反,故得
\[\boldsymbol{u} = - \frac{{eE\overline \lambda }}{{2m\overline v }}\tag*{②}\]
由①和②两式得
\[\boldsymbol{j} = \frac{{n{e^2}\overline \lambda }}{{2m\overline v }}\boldsymbol{E}\tag*{③}\]
一定的金属在确定温度下,n、\({\overline \lambda }\)、\({\overline v }\) 为恒量,故③式表明,电流密度 j 与导体中的电场强度成正比(微分形式的欧姆定律)。可见,欧姆定律是自由电子在外电场作用下运动的必然结果。
3.焦耳定律的微观解释
电子在电场作用下得到的与漂移速度有关的动能为
\[\overline {{E_{\rm{k}}}} = \frac{1}{2}m\overline {u_t^2} = \frac{1}{2}\frac{{{e^2}{E^2}{{\overline \lambda }^2}}}{{m{{\overline v }^2}}}\]
由于电子在碰撞后平均定向运动速度为 0,所以上式所决定的动能就是碰撞时传递给金属的动能。
设在单位时间内,每一电子平均碰撞 \(\overline Z \) 次,由气体分子动理论可知
\[\overline Z = \frac{{\overline \lambda }}{{\overline v }}\]
在单位时间内,金属单位体积内的自由电子由碰撞而传给金属的总能量为
\[p = \overline {{E_{\rm{k}}}} \cdot \overline Z \cdot n = \frac{{n{e^2}\overline \lambda }}{{2m\overline v }}{E^2}\]
4.常用的电池及其电动势
常用的电池有干电池、蓄电池、氧化银电池、锂电池等,这几种电池都是化学电池。
(1)干电池
干电池有许多种,例如锌–锰、碱性锌–锰、锌–空气等类型。其中应用最广泛的是锌–锰干电池。锌–锰干电池的负极是用锌做成的圆筒,正极是碳棒,用 NH4C1 做电解液,MnO2 做去极剂。
锌–锰干电池中的基本化学反应是
Zn + 2NH4Cl + 2MnO2 → Zn(NH3)2Cl2 + Mn2O3 + H2O
这种干电池,不论体积多大,电动势都是 1.5 V,内阻约 0.1 Ω。干电池在使用过程中,由于不断在锌极表面产生 Zn(NH3)2Cl2,电池内阻不断增大。当内阻增大到不能供给电流时,电池就报废了。一般锌一锰干电池只适用于间歇放电,而且放电电流皮在 1 A 以下。
干电池有圆筒形的和叠层的。圆筒形的用“R”表示,通常按其体积的大小又分为 1 号、2 号、3 号、4 号、5 号等几种。叠层电池用符号“F”表示,例如“4F22”表示由 4 个扁平形 F22 叠层电池组合成的电池。叠层电池是将糊状电解层涂敷在优质纸上做成的。市场上所售的高能电池多为此种电池。
下表是几种常用的锌–锰干电池的性能。
| 电池种类及型号 | 开路电压 V | 正常使用时的 放电电流/A |
容量/(A·h) | 主要用途 |
| 干电池 R20(1号) R14(2号) R6(5号) |
1.5 1.5 1.5 |
0.3 0.3 0.3 |
4.25 1.5 0.425 |
收音机 照明 一般实验 |
| 叠层电池 4F22 6F22 |
6 9 |
0.01 0.01 |
0.35 0.31 |
收音机 仪表 |
(2)蓄电池
蓄电池是能反复充电、放电的电池。最常用的是铅蓄电池,它广泛用于汽车或拖拉机的启动、通信电源、电力系统、蓄电池车及仪器设备等。
铅蓄电池的正负极板一般是用铅或铅合金制成的板栅,在板栅上填充作为活性物质的膏状物。正极板上的活性物质是 PbO2,负极板上的活性物质是海绵状铅。用硫酸溶液做电解液。
新的铅蓄电池一般在使用前需要进行初充电。首先按照制造厂规定的密度灌注硫酸溶液。注液后的反应热会引起温升,需放置 1 ~ 6 h 进行降温。反应后液面下降时,要进行补液。待温度降至 35 ℃ 以下时,便可开始初充电。初充电的电流要小,可用 20 小时率的电流(即充电电流 = 电池容量 / 20 h),充电 70 ~ 80 h。当电解液温度升至 45 ℃ 时,要减小充电电流,或暂时停止充电。在气体开始激烈产生之后,每隔 1 h 测量一次电池的电压和溶液浓度,连续三次不变时,初充电即可结束。
蓄电池在使用过程中,由于电池放电,硫酸溶液密度逐渐降低。在密度降至 1.16 g/cm3、电动势降至 1.85 V 时,必须重新充电。充电至大量产生气体后,每隔 10 ~ 15 min 测量一次电池的电压和硫酸溶液的密度。当连续测量三次不变时,充电即可结束。
铅蓄电池的内阻很小,当外电路电阻很小或电路短路时,将有很大的电流通过电池,这会损坏极板,所以一定要注意防止这种情况发生。蓄电池闲置不用时,每月也要充电一次,每次充电时间 1 ~ 2 h。
(3)微型电池
微型电池是体积很小的电池,它们的形状有纽扣形、圆柱形、硬币形等。微型电池的种类有 20 多种,例如常用的氧化银电池、汞电池、锂电池等。
氧化银电池是微型电池中用得最多的一种,广泛用于助听器、电子手表、微型计算器中。氧化银电池的正极是氧化银,负极是锌,电解液是氢氧化钾,电池放电时的反应是
正极:Ag2O + H2O + 2e→2Ag + 2OH−
负极:Zn + 2OH−→Zn(OH)2 + 2e
氧化银电池的电动势为 1.55 ~ 1.6 V,工作电压一般稳定在 1.5 V。它的突出优点是容量大(为铅蓄电池的 3 ~ 4 倍),能保持稳定的工作电压。
5.欧姆表表盘的刻度
由教科书图 12.2–6 可知,当红、黑表笔间接入某一电阻 Rx 时,通过电流表的电流为
\[I = \frac{E}{{{R_{\rm{g}}} + {R_1} + r + {R_x}}}\]
由于干电池的内阻 r 跟 Rg、R1 相比很小,可以忽略不计,所以上式可简化为
\[I = \frac{E}{{{R_{\rm{g}}} + {R_1} + {R_x}}}\tag*{①}\]
在电源电动势 E、电流表内阻 Rg、限流电阻 R1 确定的情况下,I 随 Rx 而变,电流表指针偏转的角度与 Rx 的值相对应,此即为欧姆表的原理。
如果把红、黑表笔短接(Rx = 0),调节 R1 的值使电路中的电流等于电流表的满偏电流 Ig,则
\[{I_{\rm{g}}} = \frac{E}{{{R_{\rm{g}}} + {R_1}}}\tag*{②}\]
即欧姆表的零阻值刻度应标在电流表满刻度处。
如果把红、黑表笔断开(Rx = ∞),电路中电流 I = 0,电流表指针不发生偏转,因此,欧姆表的无限大电阻刻度应在电流表的电流为 0 处。
表盘上的 0 < Rx < ∞ 之间的刻度又怎样确定呢?
首先确定中值电阻。由①和②式可知,当 Rx = Rg + R1 时,I = \(\frac{1}{2}\)Ig,即电流表指针只偏转满刻度的一半,也就是在欧姆表表盘的中央刻度处。此刻度值叫中值电阻 R中,R中 = Rg + R1。
再根据 I = \(I = \frac{E}{{{R_中} + {R_x}}}\) = \(I = \frac{R_中}{{{R_中} + {R_x}}}\)Ig 确定其他刻度。当 Rx 分别为 R中 中的 2 倍、3 倍、4 倍……时,电路中的电流 I 分别为满偏电流 Ig 的 \(\frac{1}{3}\)、\(\frac{1}{4}\)、\(\frac{1}{5}\)……即电流表指针偏转的角度分别为满偏电流时偏转角度的 \(\frac{1}{3}\)、\(\frac{1}{4}\)、\(\frac{1}{5}\)……当 Rx 的值为 R中 的 、、……时,指针偏转的角度分别为满偏的 \(\frac{2}{3}\)、\(\frac{3}{4}\)、\(\frac{4}{5}\)……所以欧姆表表盘的刻度是不均匀的。
为了使欧姆表各挡共用一个刻度标尺,一般都以 R×1 挡的中值电阻为标准,成 10 倍地扩大。如果 R×1 挡的中值电阻 R中 = 10 Ω,此时表的总内阻 r总 = Rg + R1 = R中 = 10 Ω,Rx = 10 Ω 的刻度应在刻度盘的中央。当表的 r总 = 100 Ω 时,R中 = 100 Ω,此时 Rx = 100 Ω 的刻度也应在刻度盘的中央,即指针指在原来“10”的位置,读数乘 10 就是 100 Ω,这就是 R×10 挡。依此类推。可见,扩大欧姆表的量程就是扩大表的总内阻 r总 的值。这实际上是通过欧姆表内的另一附加电路来实现的。
由 I = 还可看出,当 Rx ≪ R中,I ≈ Ig,此时指针接近满偏,Rx 变化时,I 的变化很小,表头受本身灵敏度限制,指针变化不易分辨,因而测量误差很大。当 Rx ≫ R中 时,I ≈ 0,同理测量误差也很大。所以实际上通常只用表盘中间的一段来测量,一般取 0.1R中 ~ 10 R中 这段范围。欧姆表都有几个量程,每个量程的 R中 不同,但每个量程的可用范围基本上是 0.1R中 ~ 10 R中。如果 R中 = 10 Ω,测量范围就是 1 ~ 100 Ω;如果 R中 = 100 Ω,测量范围就是 10 ~ 1 000 Ω。
6.测未知量程的电流表的内阻和量程
(1)实验仪器的选取
有一只灵敏电流表 G,刻度盘上共有 N 格刻度而无具体示数,已知该电流表的满偏电流 Ig 约为几百微安,内阻 Rg 约为几百欧。现在要求尽可能精确而简捷地测出此表的 Ig、Rg。除 G 表外可能提供的器材有:
①电流表 A(量程 30 mA,内阻约为几十欧);
②电压表 V(量程 3 V,内阻 15 kΩ);
③滑动变阻器 R1(0 ~ 200 Ω,0.5 A);
④滑动变阻器 R2(0 ~ 20 Ω,2 A);
⑤电阻箱 R3(0 ~ 9 999.9 Ω);
⑥定值电阻 R0(50 Ω,0.1 A);
⑦电池组(E = 12 V,r ≈ 0.5 Ω);
⑧开关、导线。
(2)实验要求
①设计出测量方案,画出电路图。
②除灵敏电流表 G 外所需器材是:____________________________。(填数字代号)
③说明需要测定的物理量,列出计算方程并导出计算 Ig、Rg 的数学表达式。
方案一:
为了确保灵敏电流表 G 的安全,采用如图 12–23 所示的分压式电路来测定灵敏电流表 G 的每格刻度值 I0 和内阻 Rg。
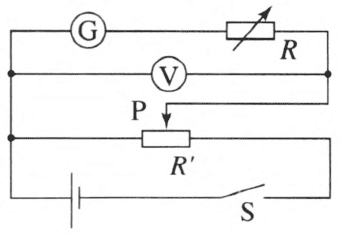
实验应选择的器材是:②④⑤⑦⑧。
调节滑动变阻器 Rʹ 和电阻箱 R,读出电压表的示数 U1、电阻箱 R 的阻值 R1、灵敏电流表 G 指针偏转刻度数 n1,然后再次调节 Rʹ 和 R,读出相应的 U2、R2 和 n2。
由欧姆定律有
\[\begin{array}{l}{n_1}{I_0}({R_{\rm{g}}} + {R_1}) = {U_1}\\{n_2}{I_0}({R_{\rm{g}}} + {R_2}) = {U_2}\end{array}\]
联立求得
\[{I_0} = \frac{{{n_1}{U_2} - {n_2}{U_1}}}{{{n_1}{n_2}({R_2} - {R_1})}}\]
此电流表的内阻是
\[{R_{\rm{g}}} = \frac{{{n_2}{R_2}{U_1} - {n_1}{R_1}{U_2}}}{{{n_1}{U_2} - {n_2}{U_1}}}\]
此电流表的量程是
\[{I_{\rm{g}}} = N{I_0} = \frac{{N({n_1}{U_2} - {n_2}{U_1})}}{{{n_1}{n_2}({R_2} - {R_1})}}\]
方案二:
为了确保灵敏黾流表 G 的安全,采用如图 12–24 所示的分压式电路来测定 G 表的每格刻度值 I0。再采用方案一中的实验电路来测灵敏电流表 G 的内阻 Rg。
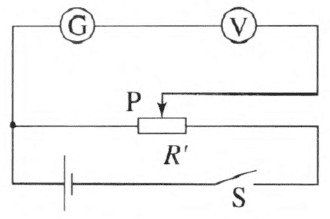
应选择的器材同方案一。
调节滑动变阻器 Rʹ,读出电压表的示数 U 和灵敏电流表 G 指针偏转的刻度数 n,由欧姆定律有灵敏电流表 G 的读数 I2 = nI0 = \(\frac{U}{{{R_{\rm{V}}}}}\)。
解得 I0 = \(\frac{U}{{{nR_{\rm{V}}}}}\)。
采用方案一中的实验电路来测灵敏电流表 G 的内阻 Rg。
调节电阻箱 R 和滑动变阻器 Rʹ,读出电压表的示数 Uʹ、电阻箱的阻值 R 和灵敏电流表 G 指针偏转的刻度数 nʹ,则
\[I = n'{I_0}\]
由欧姆定律 Uʹ = I(Rg + R),有
\[{R_g} = \frac{{U'}}{I} - R = \frac{{nU'}}{{n'U}}{R_{\rm{V}}} - R\]
联立求得结果。
7.用可调内阻的电池验证闭合电路欧姆定律
可调内阻的电池如图 12–25 甲所示,内装 1.28 g/cm3 的稀硫酸,电动势在 2 V 左右,比较稳定。利用针筒调节气压来改变电池中部通道室液面的高度来改变电池内阻。
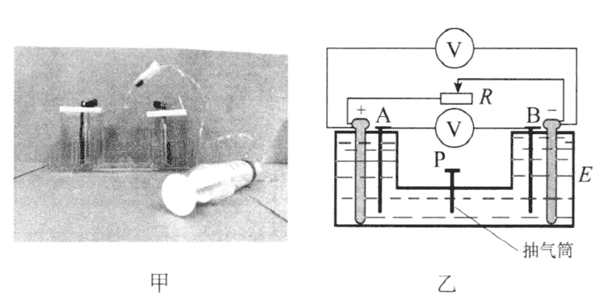
按图 12–25 乙连接电路,电压表用两个数字电压表。记下外电路断开时的读数 U外(因为数字电压表内阻可达 10 MΩ,可以认为等于电源电动势),然后每改变一次外阻 R 或电池内阻记一组 U内、U外 的数值,多测几组。
开始时测得电源电动势约为 2.100 V。
| 序号 | U外/V | U内/V | U外 + U内/V |
| 1 | 1.700 | 0.400 | 2.100 |
| 2 | 1.800 | 0.310 | 2.110 |
| 3 | 1.510 | 0.590 | 2.100 |
| 4 | 0.616 | 1.474 | 2.090 |
| 5 | 1.714 | 0.354 | 2.068 |
| 6 | 1.284 | 0.766 | 2.050 |
由实验数据可得 E = U外 + U内。
进一步分析数字电压表读数的正、负,可以看出,测电源的开路电压即电源电动势时电源正极的电势高于负极的电势,测内电压时探针 B 的电势高于探针 A 的电势,即沿电流方向不但外阻上有电势降落,内阻上同样有电势降落。
发布时间:2025/8/12 下午9:21:24 阅读次数:614
