第十一章 电路及其应用 参考资料
1.伽伐尼电
1780 年 9 月 20 日,意大利解剖学家伽伐尼在一次解剖青蛙中偶然发现,当一只剥了皮的青蛙放在起电机旁实验桌上的金属板上,解剖刀触及青蛙腿神经,若这时起电机发出电火花,青蛙腿会猛然地抽搐一下。经过反复实验,他发现用金属接触神经和发出电火花都是必要条件。伽伐尼是电的同一性的信奉者,于是想用雷电做实验。他把蛙腿用铜钩子挂到室外铁杆上,结果观察到了雷雨天蛙腿的收缩。后来,他把蛙腿提进屋内,放在一张铁桌上,当铜钩子碰上铁桌子时,蛙腿又痉挛起来,这时既无电火花又无雷电。以后他又用各种不同的金属多次重复实验,总是得到相同的结果,只是在使用某些金属时,收缩得更强烈而已。但用玻璃、橡胶、松香、干木头等来代替金属时,则不会发生这样的现象。
伽伐尼实际上已经接近了现象的要害,即电流是由两种不同金属夹以某种湿组织产生的。然而,他未能形成这样的认识,却认为是动物体内存在着“动物电”,只要用两种金属与之接触,这种电就能激发出来,就如莱顿瓶放电一样。他提出“神经电流体”假说来说明动物电的产生,认为青蛙体内存在一种“神经电流体”,是由大脑中的血液产生的,经过神经传至肌肉内部使之带正电,而肌肉外层惑应出负电。青蛙就像一只充了电的莱顿瓶,若有一种导体从外部接通神经和肌肉,“神经电流体”就会经导线弧放电,导致肌肉抽搐。
伽伐尼的发现,立即引起了人们的广泛重视,在意大利掀起了一股伽伐尼电的热潮。当时有三种观点:第一种观点认为它与莱顿瓶放电相类似;第二种观点认为伽伐尼电与普通电不同,是动物电;第三种观点根本不同意把这一现象归之于动物“神经电流体”,但人们仍称这种电流为“伽伐尼电”。
1792 年,意大利解剖学家柏林吉里做了一个实验:把青蛙腿神经截成两段,使神经末梢与上部神经分离,再用锡箔包住神经末梢,若用导线一端与锡箔接触,另一端与肌肉接触,结果发现青蛙腿部仍然抽搐。这一事实说明伽伐尼的“神经电流体”假说是不正确的。
2.伏打电堆
伏打是意大利巴维亚大学的自然哲学教授,开始时完全赞同伽伐尼的观点。后来,他改变方式重做实验,用两种不同金属构成的弧来刺激一只活青蛙,一端接触腿,一端接触背,结果青蛙也发生抽搐。这个实验事实是“神经电流体”假说所不能解释的。因为导线弧未进入肌肉,未与神经直接接触。此外,他又用莱顿瓶对一只活青蛙放电,结果也观察到青蛙的抽搐现象,表明这是外部电流刺激的结果。这样,伏打开始认力肌肉不是电的源泉,只不过起到了显示电存在的作用。
1792 年 9 月 13 日,伏打在给卡伐洛的一封信中最早提出了“接触电”的思想。他写到:用一种无可置疑的方法,即用两种不同金属相互接触的方法产生非常微弱的人工电的作用是伽伐尼电的根本原因。
1793 年,伏打对各种金属相互间的接触电动势进行了全面研究。根据测量结果,按接触电势高低顺序,他把金属和石墨排成如下顺序:锌、锡、铅、铁、黄铜、青铜、铂、银、金、水银、石墨,被称为伏打序列。
伏打还提出了中间金属定理:不论多少种不同金属串联在一起,它们的总接触电动势与中间金属无关,仅取决于两端金属的性质。
1793 年 12 月,伏打在给一家物理杂志编辑格伦的信中指出:用不同导体,特别是金属导体接触在一起,包括黄铜矿、其他矿石以及炭等,我们称之为干导体或第一类导体,再与第二类导体或湿导体接触,就会引起电激励。
1800 年春,伏打制成了有名的伏打电堆,它是用一些不同的导体按一定方式叠置起来的装置。他在给英国皇家学会的一个报告中谈到:用 30 片、40 片、60 片,甚至更多的铜片(当然最好是银片),将它们中的每一片与一片锡(最好是锌)接触,然后充一层水或导电性比水更好的食盐水、碱水等液层,或填上一层用这些液体浸透的纸皮或皮革等……就能产生相当多的电荷。
伏打电堆比莱顿瓶优越之处是能获得持续的电流。伏打的这一成就深受人们赞赏,轰动了科学界。1801 年,罗马姆用伏打电堆给莱顿瓶充电成功,证明了伽伐尼电与摩擦电是相同的。伏打电堆的发明,第一次提供了产生稳恒电流的电源,使电学研究从静电走向动电,从而开辟了一个新的研究领域。伏打电堆促进了电化学、化学电源的研究,也促进了人们研究电流的各种效应。
电流的发现工作始于伽伐尼,但发现电流的却是伏打。伏打虽然发明了电堆,但并不了解其机理,他把电堆动力的来源归结为不同金属的接触。真正阐明伏打电堆的电流来自化学作用的是英国著名化学家戴维。
3.金属中电子的热运动速度和定向移动速度
金属导体中的导电机理是自由电子的定向移动。金属中的正离子构成金属的晶体点阵,自由电子在晶格间做无规则的热运动。在导体两端加上电压后,自由电子受到电场的作用,在无规则的热运动上又加上一个定向运动,因而产生电流。自由电子的定向运动不是简单的匀速直线运动,而是在静电力作用下的加速运动,同时又不断地跟正离子碰撞,使定向运动遭到破坏,然后在静电力作用下再加速,再碰撞。从大量自由电子运动的宏观效果来看,可以认为它们是以平均速率 做定向运动。
自由电子热运动的平均速率是很大的。根据金属经典电子理论,电子的热运动和气体分子运动一样,电子热运动的平均速率 \(\overline u = \sqrt {\frac{{8kT}}{{\pi m}}} \),式中 k 是玻尔兹曼常量,k = 1.38×10−23 J/K,m 是电子的质量,m = 0.91×10−30 kg,T 是热力学温度。由公式可算出,当 t = 27 ℃,即 T = 300 K 时,
\[\overline u = \sqrt {\frac{{8 \times 1.38 \times {{10}^{ - 23}} \times 300}}{{3.14 \times 0.91 \times {{10}^{ - 30}}}}}\; {\rm{m/s}} = 1.08 \times {10^5}\;{\rm{m/s}}\]
自由电子定向运动的平均速率是很小的。假定金属导体单位体积内的电子数为 n,电子电荷量为 e,电子定向运动的速率为 \(\overline v \),在 Δt 时间内通过导体横截面 S 的电子数就是 nS\(\overline v \)Δt,通过此横截面 S 的电荷量 Δq = enS\(\overline v \)Δt,导体中的电流 I = \(\frac{{\Delta q}}{{\Delta t}}\) = enS\(\overline v \),由此可推出电子定向运动的平均速率 \(\overline v \) = \(\frac{I}{{enS}}\)。
以铜为例,铜单位体积内的电子数 n = 8.4×1022 cm−3,e = 1.6×10−19 C。直径 1 mm 的铜导线,通过的电流是 1 A 时,由上面的公式可算出这时自由电子定向运动的平均速率 \(\overline v \) = 7.4×10−5 m/s。可见自由电子定向运动的平均速率是很小的。
4.金属电阻率跟温度的关系
金属的电阻率随温度的升高而增大,当温度变化范围不大时,电阻率与温度之间近似地存在着如下的线性关系
\[\rho = {\rho _0}(1 + \alpha \Delta T)\]
式中 ρ 是温度 T 时的电阻率;ρ0 是某参考温度 T0 时的电阻率,一般常取 0 ℃ 或 20 ℃ 作为参考温度;ΔT = T – T0;α 是一个实验常数,叫作电阻率的温度系数,不同材料的电阻率温度系数不同。
根据经典电子理论推得金属的电阻率公式为 ρ = \(\frac{{2m\overline u }}{{{e^2}n\overline \lambda }}\)。式中 m、e 为电子的质量和电荷量,n 为单位体积的电子数,\(\overline u \) 为电子热运动的平均速率,\({\overline \lambda }\) 为电子的平均自由程。由于 \(\overline u = \sqrt {\frac{{8kT}}{{\pi m}}} \),所以导体的电阻率 ρ 应该跟热力学温度的平方根成正比,而不是跟热力学温度成正比,这与前面所讲的电阻率随温度变化的实验规律是不相符的。造成这一矛盾的原因,是经典金属电子论的缺陷。经典电子论认为电子的热运动服从玻尔兹曼分布规律,而自由电子的量子理论表明,电子是自旋为半整数的费米子,不服从玻尔兹曼分布,而服从费米–狄拉克统计规律,因而电阻率公式中的电子热运动平均速率 \(\overline u \) 应该用费米速度 vF 来代替,电子的平均自由程则与金属中电子的散射过程有关系。应用量子理论,可以得到电阻率 ρ 正比于 T 的结论。
5.电阻温度计
电阻温度计是利用金属电阻随温度变化的原理制作的。它利用各种金属电阻做感温元件,通过测量金属的电阻来确定温度,电阻的测量通常用惠斯通电桥。电阻温度计使用的金属有铜、镍、铂、铂铑合金等,其中以铂的测温性能最好,所以铂电阻温度计较多。
铂电阻温度计的测温范围广,常用于 – 200 ~ 600 ℃,也可延伸至 – 260 ~ 1 000 ℃。在 0 ~ 630 ℃ 范围内,铂电阻与温度的关系为
\[{R_t} = {R_0}(1 + AT + B{T^2})\]
式中 R0、A、B 为常量。
纯金属铂电阻温度计是一种非常准确可靠的仪器,常作为实用的标准温度计。
铜电阻温度计价格便宜,常用于 – 50 ~ 150 ℃。在这个范围内电阻与温度呈现线性关系
\[{R_t} = {R_0}(1 + \alpha T)\]
6.几种常见元件的伏安特性曲线
图 11–36 是镍铬合金丝的伏安特性曲线,图 11–37 是电烙铁的伏安特性曲线,都是过原点的直线,具有这种特性的元件叫线性元件。这种元件,满足欧姆定律。一般温度变化范围不大时,金属导体和电解质溶液的伏安特性曲线都是过原点的直线,都满足欧姆定律。
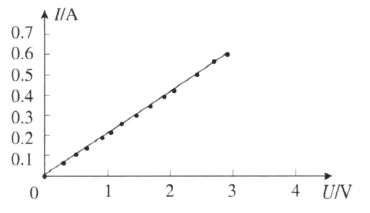
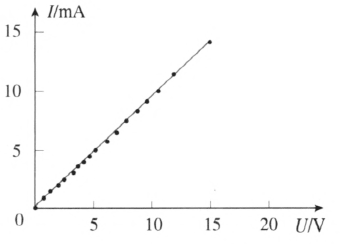
图 11–38 中“3.8 V 0.3 A”小灯泡的伏安特性曲线是一条弯曲的线。小灯泡的灯丝也是金属,但是由于其温度变化范围很大,从大约 20 ℃ 到白炽状态 2 100 ℃ 以上,灯丝电阻变化范围很大,因此电流跟电压不再成正比,是非线性元件。如果把灯丝放在恒温环境中,保持其温度不变,它的伏安特性曲线仍是过原点的直线,欧姆定律成立。顺便说一下,教师在选择或改编白炽灯的习题时要注意,不要偏离额定电压过大,否则灯泡电阻会有很大的变化。比如,给“220 V 100 W”的小灯泡加上 110 V 电压,电流是多大?这个问题中,灯泡在 220 V 和 110 V 电压下的电阻有很大差别,不可随便替代。
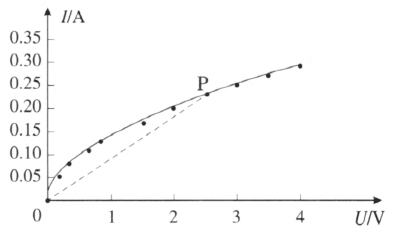
教学中发现,经常有学生认为伏安特性曲线的切线斜率表示电阻的倒数。其实不是这样的。例如图 11–38 中,在 P 状态,灯丝电阻的倒数等于 P 与原点相连的割线的斜率,灯丝电压越大,割线斜率越小,电阻越大。切线的斜率等于 \(\frac{{\Delta I}}{{\Delta U}}\),不是电阻的倒数。
图 11–39 是型号为 2CW104 的晶体二极管的伏安特性曲线,图线弯度很大,是非线性元件。
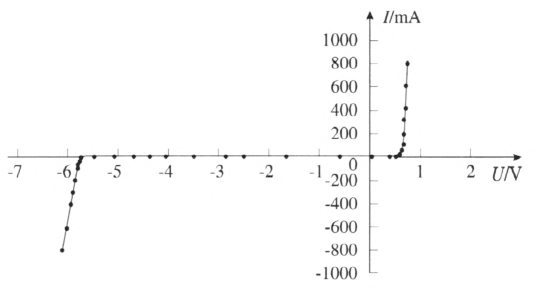
二极管的电压大约是 0.6 V 时,才有明显的正向电流通过,进入导通状态。导通后随着电压的微小增加,通过的电流急剧增大。给二极管加上反向电压时,电压低于大约 6 V 时,电流几乎为0,是不导通状态;当电压高于 6 V 时,电流急剧增加,说明二极管被反向击穿而导电。
气体也不满足欧姆定律,因为气体导电过程中,气体电离与电压有密切关系,也很难有线性范围。
对于非线性元件,电阻的定义仍然是 R = \(\frac{U}{I}\),只不过它不是常量,而是跟电流、电压有关的变量。
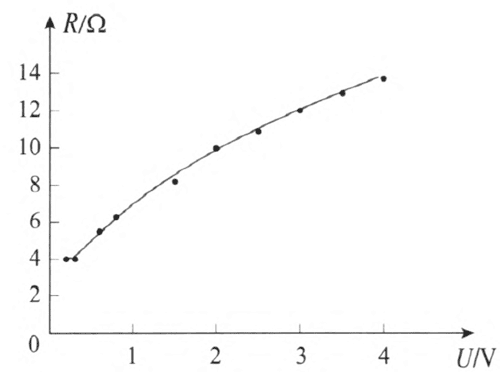
对于程度较好的学生,还可以引导学生画出小灯泡的 I–U 图像(图 11–38)和 R–U 图像(图 11–40),从图像上可以更直观地看到小灯泡电阻的变化情况,进而深入分析电阻变化的原因。
用电流传感器得到定值电阻和小灯泡通电瞬间的 I–t 图像如图 11–41、图 11–42所示。
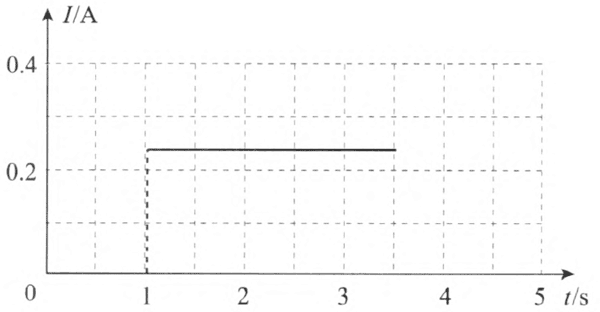
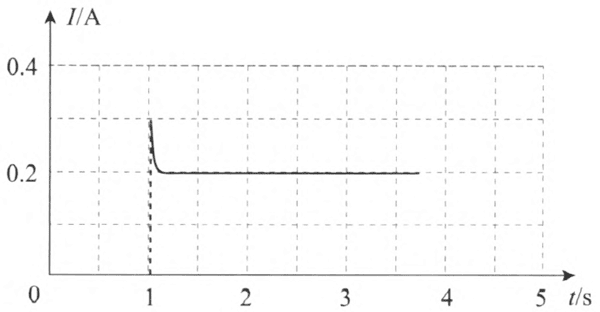
小灯泡在通电瞬间,由于温度升高很快,电阻迅速增大,电流迅速减小,因此 I–t 图像出现一个尖峰;平衡后,温度不再变化,电阻也不再变化,电流恒定。定值电阻丝的电阻率基本不随温度变化,因此通电后电流立即达到稳定。
发布时间:2025/8/5 下午9:19:51 阅读次数:532
