第十章 静电场中的能量 参考资料
1.引入电势描述静电场的必要性
电场强度 E 和电势 φ 是从不同的角度描述静电场的。各点的电场强度确定后,电场分布就已确定,用电场强度完全可以细致、准确地描述静电场。但是,有时候需要从能量的角度分析某些问题,使用电势的概念更方便。此外,电势 φ 是标量,而电场强度是矢量,标量运算比矢量运算简单。若先求出电场中各点的电势,再通过 φ 与 E 的关系求 E,也可以使问题变得较简单。基于以上两个原因,同时用电场强度和电势描述静电场。
电场强度 E 与电势 φ 之间存在一定的关系。中学物理教科书中介绍了在匀强电场中电场强度 E 与电势差 U 之间的关系,即沿电场方向 U = Ed。
一般情况下,E 与 U 的关系为
\[{U_a} = \int_a^P {E \cdot {\rm{d}} \boldsymbol{ l }} \tag*{①}\]
\[\boldsymbol{E} = - {\rm{grad}}\;U \tag*{②}\]
①式是电势定义的一般表示,它说明电势是电场强度的线积分,式中的 P、a 为积分的上、下限,P 点为电势零点。②式中的符号“grad”称为梯度,其大小等于沿等势面法线方向的变化率。如果改用极限表示,可以将②式改写为
\[\boldsymbol{E} = - \mathop {\lim }\limits_{\Delta h \to 0} \frac{{\Delta U}}{{\Delta h}} \cdot \boldsymbol{n} \tag*{③}\]
③式中的 Δh 是沿垂直于等势面方向上的位移,ΔU 为经过 Δh 后电势的变化量,以为等势面的法向单位矢量。②③式中的负号表示电场强度的方向沿电势减小的方向。
2.关于零电势的选取
(1)零电势选取的任意性及其限制
根据电势的定义,电场中任意两点的电势差 φM – φP 等于从 M 点到 P 点移动单位正电荷静电力所做的功,即
\[{\varphi _M} - {\varphi _P} = \int_M^P {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} = {\int {\left. {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} \right|} _P} - {\int {\left. {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} \right|} _M} = ( - {\int {\left. {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} \right|} _M}) - ( - {\int {\left. {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} \right|} _P})\tag*{①}\]
任一位置的电势,可表示为位置函数(\( - \int {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} \))与任一常数 C 之和
\[\varphi = - \int {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} + C\tag*{②}\]
函数(\( - \int {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} \))是确定的,常数 C 取任一实数都不会改变给定的两点间的电势差,只有预先规定电势等于 0 的位置以后,才能根据②式确定常数 C 的值,从而确定空间任一点的电势值。空间任一点 M 的电势,等于从该点移动单位正电荷到零电势点静电力所做的功,即
\[\varphi = \int_M^{零电势点} {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} \tag*{③}\]
由上所述可见,零电势点的选取是重要的,又是任意的。
但是,在一些特殊情况下,对零电势点的选取却有限制。例如,在真空中,点电荷的电势为
\[\varphi = - \int {\boldsymbol{E} \cdot {\rm{d}}\boldsymbol{l}} + C = - \frac{1}{{4\pi {\varepsilon _0}}}\int {\frac{q}{{{r^2}}} \cdot {\rm{d}}r} + C = \frac{1}{{4\pi {\varepsilon _0}}}\frac{q}{r} + C\tag*{④}\]
如果取 r = r0 处为零电势点,将 r = r0,φ = 0 代入上式,可得
\[C = - \frac{1}{{4\pi {\varepsilon _0}}}\frac{q}{{{r_0}}}\]
于是得出点电荷的电势分布为
\[\varphi = \frac{q}{{4\pi {\varepsilon _0}}}(\frac{1}{r} - \frac{1}{{{r_0}}})\tag*{⑤}\]
r0 取非零的任意实数值,都可以得到确定的电势分布。但是,如果取 r0 = 0 处(即点电荷所在处)为零电势点,就不可能确定常数 C,也就得不到确定的电势分布。所以点电荷所在的点不能取为零电势点。这种不能取为零电势的点叫作零电势的“奇点”。
在单个点电荷的情况下,如果取无限远处为零电势点,即 r0 = ∞ 处 φ = 0,则常数 C = 0,电势
\[\varphi = \frac{q}{{4\pi {\varepsilon _0}r}}\tag*{⑥}\]
表达式最为简单。
实际上,点电荷是一个物理模型,所谓无限远处,并不是数学意义上的无限远。在距带电体相当远处,就可把带电体看作点电荷。带电体的电场分布,随着距离的增大而趋于点电荷的球对称场。等势面随距离的增大而趋于球面,电场强度随 r 增大而趋于按 \(\frac{1}{{{r^2}}}\) 的规律减小。所谓物理上的无限远,就是指电场强度已减得很弱而可以忽略不计的地方。这些地方对带电体来说是无限大的球形等势面。规定 φ = 0,就是规定这个无限大的球形等势面的电势为 0。
(2)φ地 = 0 与 φ∞ = 0 的等效性
在实际问题中,常取大地的电势为 0,即 φ地 = 0,凡接地的导体电势皆为 0,这样做的原因是地球可以看作一个极大的(对通常的带电体来说是无限大的)导体球。一般带电体与地球接通,可能流入(或流出)地面的电荷量知引起地球电势的变化 Δφ地 = \(\frac{1}{{4\pi {\varepsilon _0}}}\frac{{\Delta q}}{{{r_1}}}\) 极小,而可以忽略不计(因为 Δq 很小,而 r地 极大)。地面附近的带电体由于静电感应引起的地球电荷分布的变化也是极小,因而可以忽略不计的。所以地球是一个电势稳定的大导体,以大地作为电势的参考,并规定地球的电势为 0 是很方便的。
实验证明,取 φ地 = 0 与 φ∞ = 0 是等效的。这是因为,地球上的一切实验都是在实验室或厂房里进行的,其尺度远小于地球,实验中的带电体激发的电场所充满的空间,只是地面上的一个局部小区域。这区域的边缘,对实验室中的带电体来说,就是物理上的无限远。就是说,对实际的带电体来说,无限远只是地面上的部分地区,这地区由地面上的各种建筑物构成,它们与地是等电势的。因此,对通常的实验,取无限远处电势为 0,与取大地的电势为 0 是等效的。
3.心脏除颤器工作原理简介
心脏中有一个窦房结,从窦房结发出的电信号在心脏内传播而形成波,窦房结为波源。这种波在离窦房结较远的地方可以看成平面波。这种波的传播控制着心脏的正常跳动,正常的心律被称为窦性心律。心脏纤颤是指心肌纤维的高频颤动;心房纤颤(房颤)造成心律不齐,可能引起心脑血管阻塞;心室纤颤非常严重时,可使心脏不能工作,几分钟即可致人死亡。
心室纤颤的治疗方法是用一种物理的方法——除颤器。除颤器先在很短的时间内让可控的电流通过心脏,使心脏完全停止跳动,再让心脏重新起搏,这样纤颤就消失了。这种治疗方法拯救了无数人的生命,只是电击的方法有些过于激烈,病人感到很痛苦。
除颤器工作时,一般是让 100 ~ 300 J 的电能,在约 2 ms 的时间内通过病人的心脏部位。除颤器工作时的电功率在 50 ~ 150 kW 之间,这个功率是相当大的,用电池直接供电无法达到,也大大超道了一般家庭的用电功率,而除颤器还必须便于携带,那它使用了什么样的供电装置呢?
除颤器工作时的供电装置是一个 C = 70 μF 的电容器。除颤器内带有电池,先通过电子线路把电池供电的电压升高到约 U = 5 000 V,对电容器充电,充电后电容器储存的能量约为 W = \(\frac{1}{2}\)CU2 = 875 J。由于电容器电压很高,所以可以在很短的时间内释放一部分能量,通过电子线路控制放电的能量,就可以对病人进行抢救了。除颤器的核心就是这个耐压 5 000 V 以上、70 μF 的电容器,它耐压较高、容量较大,并且体积较小、重量较轻,因此需要精心设计和制造。
4.利用电容器放电测电容
深入理解电容概念,掌握利用电容器通过高电阻放电测电容的方法,学会计算曲线下面积的方法。
(1)仪器和器材
学生电源,直流电压表,电流表,滑动变阻器,简式电阻箱,电解电容器(25 V 470 ~ 1000 μF),单刀开关两个,停表,导线若干。
(2)实验原理
电容器充电后,所带电荷量 Q 与两极板间电势差 U 和电容 C 之间满足 Q = CU 的关系。U 可由直流电压表测出,Q 可由电容器放电测量。使电容器通过高电阻放电,放电电流随电容器两极板间的电压下降而减小。通过测出不同时刻的放电电流,直至 I = 0,作出放电电流 I 随时间变化的 I–t 图像,其图线下的面积即等于电容器所带电荷量 Q。由 C = \(\frac{Q}{U}\) 可求出电容器的电容。
(3)实验方法
①按图 10–15 连接好电路。滑动变阻器 Rʹ 先调在输出电压最小的位置,电阻箱 R 调至最大阻值,并串联一个定值电阻,使放电电阻的总阻值约 10 ~ 12 kΩ。电源电压选择 6 V 稳压输出。接通电源后,调节滑动变阻器 Rʹ,使电压表示数为某一确定值(如 2.5 V),然后闭合开关 S,给电容器充电。当电容器两端电压 UC 达到某一稳定电压 U 时,充电完毕。记下此时电压表和电流表的示数。
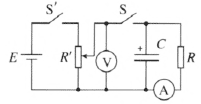
②断开开关 Sʹ 和 S,同时开始计时。这时电容器通过电阻 R 放电,放电电流 IC 随时间 t 的增加而减小。每隔 5 s 读取并记录一次电流表的电流值,直到电流消失为止。将测量结果记入下表。
| 充电电压 U1 = V |
时间 t/s | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 放电电流 IC/μA |
|||||||||||
| 充电电压 U2 = V |
时间 t/s | ||||||||||
| 放电电流 IC/μA |
|||||||||||
| 充电电压 U3 = V |
时间 t/s | ||||||||||
| 放电电流 IC/μA |
③以放电电流为纵坐标,放电时间为横坐标,在坐标纸上作充电电压为 U1 = 2.5 V 时的 IC–t 图像。图 10–16 所示为一次实验所得的 IC–t 图像。
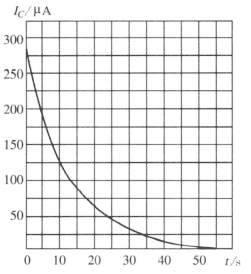
④计算实验所得图线下所围图形的面积,即可求出电容器在充电结束时所带的电荷量。具体计算方法是:首先,以坐标纸上 0.5×0.5 cm2 的一个小方格作为面积计量单位,数出实验图线下有多少个完整的小方格。对于曲线通过其中的小方格,凡曲线下的部分超过该格一半面积的记为一个小方格,不足一半的则舍去不计。这样可得到曲线下包含的小方格数。其次,确定每个小方格所对应的电荷量值,如纵轴的每一小格为 10 μA,横轴的每一小格为 5 s,则每个小方格所表示的电荷量值为 q = 10 μA×5 s = 50×10−6 C。最后,由曲线下的方格数与 q 的乘积即可得到电容器所带电荷量 Q。
⑤由电容器的电容计算公式,可计算出电容值
\[C = \frac{Q}{U}\]
⑥改变电容器的充电电压(如 U = 3 V,3.5 V),重复上述实验步骤,求出电容器的电容值(这些值应大体相近,请思考这是为什么),再取平均值,即能准确测出电容。
(4)注意事项
①应采用学生电源的稳压输出供电,不能用“直流输出”供电,因为后者存在较大的交流成分,将使开关断开的瞬间,电流表指针向右方偏转一下后再向左偏转,造成记录误差。如电源无稳压输出挡,则可在电源输出接线柱上并联一个大电容滤去交流成分,或者改用干电池组。
②放电电阻过小,放电时间短,放电电流变化快,会给记录数据带来闲难;放电电阻过大,放电时间长,放电电流变化慢,很难达到 I = 0。一般取放电电阻为 10 ~ 15 kΩ 为宜。由于简式电阻箱最大阻值为 9 999 Ω,故应串联一个定值电阻。
③同时记录放电时间和放电电流,是本实验操作上的一个难点。一般是一个同学掌握停表,每隔 5 s 读一次时间,另一同学记录相应的放电电流值。下面介绍两种简便易行的方法。
- 节拍器计时法:将节拍器的响铃周期调至 2 s(或 3 s),使它每 2 s(或 3 s)铃响一次,这样可根据铃响来记录放电电流的大小。用此法一个同学即能完成实验。
- 不论用停表还是节拍器计时,在电流表指针偏转过程中读取放电电流值都比较困难。为解决这一问题,可在电流表表盘上贴一张透明胶纸,实验时,手持泡沫笔并使笔尖随表针移动,在相应的时刻于表针位置上面一墨点(墨点在胶纸上)。待放电完毕,再由墨点位置记下相应的电流值。重新实验时可将墨点擦去,重新画点。这种方法记录的数据较为准确。
④实验中,由于电容器两端电压逐渐降低,放电电流不断减小,即放电电流,是随时间 t 变化的。因此电容器所带的电荷量 Q 不能直接用公式 Q = It 来计算。若以放电电流 I 为纵坐标,放电时间 t 为横坐标,作出 I–t 图像(图 10–17)。把横坐标 t 分成许多很小的时间间隔 Δt1,Δt2,…,Δtn,在这些小区间里放电电流可视为不变,相对应的数值 I1,I2,…,In,电容器 C 所带的电荷量为
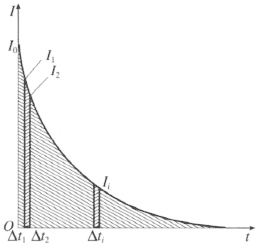
Q = I1Δt1 + I2Δt2 + … + InΔtn
式中 I1Δt1,I2Δt2,…,InΔtn 为图 10–17 中的狭条形面积。由此可知电容器 C 所带电荷量 Q 在数值上等于 I–t 图像与坐标轴所包围的面积。
5.影响静电计指针偏角 Δθ 的三个因素
(1)Δθ 与平行板电容器的电容的变化量 ΔC 有关
由于电容器的两极板分别与静电计的外壳和金属球连接(实际上是并联),所以电容器两极板间的电势差等于静电计的外壳与它的金属球之间的电势差。在 Q 不变的条件下,电容 C 减小得越多,电势差 U 增大得越多,静电计的张角变化 Δθ 也越大。由于 C = \(\frac{{\varepsilon S}}{{4\pi kd}}\),在只改变 d 的情况下,根据微分原理,ΔC = \( - \frac{{\varepsilon S}}{{4\pi k{d^2}}}\Delta d\),这说明在 d 的变化量相同时,d 的值较小时电容的变化量 ΔC 较大。在图 10–18 中可以看到,当 d1 – d0 = d2 – d1,即 Δd1 = Δd2 时,C0 – C1 > C1 – C2,即 | ΔC1 | > | ΔC2 |。可见,在电容器两极间距离较小时,改变两极间距离静电计指针偏角变化较明显。
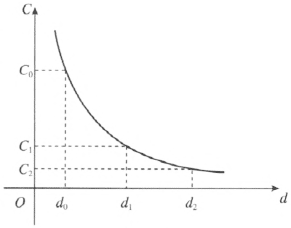
(2)Δθ 与电路中的分布电容有关
应该指出,在我们的实验中除了平行板电容器(记为 C板)外,还有静电计也是一个电容器(记为 C计),两根导线也是一个电容器(记为 C线),这三个电容器是并联的。只有当 C板 ≫ (C计 + C线)时,才可以忽略 C计 与 C线。所以,我们应该在 C板 较大的情况下进行实验,静电计指针偏角变化才会较明显。
(3)Δθ 与静电计的 U–θ 显示特性曲线有关
实验表明,静电计的指针偏转角与金属球和外壳间的电势差并不成线性关系。因此即使加在静电计上的电势差发生大小相同的变化,其指针偏转角的变化 Δθ 也是不同的。就是说 Δθ 不仅与 ΔU 有关,还与初始张角 θ0 有关,实验时取 θ0 在 15° 左右效果较好。
综上所述,为了实验取得较好的效果,建议平板直径取 20 cm 左右,两板间初始距离 d0 取 0.5 ~ 1.0 cm(这样初始电容较大)。在只改变 d 值时,d 值由 d0 增大到 10 cm 左右(超过 10 cm 时分布电容不能忽略)。实验开始时,应使静电计的指针张角 θ0 在 15° 左右。为此,给电容器极板带电时,可采用多次接触带电法,直到指针偏转 15° 左右。一旦带电过多,可用手快速触摸导线的绝缘层,让 C线 线放电,以减少极板所带的电荷量。如果做到上述几个方面,实验时,Δθ 可接近 30°,效果十分明显。在只改变正对面积或只插入电介质时,极板间距离也应在 0.5 ~ 1.0 cm,θ0 在 15° 左右。
发布时间:2025/7/31 上午9:32:48 阅读次数:966
