第八章 机械能守恒定律 参考资料
1.能量守恒定律的确立
早在 17 世纪初,伽利略提出的观点中就有机械能守恒思想的萌芽。后来,莱布尼茨又引入“活力”的概念并明确提出“活力守恒”的观念。不过,一直到 19 世纪初,始终没有哪一位科学家提出能量守恒定律。到了 19 世纪 30 年代,蒸汽机的应用帮助人们在热运动与机械运动方面积累了丰富的知识。另外,电学、化学和生物学等各方面的进展,以及人们尝试制造永动机的失败也启示人们慢慢开始想到了能量的守恒。到了 19 世纪 40 年代初,分属于不同国家、不同专业的数十位科学家,分别通过不同的途径,各自独立地在这个方面的研究中取得了进展。
1840 年,德国的迈尔在一艘从荷兰驶往东印度的船上当随船医生。当船航行到热带地区时,他发现海员患者的静脉血比在欧洲时要红。在拉瓦锡燃烧理论的启示下,他认为这是由于血液含氧较多的缘故。因为在高温的情况下,人的机体只需要吸收食物中较少的热量,所以机体中食物的燃烧过程减弱了,而在静脉血里留下了较多的氧。由此出发,迈尔认为,食物所含的化学能,就像机械能一样,可以转化为热。他还听到海员们闲谈时说,暴风雨时海水比较热,这也启发他联想到热与机械运动的相当性。他认为落体在重力影响下获得“活力”,与气体受压缩时产生热具有类似性。于是,在 1841 年航行结束后,他写了一篇论文《论力的量和质的测量》,论述各种自然力之问的相互转化。可惜由于缺少精确的实验数据而未获发表。这激励迈尔发奋自学了数学和物理,并接受朋友的劝告,决心用实验来证实自己的思想。1842 年他在德国《化学与药学年刊》杂志上发表了题为《论无机界的力》的论文。文中迈尔从“无不生有,有不变无”的哲学观念出发,得出了“力就是不灭的、能够转化的、无重量的客体”的结论。他所说的“力”就是“能量”的意思。他把这个思想运用到“落体力”(势能)、“运动的力”(动能)和热的转化与守恒,并根据气体比热的测量值,在世界上第一个得出了热的机械当量(即热功当量)为 3.58 焦耳每卡。1845 年,迈尔又自费出版了一篇更重要的论文《论有机运动与新陈代谢》。文中他首先说明了“力”的守恒和转化定律,认为它是支配宇宙的普遍规律;接着考察了 5 种不同形式的“力”,即“运动的力”“下落力”“热”“电”和“化学力”;描写了运动转化的 25 种情况,并将热功当量的值由 3.58 焦耳每卡修改为 3.60 焦耳每卡。1848 年,迈尔发表了《通俗天体力学》一文,文中他解释了陨石的发光是由于它们在大气中损失了动能,并应用能量守恒定律解释了潮汐的涨落。
焦耳是曼彻斯特一个酿酒师的儿子。为了提高他父亲所创办的酿酒厂的工作效率,他企图以电磁机(即磁电式发电机)代替蒸汽机,他很早就关心各种物理力,特别是在当时已显示出其发展前景的电力的应用价值的研究。焦耳一开始就沿着正确的道路前进,他倾力于实验工作,在 1840 年就发现了关于电流热效应的焦耳定律。在实验过程中他认识到机械、热、电、化学力等是相当的,并可以互相转化,于是他致力于热功当量的实验测定,初步成果反映在 1843 年 8 月 21 日宣读的一篇论文《磁电的热效应和热的机械值》中。可是,这里已被焦耳用实验证实了的热只是能量变换的一种形式的结论以及焦耳所透露的普遍的能量守恒定律的思想,却遭到一些物理学家的质疑。焦耳决心以更多、更精确的实验证明他的结论。1849 年 6 月,英国皇家学会刊印了焦耳的重要论文《论热的机械当量》,这是焦耳进行了摩擦生热的实验后写成的。文中焦耳总结了自己以往的工作,并介绍了现在经常被写入教材上的那个利用摩擦生热测定热功当量的经典实验。此后,焦耳还继续进行他的实验测量,一直到 1878 年,他前后用了近 40 年的时间,做了多次实验,确定了热功当量的精确数值,为能量守恒定律的建立提供了坚实可靠的实验基础。
军医出身的德国生理学家和物理学家亥姆霍兹在数学和物理上造诣深厚。他积极倡导用物理学和化学的技术来发展生理研究。他认为,生命力论实际上是赋予了生命体以永动机的性质。所以他的论证也是由永动机不可能实现入手的。在 1847 年自费出版的《论力的守恒》一书中,亥姆霍兹论述了活力守恒原理和力的守恒原理。他把永动机之不可能同中心力(即有心力)的保守性相联系,得出在这种力的作用下“系统中的张力和活力之和是始终不变的”。他所说的“张力”和“活力”就分别指的是势能和动能。亥姆霍兹把他所得出的能量守恒原理推广到光、热、电磁现象、化学运动以及生物机体内进行的过程上,指出“这一定律与自然科学中任何一个已知现象都不矛盾”。亥姆霍兹的著作中包括了迈尔的深刻思想,采用了焦耳等人的实验数据,充分地运用了精确的数学方法和严密的逻辑推理,使用了物理学家惯用的语言,因而便于被物理学家所理解和接受。他在促使人们最终确认能量守恒定律上起了重大的作用。
除了上述这三个人以外,发现能量守恒定律思想的众多科学家中还有英国的电化学家格罗夫、丹麦工程师格尔丁、法国的工程师赫因和卡诺以及德国化学家莫尔等。
2.机械功的定义和计算
机械功是所有广义功中最基本,也是最重要的一类。实际上,顾名思义,广义功的概念是由机械功推广而来的。由于机械功是系统机械能传递与转化的量度,所以把它与能量,特别是机械能分开来讨论是不可能的。以下我们把机械功简称为功。
一个质点 m,在恒力 F 的作用下发生了一段有限的直线位移 Δr,r 是质点 m 相对于所选的参考系固定的任意点 O 的位置矢量,Δr 与 F 之间的夹角为 θ,如图 8–12,则力 F 对该质点所做的功 W 被定义为
\[W = \boldsymbol{F} \cdot \Delta \boldsymbol{r} = \boldsymbol{F} \cdot \left| {\Delta \boldsymbol{F}} \right| \cdot \cos \theta \tag{1}\]
这个定义式是说,恒力对质点在一段直线位移上所做的功,等于该力与质点位移的标积,或说等于力的大小、位移的大小及力与位移间夹角的余弦三者的乘积。
由这个定义式可以讨论几个问题。
(1)质点是一种理想模型,实际中并不存在,对质点定义功,是为了概念和计算的精确。在功的定义中涉及的(线)位移,原则上也只对质点有定义。经推广,可用于做平动的刚体及一般力学系统的平动分运动。
但是,在现行的初中物理教材中没有介绍过质点模型。高中教材中虽做了介绍,但在其力学的动力学部分中根本没有使用,所以把做功与被做功的对象统称为“物体”。这样做的一个好处是,可以使初学者更容易理解“功是能量变化的量度”这一本质。“能量变化”是必定要发生在实际物体之中或实际物体之间的。
(2)凡是把被做功的对象称之为“物体”的教材,对做功过程中发生的位移都说是“力的作用点的位移”或“物体的位移”。
力的作用点也称为物体的受力点,这也是一个抽象的概念,实际中不存在物体的受力部位是一个没有尺寸大小的几何点的情况。如果物体的受力部位比较集中,那么在一定条件下可以把受力部位视为一个点,这就是力的作用点。例如,用一根细绳牵引物体,那么物体上与绳的连接部位就可以视为绳对物体的拉力的作用点。这里,绳为细绳是条件。所以,所谓“作用点的位移”,一般应理解为物体受力部位能视为质点时该质点的位移。
如上所言,位移只对点有定义。所以,所谓“物体的位移”是指物体可以视为质点时的位移。例如,对一个只做平动的刚体就可以言及它的位移,对于一般物体的平动分运动也可以言及位移。如果这样的位移是在某个力的作用下发生的,就可以用(1)式计算这个力在该位移上对物体做的功。前面已经提过,在现行的初、高中教材中都把被做功的对象称为“物体”,如说“物体在力的方向上通过的距离”“物体……在力的方向上发生一段位移”等,这里的“物体”都应理解为可以抽象成质点的。
(3)功的计算与参考系的选择有关,(1)式须对指定参考系应用。(按习惯,凡不特别说明的,都是以地面参考系为指定参考系。)
做功的两个必要因素——力和位移与参考系的关系是不同的。力学中常见的作用力,有的只和相互作用的质点间的距离有关,如万有引力(含重力)、弹性力,而摩擦力本质是分子力和库仑力,它们也是由相互作用的质点间的距离决定的。有的由宏观上看只与质点间的相对速度有关,如介质阻力。但由经典力学的伽利略变换可知,质点间的距离与彼此间的相对速度与参考系的选择无关。所以,在经典力学范围内,作用力与参考系的选择无关。但是位移作为一个运动学的量,与参考系的选择有明显的关系。这样,综合起来看,一个作用力的功有相对性,即与参考系的选择有关,这是由受力质点的位移有相对性决定的。
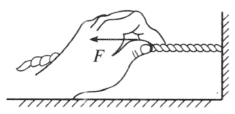
(4)在注意了功的相对性之后,再来讨论一个有关位移的问题。由于实际中被做功的对象都是有大小尺寸的物体,所以有时会发生力的作用点(受力质点)在物体上改变位置的情况。作用点的位置改变,不算为作用点对指定参考系发生位移,在这个改变上该力没有对物体做功。例如,如图 8–13 所示,手捏住一端固定于墙壁上的绳并在绳上滑动,绳上不同点顺次充当手对绳的摩擦力 F 的作用点,但各作用点均未对指定参考系(地面)发生位移,故这个摩擦力对绳不做功。又如,如图 8–14 所示,子弹头射入一固定于地面的木块中,弹孔壁上的不同点(实际上是一圈)顺次充当子弹对木块的摩擦力 F 的作用点,但各作用点均未对指定参考系发生位移,故这个摩擦力对木块不做功。但是,若木块不固定,在子弹射入并停止在其中的过程中,相对地面发生了一段直线平动位移 Δr,则在这个位移上 F 对木块做功,若将 F 视为恒力,则这个功为 F·Δr。
(5)不同的书中会出现“力做功”及“物体做功”两种提法。那么,这两种提法究竟有没有区别呢?首先应该说,从原则上讲这两种提法是通用的,没有什么不同,说物体做功,也是说物体对被做功的对象所施的力在做功。但仔细玩味,二者还是有些细微差别的。由功是能量的传递与转化的量度这一角度来看,提“物体做功”更实际一些,所以认为它只是“力做功”的简单说法似乎粗糙了一些。另外,对初中学生来说,“力做功”太抽象了,不如“物体做功”容易接受。当到了高层次的学习阶段,所遇到的做功的情况复杂起来了。用“力做功”的提法分析起来就会更精确。什么“作用力的功”“反作用力的功”“合力的功”“分力的功”等都能分得很清楚,表达得很简明。所以,“力做功”的提法会更好用。例如,对“合力的功等于诸分力功的代数和”这一定理的表述和证明,改用“物体做功”的提法就很难进行。
(6)在(1)式中,若有 \(\frac{\pi }{2}\) < θ ≤ π,则有 W < 0,即力对物体做负功。由动能定理来看,力对物体做负功,是使物体的动能减少。
在习惯上,对这个问题还有一种提法,叫做“物体克服阻力做了功”。对这种提法存在着不同的理解。例如,某书中说:“一个力对物体做了负功,是因为这个力阻碍物体的运动,成为物体运动的阻力。在这种情况下,我们也常常说成是物体克服这个力做了功(取绝对值)。所以,摩擦力对前进中的机车做负功,也可以说成是机车克服摩擦力做了功。向上抛出的物体在向上运动时,重力对物体做负功,也可以说成是物体克服重力做了功。”由这段话可以看出,这里是把这两种提法视为是两件事,在前一件事中被做了负功的物体,在后一件事中成了对外做等值正功的物体,而隐含的转换条件就是“作用力的功与反作用力的功等值异号”。但是,这条“规律”并不是普遍存在的。所以有人对此提出异议,提出了“滑动的物体在克服摩擦阻力前进的过程中,究竟是物体的哪一个力做了正功;物体在克服重力上升的过程中,究竟是物体的哪个力做了正功”等问题。
3.研究弹簧的弹性势能与形变量的关系
弹性势能无法直接测量。本实验先把弹性势能转换为物体的动能,然后通过测量物体的动能来比较原来弹性势能的大小。具体搡作步骤如下。
(1)把两弹簧的一端与滑块连接,另一端固定在导轨的两端。在滑块上装上一个挡光框,待滑块静止后,将光电门放在平衡处,使挡光框正好挡住光线。
(2)将毫秒计的功能开关置 S2 挡,时间选择开关用最小的一挡。使滑块偏离平衡位置 10.0 cm(从导轨的标尺上可看出),由静止释放。滑块经过光电门时,毫秒计记下挡光时间 t,如果挡光框两前沿之间的距离为 d,则滑块经过光电门时的速度 v = \(\frac{d}{t}\)。如果滑块的质量是 m,则滑块的动能 Ek = \(\frac{1}{2}\)mv2 = \(\frac{{m{d^2}}}{{2{t^2}}}\)。
(3)改变滑块偏离平衡位置的距离 x(如 15.0 cm,20.0 cm,…),重复操作(2),得到若干组(x,Ek)值。
(4)作 Ek–x2 图,得到一条过原点的直线,就可以说明弹簧的弹性势能与它形变量的平方成正比。
4.实验验证机械能守恒定律
(1)用单摆做定量测量。装置如图 8–15 所示。在长 l 约 0.5 m 的细线下端拴一个质量为 m 的金属球,细线的上端用两片形状如图中 N 所示的木片夹牢,木片由烧瓶夹固定在铁架(图中未画出)的上部。水平木条 T 也装在铁架上部,铁架下部装一个刀片 D,刀片平面取水平方向,刀刃应与摆线的运动方向 v 斜交而不要垂直(见俯视图),这样才能迅速把线割断。仔细调整刀刃的位置,使之恰好能在球摆到最低点时把线割断,割断处应尽量靠近摆球。在水平地面上放一张白纸,上面再放一张复写纸,即图中的 E。
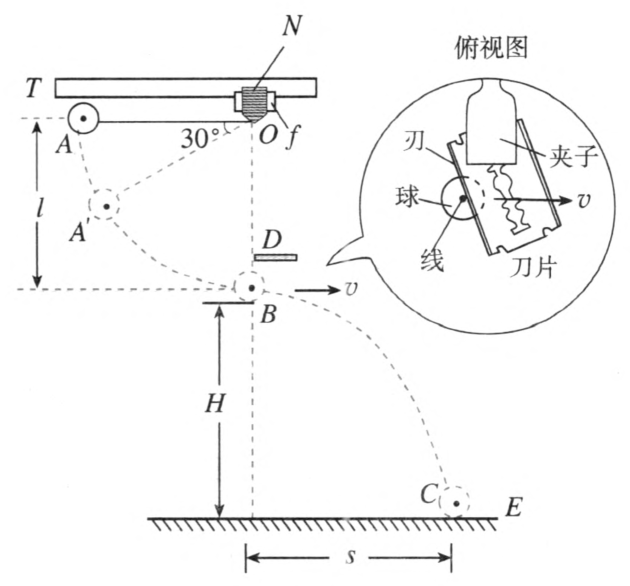
实验方法是:在摆球静止时,量出摆长 l(悬点 O 到球心距离)和球的下缘到地面的竖直高度 H。以木条 T 为基准,把摆拉成水平,自 A 点由静止开始释放。摆到最低点 B 时,线被割断,球被平抛出去,落在复写纸 E 上,打出痕迹,记录下落地点 C,再量出水平射程 s。利用平抛运动规律求出球在 B 点的速度 v = \(\frac{s}{{\sqrt {\frac{{2H}}{g}} }}\),再计算球由 A 到 B 过程中动能的增加量 ΔEk = \(\frac{1}{2}\)mv2,由 l 值计算球由 A 到 B 过程中重力势能的减少量 ΔEp = mgl,最后看 ΔEk 是否与 ΔEp 近似相等。
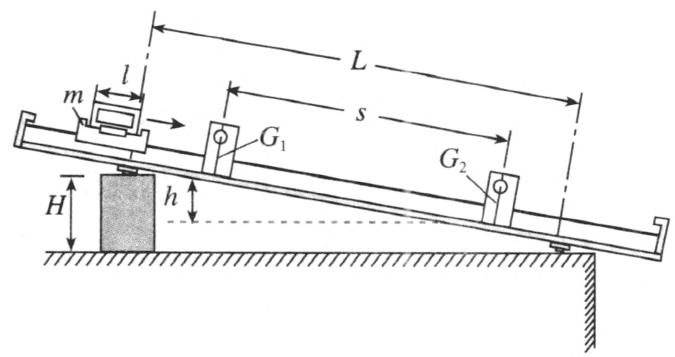
(2)用气垫导轨做实验。先仔细地把导轨调成水平,然后如图 8–16 所示用垫块把导轨的一端垫高 H。滑块 m 上面装 l = 3 cm 的挡光框,使它由轨道上端任一处滑下,测出它通过光电门 G1 和 G2 时的速度 v1 和 v2,就可算出它由 G1 到 G2 这段过程中动能的增加量 ΔEk = \(\frac{1}{2}\)m(v22 − v12)。由图可知 \(\frac{h}{s}\) = \(\frac{H}{L}\),由已知的 L 值和所取的 H、s 值可算出 h 值,再算出滑块由 G1 到 G2 这段过程中重力势能的减少量 ΔEp = mgh。由实验结果可看出 ΔEk ≈ ΔEp,从而证明机械能守恒。实验时,s 值要取得小些,可减少滑块克服阻力做的功,使结果 ΔEk 与 ΔEp 两个值更接近。
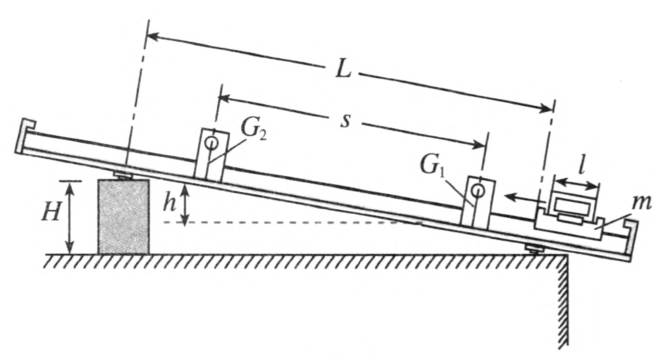
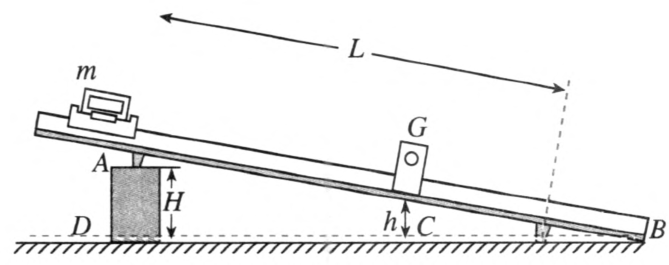
(3)也可以用相反的过程来验证,如图 8–17 所示。用轨道下端支架上的橡皮筋把滑块以足够的初速度(但不宜太大)弹出,使之沿轨道向上端运动,测定它由 G1 到 G2 过程中动能的减少量和势能的增加量,看两者是否相等,测算方法同前。也可以测算若干点的总机械能,看是否相等。方法如图 8–18 所示,令滑块 m 从轨道上端某一点 A 由静止开始下滑,重复多次,改变光电门 G 的位置 C,测出滑块到达不同点的速度 v。以轨道末端的水平面 BD 为零势能面,确定所测各点的高度 h,h = BC×\(\frac{H}{L}\)。最后计算出每一点的总机械能 E = Ek + Ep,看它们是否相等。注意要使 C 点距 A 点近一些,这样实验结果的误差较小。
发布时间:2025/7/23 下午4:28:46 阅读次数:929
