第六章 圆周运动 参考资料

1．速度方向变化的快慢

（1）怎样描述速度的方向和方向变化的快慢？

速度是矢量，一般情况下它们的方向都用表示速度的有向线段与坐标轴的夹角表示。对于平面运动可在平面上选定一轴 Ox，速度方向由速度矢量与 Ox 轴的夹角 φ 表示，φ 也称为速度的方位角，如图 6–31 所示。

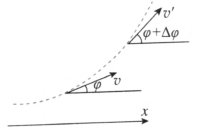
当质点做曲线运动时，速度方向时时改变，方位角亦随之改变。设 t 时刻速度为 v，方位角为 φ。t + Δt 时刻速度为 vʹ，方位角为 φʹ = φ + Δφ。方位角的改变量 Δφ = φʹ − φ 就表示速度的方向在 Δt 时间内的变化。比值 \(\frac{{\Delta \varphi }}{{\Delta t}}\) 表示方位角的变化快慢，称为速度方向的平均变化率，取此值的极限得

\[\mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \varphi }}{{\Delta t}} = \frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}}\]

它表示在 t 时刻速度方向的变化率。所以速度方向的变化快慢，由速度的方位角对时间的导数来描述。

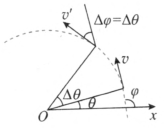
设质点作圆周运动，如图 6–32 所示建立 Ox 轴，则质点速度的方位角 φ 与角坐标 θ 之间的关系为

\[\varphi  = \theta  + \frac{\pi }{2}\]

所以有

\[\frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} = \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = \omega \]

即速度方向的变化率等于质点的角速度 ω。可见，对于圆周运动，角速度就表示了速度方向变化的快慢。

（2）向心加速度不描述速度方向变化的快慢

向心加速度 a_n = \(\frac{{{v^2}}}{r}\) = vω，即向心加速度等于速率与角速度之积。前面已指出，角速度描述速度方向变化的快慢，因而不能说向心加速度描述了速度方向变化的快慢。

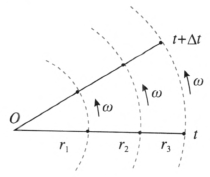
例如，有三个质点做匀速率圆周运动，它们的角速度 ω 相同，半径不同，分别为 r₁，r₂ 和r₃。由 a = vω 可知，它们的向心加速度不同。而速度方向的变化率 ω = \(\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}}\) 却相同，如图 6–33 所示。

又如两个质点作匀速率圆周运动，一个半径为 r₁，角速度为 ω₁；另一个半径为 r₂ = 4r₁，而角速度 ω₂ = \(\frac{1}{2}\)ω₁，它们的向心加速度相同，即 r₁ω₁² = r₂ω₂²。它们的速度方向的变化率之比为 2∶1。

可见，不能认为向心加速度描述了速度方向变化的快慢。

根据公式 a_n = \(\frac{{{v^2}}}{r}\) = vω，只能说，对速率相同的质点，向心加速度的大小可描述速度方向变化的快慢。

（3）怎样正确理解向心加速度的意义

向心加速度（或法向加速度）是由速度的方向变化引起的。根据定义可知

\[{a_{\rm{n}}} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\left| {\Delta v} \right|}}{{\Delta t}}\]

其中 Δv 是由于速度方向变化而引起的速度矢量的改变量，|Δv| 既与速度方向的改变量 Δθ 有关，又与速度的大小 v 有关。所以 a_n 不只是表示方向角的变化 Δθ。

根据向心加速度的定义，向心加速度或法向加速度的物理意义是：它描述了由于速度方向的变化而引起的速度矢量的变化率。

2．离心运动的应用

一池污水，若顺其自然靠重力沉降，往往需要几个月才能清浊分明。微粒的沉降，由于存在着分子热运动的干扰作用，靠重力作为推动力不仅极其缓慢有时甚至是不可能的。例如，在蔗糖水溶液中，蔗糖分子要沉降 1 mm 就需要 100 年。啤酒、果汁何以清澈透亮？如何从牛奶中提取奶油？如何将油田中喷出的油水混合液进行油水分离？如何将血液中的血细胞和血浆分开？究竟依靠的是何种推动力呢？

（1）离心分层现象

在一个盛有清水的圆筒形容器（转鼓）中，倒入一组同样大小的钢球和木球，然后启动电机使其绕轴高速旋转。此时，由于离心力的大小正比于物体的质量（在体积相同的正比于它的密度），所以钢球很快被甩到最外层，而木球则被推向转轴，清水则占据了“中间地带”（图 6–34）。可见，一旦转鼓高速转动起来，容器中的物质就会按密度分层排列。密度小者（轻相）聚集在“中央”即转轴附近，密度大者（重相）则分散在“边区”即转鼓壁附近。这种现象称为离心沉降。如果在转鼓上开满小孔，则其中的液体就会在离心力作用下通过小孔被“驱逐出境”，而固体颗粒则停留在转鼓壁面上，从而达到脱水的目的，这种现象称为离心过滤。例如，奶油的提取，啤酒、酒、果汁的澄清，污水的净化，就属于离心沉降；而煤、矿右和海盐的脱水等则属于离心过滤。

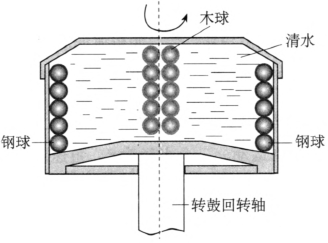
上面这个实验告诉我们，要将存在密度差的两种物体（液体或固体）高效地分离开来，可以依靠惯性离心力，它是由物体做高速转动所产生的。瑞典科学家斯维伯格和比姆斯曾使用比重力场大五万至十万倍的离心力场，高效地完成像细菌、病毒等超细微粒（直径只有万分之几乃至十万分之几毫米）的沉降，将它们从水状悬浮液中分离出来。

（2）离心分离术

啤酒何以清澈透亮？原来，这也与离心分离密切相关。在麦汁中含有一种极不稳定的冷凝固物，应尽量减少其含量才能保证成品啤酒不致出现冷混浊现象。然而这种冷凝固物的粒子极其微小，直径仅有 0.1 ~ 0.5 μm，很难除净。若采用高速离心机进行处理，就比较容易实现净化。因为这种粒子虽然极微小，但由于它与液相之间存在密度差，所以一旦进入强大的离心力场后，二者立即“分道扬镳”，从而可以很容易把冷凝固粒子剔除。

一种名叫“离心浇铸”的先进技术，也得益于这种分离术。当模具绕一固定轴旋转达到 500 r/min 时，将熔化了的金属倒入其中，夹杂在液态金属里的气体和熔渣，由于其密度远小于液态金属，因此它们将从金属里被分离出来跑向模具的空处。按此法浇铸出的金属零件密实、均匀，可以大大提高使用寿命。

3．高速转动物体的极限转速

转动物体内各媒质元都做圆周运动，因而都需要向心力。这些向心力由它与周围媒质元的相互作用提供。因此，在转动物体内形成一种因转动而产生的应力。当转速过高时，物体会因应力过大而断裂。那么，高速转动的物体断裂前的极限转速是多大呢？

设一个半径为 R、厚度为 a、密度为 ρ 的匀质圆盘，以角速度 ω 绕过盘心的固定轴转动。在圆盘上任取一半径为 r（r < R），宽度为 dr 的细圆环（见图 6–35），由对称性知，环上各处应力相同。在环上再任取一小段 dl，其质量为 dm，dl 所对应的张角为 dθ。可以看出，dl = rdθ。而且

\[{\rm{d}}m = \rho a{\rm{d}}l{\rm{d}}r = \rho ar{\rm{d}}r{\rm{d}}\theta \]

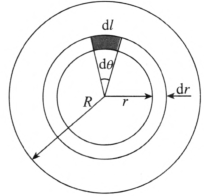
它所受到的向心力为

\[F = {\omega ^2}rdm = \rho a{r^2}{\omega ^2}{\rm{d}}r{\rm{d}}\theta \tag{1}\label{1}\]

而其他媒质元对它的作用应力 F_T 可看作是沿切线且方向相反的一对力（见图 6–36）。从几何关系可以看出，这对力产生的合力 F 指向圆心，大小为

\[F = 2{F_{\rm{T}}}\sin \left( {\frac{\theta }{2}} \right) = \rho a{r^2}{\omega ^2}{\rm{d}}r{\rm{d}}\theta \tag{2}\label{2}\]

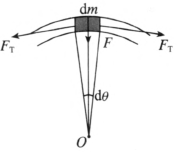
当 dθ 足够小时，sin(\({\frac{{{\rm{d}}\theta }}{2}}\)) ≈ \({\frac{{{\rm{d}}\theta }}{2}}\)。联立求解式（1）与式（2）得切应力为

\[{F_{\rm{T}}} = \rho a{r^2}{\omega ^2}{\rm{d}}r\]

又因为 ω = 2πn（n 为转速），则

\[{F_{\rm{T}}} = 4{\pi ^2}{n^2}\rho a{r^2}{\rm{d}}r\]

可见 F_T 与 r² 成正比，应力最大处应在圆盘边缘，即最大切应力为

\[{F_{{\rm{T}}\max }} = 4{\pi ^2}{n^2}\rho a{R^2}{\rm{d}}r\]

对于一根棒（或杆）来说，若对其施以拉力 F_T，则 F_T 与棒的截面积 A 之比称为抗张强度。当拉力与截面积之比超过某一临界值时，棒就会断裂。这个临界值 S 称为极限抗张强度，所以转动物体的极限抗张强度 S 为

\[S = \frac{{{F_{{\rm{T}}\max }}}}{{a{\rm{d}}r}} = \frac{{4{\pi ^2}{n^2}\rho a{R^2}{\rm{d}}r}}{{a{\rm{d}}r}} = 4{\pi ^2}{n^2}\rho {R^2}\tag{3}\label{3}\]

由式（3）解得极限转速 n_max 为

\[{n_{\max }} = \frac{1}{{2\pi R}}\sqrt {\frac{S}{\rho }} \tag{4}\label{4}\]

例如，某砂轮的外径 D 为 400 mm、安全工作线速度 v 为 50 m·s⁻¹。根据线速度与转速的关系，可以求出安全工作转速 n 为

\[n = \frac{{60v}}{{2\pi R}} = \frac{{60v}}{{\pi D}} = 2\;389\;{\rm{r}} \cdot {\rm{min} ^{ - 1}}\]

这种砂轮的极限抗张强度 S 约为 1.50×10⁷ N·m⁻²，密度 ρ 约为 2.5×10³ kg·m⁻³。由式（4）知它的极限转速 n_max 为

\[{n_{\max }} = \frac{1}{{\pi D}}\sqrt {\frac{S}{\rho }}  = 61.7\;{\rm{r}} \cdot {{\rm{s}}^{ - 1}} = 3\;700\;{\rm{r}} \cdot {\rm{min} ^{ - 1}}\]

为了保证砂轮在高速磨削过程中有足够的强度不破裂，出厂前应按安全工作转速的 1.5 倍进行检测。

4．匀速率圆周运动的向心力、频率和半径

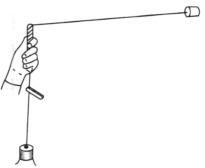
选一根圆珠笔杆，取一根 2.5 m 长的尼龙丝，一端系一个橡胶塞（或小沙袋）；另一端穿过圆珠笔杆，然后吊上 6 个 1 cm 外径的铁垫圈或两个 M10 的螺母，最后再在尾端打一死结。用一枚曲别针穿过死结，作为防止垫圈滑脱的阻挡物，见图 6–37。调节尼龙丝，使橡胶塞距圆珠笔杆的顶口（笔尖部）的线长为 1 m。握住圆珠笔杆，并在头的上方尽量使橡胶塞在一个水平面内做匀速圆周运动。此时垫圈或螺母的重力成为橡胶塞圆周运动的向心力。为了检查转动是否平稳，可用一个鳄鱼夹夹在圆珠笔杆下口的线上。记录垫圈的个数和使橡胶塞保持匀速转动的频率。调节水平部分线的长度，使旋转半径先增加 \(\frac{1}{2}\) 倍，然后再减小 \(\frac{1}{2}\)，分别数出使橡胶塞仍能做匀速转动的频率。看频率的增减与旋转半径的变化相同还是相反？是否成正比？取下曲别针，先后增加垫圈的数量至最初的 1.5 倍和 2 倍（这相当于增大了向心力），保持初态的半径 1 m，分别数出橡胶塞匀速转动的频率，看向心力如何影响转动的频率。

5．用圆锥摆验证向心力的表达式

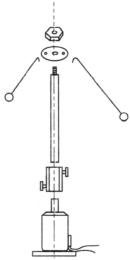
用电动机做一个电动的圆锥摆，可以改变摆长、转速以及小球的质量，做到转速稳定、半径不变、摆角 θ 不变。

选用 220 V 交直流电动机（有电刷），如图 6–38 所示，加长转轴，加长轴的端部有螺杆和螺母，用薄铁片做一个圆片中间打一个圆孔套在轴杆的螺杆上，两侧各打一个小孔做悬挂小球的支架。用直径 1 mm 左右的铁丝穿过小球做成图中所示的形状，选择不同的长度和不同的小球可以完成不同半径、不同质量的实验。电动机选择不同的低压直流电压，并且用滑动变阻器调速，可获得不同的转速，以改变小球的线速度与角速度。在转动的小球下方靠近轴的位置水平放置一根刻度尺，可以确定摆角。

6．拱形桥、凹形桥的压力实验

用 3 mm 的粗铁丝做成如图 6–39 所示的凹形桥和拱形桥，两个桥的宽度由所用的钢球直径而定，为 2 ~ 3 cm，小于钢球直径。钢球直径选择在 3 ~ 4 cm、质量在 200 g 左右。

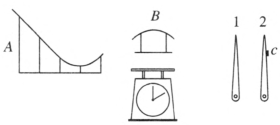
将弹簧台秤（测力计）的玻璃卸下，再卸下指针。把图 6–39 薄铁片剪成指针的形状，侧面留出一小块铁皮 c 如图中 2 所示，向上弯折与指针垂直，作为记忆指针，记忆指针的轴孔略大于原指针 1。将记忆指针安装在原指针的下面。

实验时先将拱形桥 B 用夹子固定在台秤上，记下示数，再将钢球放在台秤上，记下示数，将记忆指针推回指针 1 的位置。将凹形桥 A 安装在铁架台上，并使出口弧线与拱形桥 B 的入口弧线相切，留 2 ~ 3 mm 的间隙，钢球从 A 的某处释放，并能从拱形桥 B 上通过。当钢球从拱形桥 B 通过后，可以看到记忆指针的位置小于钢球静止放在台秤上的示数。改变钢球在凹形桥上的高度，台秤失重的示数也会改变。

将凹形桥固定在台秤上，让钢球从某处开始滚下，可以看出记忆指针的位置所指示的示数大于钢球静止时的示数。改变钢球的高度，超重的数值也会改变。

发布时间：2025/7/15 下午3:09:21  阅读次数：587