第五章 抛体运动 参考资料

1．相对运动与运动的合成

我们知道，如果物体在静止参考系 K 中的速度叫绝对速度 v_绝对，物体在运动参考系 K′ 中的速度叫相对速度 v_相对，运动参考系 K′ 相对静止参考系 K 的速度叫作牵连速度 v_牵连，则有

v_绝对 = v_相对 + v_牵连

v_相对 = v_绝对 − v_牵连

如果把这个方法应用到小船过河的问题中，则有

v_船对地 = v_船对水 + v_水对地                                                   （1）

其中，v_船对地 为船相对地面的速度，v_船对水 为船相对水的速度，v_水对地 为水流的速度。

我们研究抛体运动时，常把它看成 x 方向和 y 方向两个分运动的合运动，从速度看就是

v = v_xi + v_yj                                                                      （2）

看起来，式子（1）与式子（2）形式上相近。都是速度的合成公式，但实质上它们之间还是有区别的。（1）式是不同参考系间的速度变换关系，而（2）式是同一参考系中的速度合成关系。它们的含义不同，适用范围也不同。（2）式是在同一个参考系中由矢量运算得到的，在速度很小到速度很大（大到接近光速）的范围内仍然成立。（1）式由伽利略变换导出，因而只在低速时（远小于光速）才成立。

从狭义相对论可以知道，不同惯性参考系之间的速度变换公式为

v = $\frac{v^{\prime }+u}{1+\frac{v^{\prime }u}{c^2}}$                                                                     （3）

或                                                             vʹ = $\frac{v+u}{1-\frac{vu}{c^2}}$

其中 v 为质点在惯性参考系 K 中的速度，该质点在另一惯性参考系 Kʹ 中的速度为 vʹ，Kʹ 系相对 K 系的速度为 u，c 为光速。v、vʹ、u 都沿同一直线同方向运动。

当运动速度远小于光速时，（3）式就变为

v = vʹ + u                                                                          （4）

或                                                                                       vʹ = v − u

参考系问题是物理学中的基本问题，教师应该特别重视。由于初学者学习相对运动问题有一定的困难，现行高中教材一般不去区分它们之间的区别。

2．流体介质阻力对物体运动的影响

我们知道，抛射体在真空中的飞行轨迹是一条抛物线。假定弹丸的初速度为 850 m/s，发射角为 43°，则弹丸在真空中的射程等于 73 km，而当考虑空气阻力时，弹丸的射程只有 8 km 左右，仅为理想射程的 $\frac{1}{2}$（图 5–31）。

大量实验表明，当物体在空气中的飞行速度 v < 0.2 m/s 时，阻力 F = kv；当 0.2 m/s < v < 240 m/s 时，F = kv²；当 240 m/s < v < 450 m/s 时，，F = kv³。其中比例系数 k 反映了除物体速度以外的其他诸因素对介质阻力的影响。考虑空气阻力时弹丸的飞行轨迹如图 5-32 所示。容易看出，当考虑空气阻力时，弹丸的落地角 β 大于发射角 α（在真空中落地角β 等于发射角 α），而且落地角接近 90°。

理论计算和实际观察都已证明，物体在空气中运动一段较长时间后，将几乎竖直向下匀速降落，并趋近于它的极限速度。所谓极限速度是，在介质阻力的影响因素已经确定的情况下，物体在介质中运动需经无限长的时间才能达到的速度。在许多实际问题中，如选矿、选种和清洁谷粒等，常利用物体极限速度的不同把不同的颗粒分开。

跳伞运动员自飞行器中跳出后，如果不张开伞，则阻力系数较小，极限速度一般可达到50 ~ 60 m/s。以这个速度落地，任何人也承受不了。但如果张开伞，则阻力系数变大，极限速度一般不超过 4 ~ 5 m/s。这个速度仅相当于我们从 1 m 多高的矮墙上跳下时按自由落体的速度公式计算所得到的落地速度。这对于普通健康的人来说，是没有危险的。战争中对伞兵的要求不仅是能安全落地，而且在空中停留的时间越短越好。为此伞兵在刚跳离飞行器后，可先不张伞，等降至一定高度后再把伞张开。

3．地球自转对抛射体的影响

实际上，在计算落地点时，不但要考虑空气阻力的影响，还要考虑地球自转的影响。

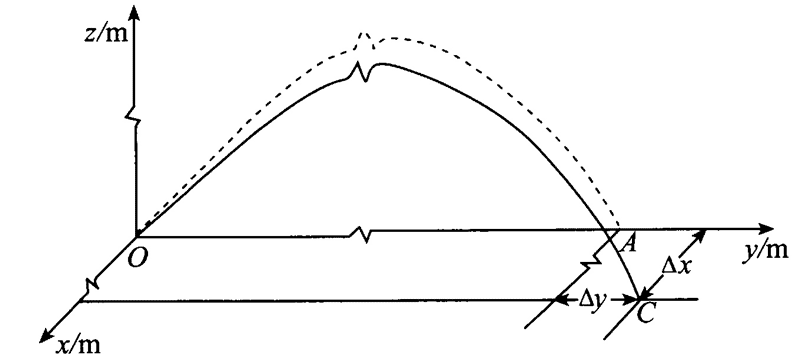
当考虑地球自转的影响时，抛射体还将受到科氏惯性力的作用，其飞行轨迹则不再是一条平面曲线，而是一条空间曲线了。所谓科氏惯性力，它是在考虑地球自转这样的非惯性参考系中应用牛顿第二定律时，必须附加在物体上的一项作用力，否则，物体的质量 m，加速度 a 与作用力 F 之间的关系式 F = ma 不成立。实际上，即使不考虑地心每年绕太阳一周的公转运动，地球也还有每昼夜绕地轴转一周的自转运动（自转角速度为 7.29×10⁻⁵ rad/s）。假如在北半球纬度为 45° 处，向正东方向以发射角43°，初速度 850 m/s 发射炮弹，当不考虑地球自转的影响时，炮弹在真空中的飞行轨迹如图 5-33 中的虚线所示，落地点为 A；当考虑地球自转的影响时，炮弹在真空中飞行的轨迹如图 5-33 中的实线所示，落地点为 C。与不考虑地球自转时相比，炮弹在真空中飞行的落地点向东偏移的距离 Δy 约为 338 m，向南偏移的距离 Δx 约为 454 m。一般普通炮弹的爆炸威力范围只有几十米，因此地球自转对抛射体落地点的影响也应该引起重视。

4．利用平抛分解演示仪研究平抛运动

如图 5–34 所示，上部分水平并列地固定相同弧形的两条轨道 A 与 B，轨道左端分别安装一个电磁铁 C 与 D，用于释放钢球。轨道 A 出口的水平部分较短，出口处安装触发开关 O，控制出口处电磁铁 F 电源的通断。轨道 B 的水平部分上安装有一个可自由左右移动的装置 E，用于捕捉及定位该轨道上的运动球。从轨道 A 释放的钢球做平抛运动，从轨道 B 释放的钢球做匀速直线运动，从电磁铁 F 释放的钢球做自由落体运动。

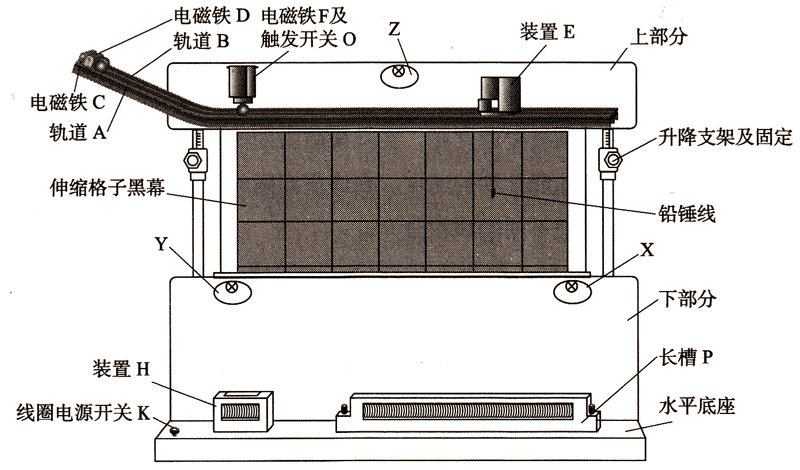
装置下部分安装一个捕捉及定位平抛运动球的长槽 P，以及一个接收竖直方向上自由落体运动球的装置 H。长槽 P、装置 H 及装置 E 分别安装捕提触发器，当受到钢球撞击时可以使相应的运动指示灯 X、Y、Z 发光。再安装三组时间显示器与刻度尺，分别用来测量三个球的运动时间及对应的位移。

利用上述装置可定性观察及定量探究平抛运动在整直方向、水平方向上的分运动特点。

（1）把两个钢球分别吸在电磁铁 C 与 F 上，并确保电磁铁F的钢球与轨道 A 的出口处于同一高度。释放轨道 A 的钢球，到出口处使电磁铁 F 断电，释放钢球。观察对比两球运动指示灯 X、Y 是否同时发光。

（2）平抛运动球被捕捉定位后，用一根铅垂线在轨道 B 上找到对应位置，将装置 E 移到该位置。

（3）三个钢球分别吸在电磁铁 C、D 与 F 处，电磁铁 D、C 与在步骤（1）中的高度相同，断开线圈电源开关 K，使 C、D 两钢球以同样的初速度同时水平射出。

（4）观察对比运动指示灯 X、Y、Z 是否同时发光，并获得一组实验数据。

（5）通过升降支架可改变高度，也可改变电磁铁 C、D 在轨道上的相对高度，重复上述步骤可得多组实验数据。

发布时间：2025/6/21 下午8:01:11  阅读次数：355