第四章 运动和力的关系 参考资料
1．牛顿运动定律的建立
牛顿在 1687 年出版的《自然哲学的数学原理》（以后简称《原理》）一书中，发表了运动三定律。它的诞生是在前人工作的基础上，以培根的实验哲学为思想指导，用伽利略开创的实验与数学分析结合的方法建立起来的。
（1）历史给牛顿提供的基础
对牛顿力学的建立直接提供基础的主要有以下几位先驱的成就。
①伽利略是近代科学的奠基者。他开创了科学的实验方法，他在科学方法论以及运动学、动力学方面的成就，都对牛顿运动定律的发现有直接的影响。伽利略在力学方面的主要贡献如下。
对运动的定量描述。伽利略第一个用数学的方法来分析运动。他定义了匀速运动，把匀速引伸到变速，把平均速度引向瞬时速度，用速度对时间的变化定义加速度这一重要概念。伽利略决定采用以时间作为运动学的基本变量，研究位置、速度随时间变化的规律。这一点不仅对牛顿，甚至对以后物理学的发展都起到十分重要的作用。
对自由落体运动的研究。伽利略为了“冲淡重力”，用斜面做实验，结合数学分析，总结出斜面运动是匀加速运动，其规律为 x = 。他运用科学推理将斜面的倾角逐渐增大到90°，从而得到自由落体的运动规律。
提出运动叠加原理，研究抛体运动。伽利略仔细地研究了抛体运动规律，并发现了运动叠加原理，即一个运动可以看成由几个各自独立进行的运动叠加而成。他计算了抛射仰角从 0 到 90° 的各种角度时的射程。用实验结合数学证明了 θ = 45° 时射程最大，θ = 45° ± α 时有相同的射程等结论。
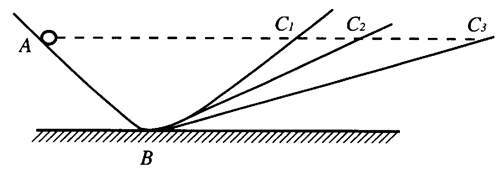
惯性定律方面的工作。伽利略通过对接斜面的实验（图 4–10），发现小球从 AB 斜面滚下将沿斜面 BC 升到同样的高度。如果将斜面 BC 平放，则小球沿 BC 斜面运动的长度将增加。进而他提出了“理想实验”并得出结论：如果使 BC 斜面变成水平，则运动将继续下去而不需要外力来维持。于是他提出“任何速度一旦施加给一个运动着的物体，只要除去加速或减速的外因，此速度就可保持不变，不过这是只能在水平面上发生的一种情形。”这一发现接近于牛顿惯性定律。但是，伽利略的表述中有明确的“圆惯性”的烙印，他指的匀速运动是沿与地心等距的水平面运动。并且伽利略把重力看作物体内在的属性，把它排除在外力之列。
提出相对性原理。伽利略阐明了运动和静止的相对性，并指出了互做匀速直线运动的不同参考系，在描述运动规律方面等价这一重要原理。
②笛卡儿是法国自然哲学的代表人物，他在古代演绎法基础上创立了数学演绎法，主张以唯理主义为根据，从简单自明的直观公理出发运用数学逻辑推出结论。他把当时占统治地位的几何思维用代数思维加以简化，从而创立了解析几何学。笛卡儿的数学演绎法和弗朗西斯·培根的实验归纳法一起，成为近代物理学方法论的两大源泉。笛卡儿在力学上的具体成果如下。
纠正了伽利略惯性表述中圆惯性的缺陷。提出“如果物体处在运动之中，那么如无其他原因作用的话，它将继续以同一速度在同一直线方向上运动，既不停下，也不偏离原来的方向”。牛顿的惯性定律直接继承了笛卡儿的这一发现。
从他的哲学原则出发提出了运动守恒的思想。他初步形成动量（运动量）的概念，认为运动量等于物体的大小和速度的乘积（没有质量概念），并应用“运动量”守恒来研究碰撞。但是，笛卡儿没有给运动量赋予矢量性。并且，他不了解碰撞中弹性与非弹性的区别，所以他的碰撞定律多数是不正确的。
③惠更斯是荷兰物理学家、天文学家和数学家。他最初是笛卡儿自然哲学的追随者，但他在范围很广的实验技术研究和理论研究中，采取了实验归纳与数学演绎相结合的方法，作出了很突出的成就。他在力学方面的主要贡献如下。
发展并完善笛卡儿的运动量守恒原理，给笛卡儿的运动量加上方向性，使之成为矢量。研究了弹性碰撞，指出在这类碰撞中除运动量守恒外，活力也守恒（即 ∑imivi2 不变）。
对摆进行研究（实验和理论），求出了单摆的周期公式。
引入圆周运动的向心加速度概念，导出向心加速度的公式。
（2）牛顿的伟大综合
17 世纪后半叶，牛顿所处的时代随着生产技术的发展，对天上地下的物体运动规律积累了许多研究成果，并与之相联系初步形成了科学方法论。从力学发展来看，在已有的基础上，把各个零散的实验事实、概念和规律加以总结，而形成统一的力学体系的条件已经具备。牛顿以实验为依据、以数学推理为方法，从对运动的研究中创立了微积分（牛顿称之为流数术），从而用统一的观点解决天上行星和地面物体的力学规律，并在这一过程中，总结出三个运动定律和万有引力定律。牛顿在总结三大定律方面作出了如下独特贡献。
①明确定义了惯性这一概念，指出惯性是物体固有的对改变运动状态的抵抗能力。并且定义了质量，指出惯性与质量成正比。在这个基础上，采用了笛卡儿的表述作为他的第一条运动定律，即惯性定律。
②明确定义了力这个重要概念。在牛顿以前关于力的概念是混乱的，牛顿首先把力限制为物体间相互作用的自然力，是改变物体运动的外因。而且，发现了牛顿第三定律这一重要的定律。
③明确定义动量、建立运动定律。在笛卡儿与惠更斯的基础上，明确了动量（即运动量）的定义是质量与速度的乘积。并通过对实验现象的归纳，总结出动量变化与外加力之间的定量关系，即牛顿第二定律。
④区别重量和质量，改变了伽利略认为重力是“物体同有的力”这种看法。指出重力是地球对物体的引力，并根据惠更斯的单摆周期公式进行大量的实验，总结出重力与质量成正比这一结论。
⑤在《原理》中，在三条运动定律之后的六条推论中包括了力的平行四边形定则、动量守恒、质心运动、相对性原理、力系的等效原理等。论述了碰撞问题，提出了非弹性碰撞的恢复系数，牛顿公式等。所有这些，连同对天上地上运动问题的解决，使三大定律立即显示出巨大的魅力，成为粗具规模的力学体系。
2．牛顿第一定律的意义
牛顿第一定律是通过从伽利略、笛卡儿到牛顿的几位杰出科学家的努力总结出来的自然定律，它否定了几千年来人们关于运动和力的错误观念。通过对不受力作用的物体的运动状态的描述，揭示出周围环境对物体施加的作用力是物体运动状态变化的原因。只有在此基础上才有可能进一步研究受力作用的物体运动变化的规律。所以牛顿第一定律的建立，在观念上是革命性的变革，在科学的动力学体系中是不可缺少的重要基础。
可以从以下几个方面深入理解牛顿第一定律的丰富内涵和它的重要意义。
（1）提出了力的定性定义
牛顿第一定律通过对不受力的物体的运动状态的描述，绐出了力的定性定义。牛顿在牛顿第一定律前的定义中明确提出：力是物体对物体的作用，使物体改变静止或匀速直线运动状态。这就对力的概念给出了定性的、科学的定义。其要点之一是力的起源：力是物体对物体的作用。力存在于这种作用过程之中。其要点之二是，力的作用效果：使受力物体的运动状态发生变化，即产生加速度。
在运动定律方面牛顿超过伽利略的重要方面之一，就在于科学地定义了力这个重要概念。它使原来关于推力、拉力这种模糊认识上升到科学概念，从而大大拓宽了人们对力的认识，拓宽了力的范围。
（2）惯性概念的确立
牛顿第一定律表明：每一个物体都具有保持静止或沿一直线做匀速运动状态的属性，这就是惯性。牛顿在第一定律前的定义中，明确定义了“惯性”这一概念。他指出：“惯性是一种起抵抗作用的能力。它存在于每一个物体当中。”这种抵抗作用的能力，“使之保持其现有状态，或是静止，或是匀速直线运动。”显然，这里所说的起抵抗作用的能力，是指对外界改变物体运动状态的作用的抵抗能力。
因此，惯性是物体固有的属性，是不论物体是否受力都具有的性质。当物体没有受外力作用时，静者恒静，动者恒做匀速直线运动，是物体惯性的表现；当物体受到外力作用时，杨体的惯性表现于对外界作用的“抵抗性”（此即牛顿所说“抵抗能力”的含意）。这种“抵抗性”在牛顿第二定律中将得到进一步的定量的阐明。
（3）定义了惯性系
参考系是描述物体运动的依据，人们可以任意选定一个参考系来对物体的运动进行描述。对任何物体，不管它是否受力，都可以找到一个参考系，在此参考系中，该物体是静止或做匀速直线运动的。可见，离开参考系谈惯性定律是毫无意义的。
牛顿第一定律把“不受其他物体作用”作为“物体继续保持静止或匀速直线运动”的条件，就界定了牛顿力学适用于一类特殊的参考系，这类特殊的参考系就是不受力作用的物体在其中静止或做匀速直线运动的参考系，称为惯性参考系。牛顿第一定律正是通过不受外界作用的物体的运动状态来定义惯性参考系，从而使它成为整个力学甚至物理学的出发点。
（4）在力和运动的关系方面观念上的突破
从亚里士多德以来近两千年中，人们相信运动是由力维持的。牛顿第一定律否定了这种根深蒂固的偏见，通过对不受力作用的物体运动规律的描述，揭示出力是运动变化的原因。科学的力学只有首先明确不受作用的物体是怎样的运动，才有可能弄清受力物体运动变化的规律。所以，牛顿第一定律扫清了关于运动和力的关系在认识上的障碍，成为动力学的基础。
可见，牛顿第一定律的确是作为牛顿力学体系出发点的一条规律，它具有特殊意义，是三大定律中缺一不可的独立定律。如果把它作为牛顿第二定律的特殊情况，就大大地贬低了牛顿第一定律的意义与作用。如果进而将牛顿第一定律的“无外力作用”修改为“合外力为 0”，就更不妥当了。合外力为 0 时加速度为 0，与牛顿第一定律所说的物体在无外力作用时的运动规律相同，这只能说明牛顿第一定律和牛顿第二定律之间是相互协调的。
3．通过可操作性定义认识牛顿第二定律
牛顿第二定律是牛顿力学中十分重要的内容，它确立了力、质量和加速度三者之间的定量关系。那么，牛顿第二定律究竟是实验定律还是力和质量的定义呢？
从力学发展的历史看，牛顿运动定律是在静力学和动力学方面已有的基础上，首先引入了物体之间相互作用的力和质量的概念，然后通过实验归纳法总结出来的。这类作为学科基础的实验定律，在建立时可能在逻辑上不够严密，但它总是在当时的水平上反映了人们的实践经验。对于力和质量也可以采用某种量度方法，如根据力使物体变形的效应来量度力，根据质量与重量成正比的判断来量度质量等。这种量度的根据可能与定律本身在逻辑体系上不够协调，但是一经建立了规律，也就同时为严格量度这些量提供了依据，并可以反过来审查原来的那种量度的准确程度和适用范围。所以，把牛顿运动定律作为用实验归纳法总结出的基本定律直接加以介绍，不追究力和质量的量度，或把它作为在实际上已经解决了的问题，把主要精力用在讲清定律的意义，仍不失为讲解牛顿运动定律的一种方案。
然而，在 19 世纪下半叶，以奥地利物理学家马赫为代表的一些学者，用批判的态度审查了牛顿力学的基础，同时也指出牛顿第二定律在逻辑上存在问题：牛顿第一定律中并不涉及力和质量的定量量度，而牛顿第二定律把两个未经定量定义的量——力和质量联系起来。
在这种情况下，人们考虑：怎样既采纳马赫的主张，对任何物理量都有确切的定义，并能在相互协调的逻辑体系内按一定的操作程序用明确的可测量来进行量度；同时，又能保持牛顿运动定律作为基本的实验定律的地位。于是，出现了另一种在逻辑上能自洽的说法，通过对力和质量提供一种可操作性的定义来讨论牛顿第二定律。
我们可以通过图 4–11 甲所示的实验装置研究力和加速度的关系。在水平的光滑平面上放一个底面光滑的重物 A0（我们称它为标准物体）。从图中可以看到，实验中可以通过重物下面的一个白色小三角确定它的位置。另一个重物 B 放置在与水平桌面相接的斜面上，A0 与 B 之间用跨过滑轮的细线连接，用 B 来牵引 A0，使之产生一定的加速度。在细线中间接入一个弹簧，以其伸长量 Δl 来记录牵引力的大小。（由于力还没有定义，此时接入的弹簧还不是一个“弹簧测力计”，与弹簧一端固联的小牌上没有刻度来标示力的大小。）
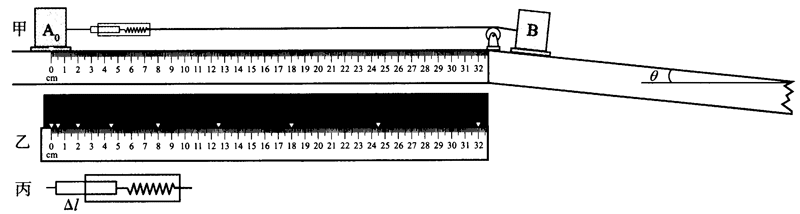
做实验时，A0 以桌面标尺的零点为初始位置从静止出发，以后每经过固定时间间隔（如 0.1 s）的位置用频闪摄影记录，用以算出它的加速度。与此同时，我们监视弹簧伸长量 Δl 有无变化。图 4–11乙所示是 A0 位置的频闪摄影，它所显示的读数标记在标尺上。A0 是否做匀加速运动，可由位移 x 是否与 t2 成正比来检验。如果 A0 做匀加速运动，则加速度以可由公式 x =
通过实验，对于标准物体 A0 我们得到以下一些结果：
（1）沿斜面下滑物体 B 的牵引力是恒力，在恒力作用下 A0 做匀加速运动。
（2）改变牵引的情况（如把牵引物 B 换大一些或小一些，或把斜面的坡度 θ 调小一些或大一些），如果每次使得弹簧的伸长量 Δl 一样，则 A0 的加速度 a 一样。反之，当弹簧的伸长量 Δl 不同时，则 A0 的加速度 a 也不同。
在通常的情况下，可以认为弹簧的一定伸长量对应一定大小的力，所以上述实验表明：恒力产生恒加速度，力的大小与 A0 加速度的大小是一一对应的。
这里产生了一个如何规定力大小的问题：应该认为力的大小正比于弹簧的伸长量呢，还是正比于加速度的大小呢？这不是实验的问题，而是定义的问题，或者说是约定的问题。按照惯性原理的精神，力是产生加速度的原因，我们应当采取后者。也就是说，应当用加速度的大小作为力的量度来标度弹簧的伸长量。
具体地说，与弹簧一端固连的小牌本是空白的，其上原无刻度。如果在弹簧伸长量为 Δl1 时标准物体 A0 的加速度为一个单位（如 a = 1.0 m/s2），我们就在小牌上该处作个标记，注上“1”，表示弹簧伸长到这里时对应着力的大小等于一个单位；在弹簧伸长量为 Δl2 时标准物体 A0 的加速度为二个单位（譬如 a = 2.0 m/s2），我们就在小牌上该处作个标记，注上“2”，表示弹簧伸长到这里时对应着力的大小等于二个单位；在弹簧伸长量为 Δl3 时标准物体 A0 的加速度为三个单位（譬如 a = 3.0 m/s2），我们就在小牌上该处作个标记，注上“3”，表示弹簧伸长到这里时对应着力的大小等于三个单位，等等。于是我们就得到了一个初步有了刻度的弹簧测力计。
到现在我们测力计的标尺上只有少数几个整数标记 1，2，3，…非整数，如 2.5 个单位的力应该标在什么地方呢？可以取标尺上 2 到 3 之间的中点吗？不行，我们不能先验地知道，弹簧伸长量的中值一定会产生加速度的中值（亦即按定义对应着力的中值）。实验必须再做下去。调整斜面的坡度，使 A0 的加速度达到 2.5 m/s2，然后在测力计的标尺上相应的地方做出 2.5 个单位力的标记。这样的实验继续下去，直到测力计的标尺上有了足够密的标记。标记之间的空隙再用内插法来弥补，我们就得到了一个定了标的弹簧测力计。
现在我们可以明确下面两个说法：
1．使标准物体 A0 产生同样加速度的力大小相等。
2．使标准物体 A0 产生 n 倍加速度的力也是 n 倍。
也就是说，对于标准物体 F ∝ a。
应当强调，这个关系是如何标定力的大小的约定，不是定律。
在上面的讨论中我们始终局限于标准物体，现在我们要扩展到任意物体了。我们设想，把标准物体 A0 换成任意其他物体 A1、A2、…重做上述所有实验。结果表明：
（1）使任意物体产生同样加速度的力大小是相等的。
（2）使任意物体产生 n 倍加速度的力也是 n 倍。
这里使用的测力计是由上述标准物体来标度的。于是我们得到对于任意物体都有 F ∝ a。此时，这个结论已经是一条广泛的实验定律了。
我们已经看到，对于任意一个物体，力 F 与加速度 a 成正比。写成等式，则有 F = a。对于同一物体比例系数 m 是个常量；对于不同物体，比例系数 m 一般不同。在同样大小的力的作用下，不同物体产生的加速度 a 反比于 m，有 a =
所以，比例系数 m 反映了一个物体运动状态（速度）改变的难易程度：当受到同一个力时，m 大的物体加速度小，运动状态难以改变；m 小的物体加速度大，运动状态易于改变。我们把物体保持运动状态不变的性质叫“惯性”，m 大表示物体的惯性大，m 小表示物体的惯性小，m 称为物体的惯性质量，有时简称质量。
为了得到国际上规定的力的单位，我们应选取 A0 为质量 m0 = 1 kg 的物体。这样一来，用 A0 的加速度定标的测力计所定的力的单位就应该是 kg·m/s2，这个单位有个专门名称，叫作牛顿，符号 N。通过上面的讨论，我们就可以得到一个逻辑上严格和自洽的牛顿力学的体系了。
4．理想实验及其在科学研究中的作用
所谓“理想实验”，又叫作“假想实验”“抽象的实验”或“思想上的实验”，它是人们在思想中塑造的理想过程，是一种逻辑推理的思维过程和理论研究的重要方法。
“理想实验”虽然也叫作“实验”，但它同真实的科学实验是有原则区别的，真实的科学实验是一种实践的活动，而“理想实验”则是一种思维的活动；前者是可以将设计通过物化过程而实现的实验。后者则是由人们在抽象思维中设想出来而实际上无法做到的“实验”。
但是，“理想实验”并不是脱离实际的主观臆想。首先，“理想实验”是以实践为基础的。所谓的“理想实验”就是在真实的科学实验的基础上，抓住主要矛盾，忽略次要矛盾，对实际过程作出更深入一层的抽象分析。其次，“理想实验”的推理过程，是以一定的逻辑法则为根据的，而这些逻辑法则，都是从长期的实践中总结出来的，并为实践所证实了的。
在自然科学的理论研究中，“理想实验”具有重要的作用。作为一种抽象思维的方法，“理想实验”可以使人们对实际的科学实验有更深刻的理解，可以进一步揭示出客观现象和过程之间内在的逻辑联系，并由此得出重要的结论。
例如，作为经典力学基础的惯性定律，就是“理想实验”的一个重要结论。这个结论是不能直接从实验中得出的。伽利略通过实验发现，当一个球从一个斜面上滚下而又滚上第二个斜面时，球在第二个斜面上所达到的高度同它在第一个斜面上开始滚下时的高度几乎相等。伽利略断定高度上的这一微小差别是由于摩擦而产生的，如能将摩擦完全消除的话，高度将恰好相等。然后他推想，在完全没有摩擦的情况下，不管第二个斜面的倾斜度多么小，球在第二个斜面上总要达到相同的高度。最后，如果第二个斜面的倾斜度完全消除了，那么球从第一个斜面上滚下来之后，将以恒定的速度在无限长的平面上永远不停地运动下去。这个实验是无法实现的，因为永远也无法将摩擦完全消除掉。所以，这只是一个“理想实验”。但是，伽利略由此而得到的结论，却打破了自亚里士多德以来两千多年间关于受力运动的物体，当外力停止作用时便归于静止的陈旧观念，为近代力学的建立奠定了基础。
除此以外，爱因斯坦在建立狭义相对论时，曾经做了关于同时性的相对性的一个“理想实验”，从而了提出同时的相对性。而在建立广义相对论时，他又通过自由下落的升降机的“理想实验”，揭露了引力质量和惯性质量的相等。量子论的建立中，海森堡用来推导测不准关系的电子束的单缝衍射实验，也是一种“理想实验”。
因此可以看出，“理想实验”在自然科学的理论研究中有着重要的作用。但是，“理想实验”的方法也有其一定的局限性。“理想实验”只是一种逻辑推理的思维过程，它的作用只限于逻辑上的证明与反驳，而不能用来作为检验认识正确与否的标准。相反，由“理想实验”所得出的任何推论，都必须由观察或实验的结果来检验。
5．惯性力与失重
在非惯性系中，如果想让牛顿第二定律依然在形式上成立，就需要引入惯性力的概念。惯性力不是因相互作用而产生的，而是人为认为它存在的力，可以说它不是“真正的”力，它是因为物体具有惯性和参考系加速运动而设想其存在的力，所以叫惯性力。质点受不受惯性力，取决于使用的参考系是惯性系还是非惯性系，与质点是否跟随非惯性系运动无关。
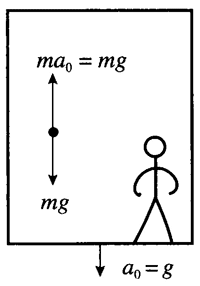
设想有一个电梯，其顶端的牵引钢索突然断掉，而且电梯中防止下滑的制动装置也同时失灵，而你恰好在电梯内，如图 4–12 所示，你会看到什么情景呢？这时电梯差不多是在做自由落体运动，或者说电梯在重力作用下自由降落，电梯自由降落的加速度为重力加速度 g。你在电梯内，会不自觉地以电梯为参考系，电梯是以重力加速度 g 加速下降的非惯性系，电梯内的物体除受向下的相互作用力，即重力 G = mg 之外，还要受向上的惯性力F = ma0 = mg 作用，二力大小相等、方向相反、互相抵消，因此你观察到电梯内的物体所受到的重力好像消失了一样，物体处于失重状态。因为你也在电梯内，所以你受到的重力也与惯性力抵消，你也处于失重状态，自由降落的电梯内形成了一个失重的环境。
当然，在自由降落的电梯内做实验太危险了。实际上，围绕地球做圆周运动的空间站就是在万有引力作用下的“自由降落”，只是空间站具有很大的切向速度而已。空间站内物体受到的惯性力正好与物体受到的万有引力大小相等、方向相反，因此空间站内物体所受的万有引力好像消失了一样，处于失重状态。可见，就像我国宇航员在神舟飞船上做的失重实验所反映的那样，在轨道上运行的空间站内也是一个失重的环境。
教科书中不涉及非惯性系问题，因此对失重现象有不同的讲法：一个人站在磅秤上，当人下蹲时会看到磅秤读数减小，这就是失重现象。这种讲法也是适当的，任何物体都可以作为参考系，所以可以用下蹲的人作为参考系，参考系具有向下的加速度，因此在这个参考系内物体都受到向上的惯性力。由于向上的惯性力抵消了一部分重力，所以人处于部分失重的状态。
6．测量火车运行时的加速度
火车出站后，在开始的一段时间内，基本做匀加速运动，正常运行中则是匀速运动。怎样测量火车运动时的加速度呢？可以用细线拴一个重物，通过细线与竖直方向的夹角计算火车的加速度。
取一个长方形纸板，按照图 4–13 所示，在纸板上画出标尺。用一段红色的细线拴一个重物作为指针，调整线的位置使线与标尺的竖直线重合后，把细线固定在 O 点。
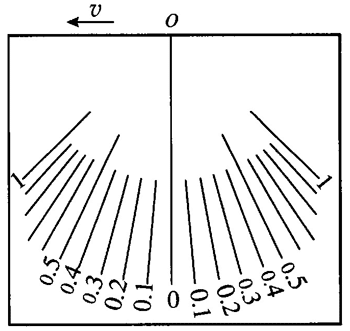
当火车做加速运动时，细线与竖直方向的夹角为 θ。则重物所受的合力 F = mgtanθ。根据牛顿第二定律，有 mgtanθ = ma。所以 a = gtanθ = g
除了火车，这种加速度测量计还适用于测虽水平运动的交通工具的加速度，特别是近似匀加速运动的交通工具。
7．用纸杯做失重实验
如图 4–14 所示，把两个金属螺母拴在一根橡皮筋的两端，再把橡皮筋的中点固定在纸杯底端正中，让螺母挂在纸杯的口边上。让纸杯从约 2 m 的高处自由下落，会发现螺母被橡皮筋拉回纸杯中并发出咔嚓的撞击声。
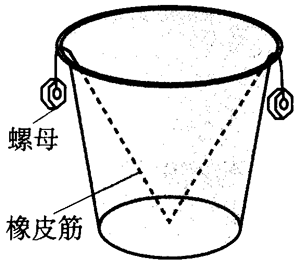
为什么下落后螺母会被拉入纸杯中？一开始，螺母受到重力和橡皮筋的拉力，所以橡皮筋处于拉伸状态。此时，纸杯受到重力、橡皮筋的拉力和手对纸杯向上的作用力。在刚放手时，橡皮筋仍处于拉伸状态，所以螺母受力不变，而纸杯受力不再平衡，因而向下加速运动。由于纸杯的运动，橡皮筋收缩，拉力减小，纸杯和螺母都向下加速运动，加速度不断变大。当螺母超过纸杯口后，橡皮筋对它拉力的方向就指向杯内。最后，纸杯和螺母都以重力加速度 g 自由下落，处于失重状态，橡皮筋拉力为 0，螺母被拉入纸杯中。
发布时间：2025/6/9 下午9:03:46 阅读次数：278
