二、光的干涉

我们在力学中学过了波的干涉，研究过水波和声波的干涉现象，我们知道，干涉是波特有的现象，只有频率相同、相差恒定的波源——相干波源才能产生稳定的干涉现象。对于水波或声波，相干波源是容易得到的，但是，要找到符合相干条件的两个相干光源却很困难。在室内点两支蜡烛或两盏电灯，只看到墙壁被均匀照亮，丝毫看不到光的干涉现象，当然，我们不应该因此就得出光不具有波动性的结论，因为这些光源都是独立发光的，甚至同一光源的两个发光部分，我们也无法使它们具有相同的频率和恒定的相差，所以，即使光具有波动性，这样的两个光源也不会产生稳定的干涉现象，无法看到干涉图样。

一、光的干涉

1801 年英国物理学家托马斯·杨（1773 ~ 1829）首先巧妙而简单地解决了相干光源的问题，成功地观察到了光的干涉现象。

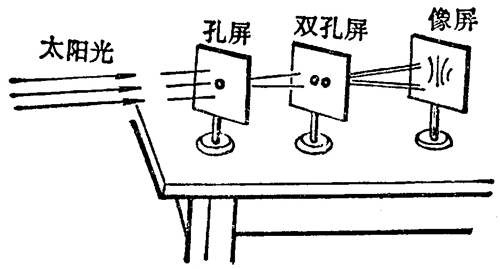
杨氏的办法是把点光源发出的一束光分成两束，以保证它们具有相同的频率和恒定的相差。实验做法如下，让太阳光照射到一个有小孔的屏上（图 6–1），这个小孔就成了一个“点光源”，光从小孔出来后，照射到第二个屏的两个小孔上，这两个小孔离得很近，而且与前一小孔的距离相等，因此，如果光是某种波动，那么任何时刻从前一小孔发出的光波都会同时传到这两个小孔，所以这两个小孔处的光振动不但频率相同，而且总是同相的。这两个小孔就成了两个相干光源，它们发出的光在像屏某处叠加时，如果同相，光就加强，如果反相，光就减弱或抵消，因此应该产生明暗条纹。实验果然产生了预期的结果，在像屏上看到了彩色的干涉条纹。

后来用狭缝代替小孔，用单色光代替太阳光来做实验，得到更清晰的明暗条纹，这就是著名的杨氏双缝干涉实验。图 6–2 是双缝干涉的装置和产生干涉图样的示意图。

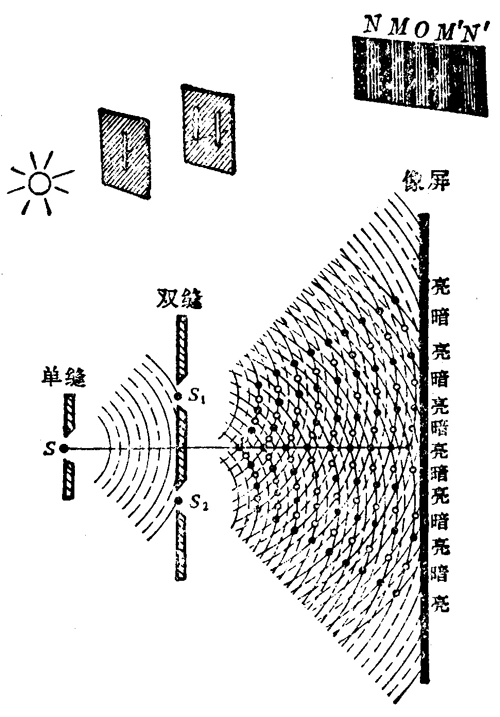
微粒说不能解释光的干涉现象，波动说则可以作出完善的解释，并能够根据双缝的距离和缝到屏的距离以及波长计算出屏上出现明暗条纹的位置。图 6–3 是用波动说研究双缝干涉的图，设两个缝 S₁ 和 S₂ 的距离为 d，到屏的距离为 l，且 l ≫ d。O 是 S₁S₂ 的中垂线与屏的交点，O 到 S₁、S₂ 的距离相等。从 S₁、S₂ 射出的光波到达 O 点经过的路程相等，所以两列波到达 O 点时相差为零，也就是说，是同相的，它们互相加强，在 O 点出现亮条纹，叫做中央亮纹，现在我们来研究离 O 点距离为 x 的 P 点的情况。P 到 S₁、S₂ 的距离分别为 r₁、r₂。从 S₁、S₂ 发出的光波到达 P 点的路程差是

$$\delta =r_2-r_1$$

从图中可以看出，

$$r_1^2=l^2+{\left(x-\frac{d}{2}\right)}^2,r_2^2=l^2+{\left(x+\frac{d}{2}\right)}^2$$

两式相减，可得

$$r_1^2-r_1^2=(r_2-r_1)(r_2+r_1)=2dx$$

由于 l ≫ d，且 l ≫ x，因此 r₂ + r₁ ≈ 2l，所以

$$\delta =\frac{d}{l}x$$

如果路程差 δ 等于波长 λ 的整数倍，两列波到达 P 点时同相，因而互相加强，这里就出现亮条纹；如果路程差 δ 等于半波长 λ/2 的奇数倍，两列波到达 P 点时反相，因而互相削弱，这里就出现暗条纹。所以，在屏上满足

$$x=\pm k\frac{l}{d}\lambda ,k=0,1,2,\cdots$$

的地方出现亮条纹。当 k = 0 时，x = 0 为中央亮纹；当 k = 1，2，……时，分别为中央亮纹两边的第 1 条、第 2 条……亮条纹。

在满足

$$x=\pm (2k-1)\frac{l}{d}\frac{\lambda }{2},k=0,1,2,\cdots$$

的地方出现暗条纹，当 k = 1，2，……时，分别为中央亮纹两边的第 1 条、第 2 条……暗条纹。

相邻两条亮纹（或暗纹）间的距离 ∆x 为

$$\mathrm{\Delta }x=\frac{l}{d}\lambda$$

可见，相邻两条亮纹（或暗纹）间的距离是相等的，从上式看出，在 d 和 λ 相同的情况下，干涉条纹间的距离 ∆x 跟波长 λ 有关系。用不同的色光做实验，可以看到 ∆x 的宽度不同，红光的最宽，紫光的最窄。这表明不同色光的波长不同，红光的波长最长，紫光的波长最短。用白光作光源时，由于各色光的波长不同，∆x 的宽度也不同，因此在中央白色亮纹两边出现彩色条纹。

上面的公式提供了一种测量光波波长的方法：测出 n 条亮纹（或暗纹）间的距离 a，算出相邻两条亮纹（或暗纹）间的距离 Δx = $\frac{a}{n-1}$，再测出 d 和 l 的值，就可以算出波长 λ。

二、波长和频率

我们知道，波长与频率的乘积等于波速。各种色光在真空中的速度都等于 c，如果用 ν 表示光波的频率；则有 c = λν。由于各种色光的波长不同，可见它们的频率也不相同。红光的波长最长，频率最小；紫光的波长最短，频率最大。下表是各种色光的频率和在真空中波长的范围：

光的波长也常用埃（Å）作单位，1 Å = 10⁻¹⁰m。但埃不是国际制单位。

发布时间：2025/6/7 下午9:00:01  阅读次数：298